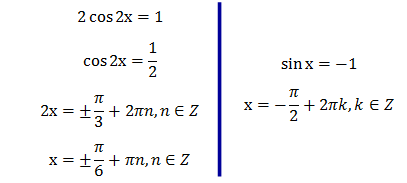Відмінності між версіями «Розв’язування тригонометричних рівнянь способом розкладання на множники»
(Створена сторінка: Тригонометричні рівняння) |
|||
| Рядок 1: | Рядок 1: | ||
| + | Багато тригонометричних рівнянь, права частина яких дорівнює 0, розв’язуються розкладанням їхньої лівої частини на множники. Під час розв’язування тригонометричних рівнянь цим способом усі члени рівняння переносять у ліву частину і подають утворений вираз у вигляді добутку. Далі використовують необхідну і достатню умови рівності нулю добутку тригонометричних виразів: добуток двох або кількох співмножників дорівнює нулю тоді і лише тоді, коли принаймні один зі співмножників дорівнює нулю, а інші при цьому не втрачають змісту. Розглянемо цей спосіб. | ||
| + | ''Приклад.'' | ||
| + | |||
| + | Розв’яжіть рівняння <math>2 sinx cos2x-1+2 cos2x-sinx=0</math>. | ||
| + | |||
| + | Розв’язання. Згрупуємо доданки у лівій частині рівняння: | ||
| + | |||
| + | <math>(2 sinx cos2x-sinx )+(2 cos2x-1)=0</math>. | ||
| + | |||
| + | <math>2 sinx cos2x-1+2 cos2x-sinx=0</math> | ||
| + | |||
| + | <math>(2cos2х-1)(sinх+1)=0 </math> | ||
| + | |||
| + | Враховуючи умову рівності нулю, маємо: | ||
| + | |||
| + | <math>2 cos2х-1=0</math> або <math>sinх+1=0</math>. | ||
| + | |||
| + | Кожне з цих рівнянь легко звести до найпростішого: | ||
| + | |||
| + | [[Файл:Триг.PNG]] | ||
| + | |||
| + | Відповідь: <math>х=±π/6+πn,n∈Z</math> ; | ||
| + | <math> х=-π/2+2πk,k∈Z</math> . | ||
[[Тригонометричні рівняння]] | [[Тригонометричні рівняння]] | ||
Поточна версія на 16:24, 24 квітня 2014
Багато тригонометричних рівнянь, права частина яких дорівнює 0, розв’язуються розкладанням їхньої лівої частини на множники. Під час розв’язування тригонометричних рівнянь цим способом усі члени рівняння переносять у ліву частину і подають утворений вираз у вигляді добутку. Далі використовують необхідну і достатню умови рівності нулю добутку тригонометричних виразів: добуток двох або кількох співмножників дорівнює нулю тоді і лише тоді, коли принаймні один зі співмножників дорівнює нулю, а інші при цьому не втрачають змісту. Розглянемо цей спосіб.
Приклад.
Розв’яжіть рівняння Неможливо розібрати вираз (невідома помилка): 2 sinx cos2x-1+2 cos2x-sinx=0 .
Розв’язання. Згрупуємо доданки у лівій частині рівняння:
Неможливо розібрати вираз (невідома помилка): (2 sinx cos2x-sinx )+(2 cos2x-1)=0 .
Неможливо розібрати вираз (невідома помилка): 2 sinx cos2x-1+2 cos2x-sinx=0
Неможливо розібрати вираз (невідома помилка): (2cos2х-1)(sinх+1)=0
Враховуючи умову рівності нулю, маємо:
Неможливо розібрати вираз (невідома помилка): 2 cos2х-1=0
або Неможливо розібрати вираз (невідома помилка): sinх+1=0
.
Кожне з цих рівнянь легко звести до найпростішого:
Відповідь: Неможливо розібрати вираз (невідома помилка): х=±π/6+πn,n∈Z
;
Неможливо розібрати вираз (невідома помилка): х=-π/2+2πk,k∈Z
.