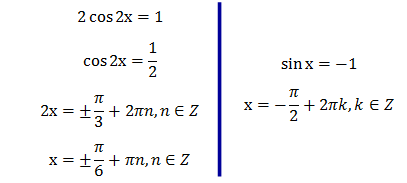Розв’язування тригонометричних рівнянь способом розкладання на множники

Багато тригонометричних рівнянь, права частина яких дорівнює 0, розв’язуються розкладанням їхньої лівої частини на множники. Під час розв’язування тригонометричних рівнянь цим способом усі члени рівняння переносять у ліву частину і подають утворений вираз у вигляді добутку. Далі використовують необхідну і достатню умови рівності нулю добутку тригонометричних виразів: добуток двох або кількох співмножників дорівнює нулю тоді і лише тоді, коли принаймні один зі співмножників дорівнює нулю, а інші при цьому не втрачають змісту. Розглянемо цей спосіб.

Приклад.

Розв’яжіть рівняння Неможливо розібрати вираз (невідома помилка): 2 sin⁡x cos⁡2x-1+2 cos⁡2x-sin⁡x=0 .

Розв’язання. Згрупуємо доданки у лівій частині рівняння:

Неможливо розібрати вираз (невідома помилка): (2 sin⁡x cos⁡2x-sin⁡x )+(2 cos⁡2x-1)=0 .

Неможливо розібрати вираз (невідома помилка): 2 sin⁡x cos⁡2x-1+2 cos⁡2x-sin⁡x=0

Неможливо розібрати вираз (невідома помилка): (2cos⁡2х-1)(sin⁡х+1)=0

Враховуючи умову рівності нулю, маємо:

Неможливо розібрати вираз (невідома помилка): 2 cos⁡2х-1=0

або  Неможливо розібрати вираз (невідома помилка): sin⁡х+1=0

.

Кожне з цих рівнянь легко звести до найпростішого:

Відповідь: Неможливо розібрати вираз (невідома помилка): х=±π/6+πn,n∈Z

;

Неможливо розібрати вираз (невідома помилка): х=-π/2+2πk,k∈Z

.

Тригонометричні рівняння