Відмінності між версіями «Комбінаторні методи. Метод гілок та меж»
| (не показані 4 проміжні версії цього учасника) | |||
| Рядок 1: | Рядок 1: | ||
| − | В основі комбінаторних методів є перебір можливих варіантів розв’язків поставленої задачі. Для розв’язування задач | + | == Комбінаторні методи == |
| + | |||
| + | В основі комбінаторних методів є перебір можливих варіантів розв’язків поставленої задачі. Для розв’язування задач цілочислового програмування ефективнішим за метод Гоморі є метод гілок і меж. Спочатку, як і в разі методу Гоморі, симплексним методом розв’язується послаблена (без умов цілочисловості) за-дача. Потім вводиться правило перебору. | ||
Нехай потрібно знайти <math>x_j</math> — цілочислову змінну, значення якої <math>x_j= x'_j</math> в оптимальному плані послабленої задачі є дробовим. Очевидно, що в деякому околі даної точки також не існує цілочислових значень, тому відповідний проміжок можна виключити з множини допустимих планів задачі в подальшому розгляді. Та-ким проміжком є інтервал між найближчими до <math>x'_j</math> цілочисловими значеннями. Можна стверджувати, що на інтервалі <math> \left [ \left [ x'_j \right ] ; \left [ x'_j \right ] + 1 \right ] </math>цілих значень немає. | Нехай потрібно знайти <math>x_j</math> — цілочислову змінну, значення якої <math>x_j= x'_j</math> в оптимальному плані послабленої задачі є дробовим. Очевидно, що в деякому околі даної точки також не існує цілочислових значень, тому відповідний проміжок можна виключити з множини допустимих планів задачі в подальшому розгляді. Та-ким проміжком є інтервал між найближчими до <math>x'_j</math> цілочисловими значеннями. Можна стверджувати, що на інтервалі <math> \left [ \left [ x'_j \right ] ; \left [ x'_j \right ] + 1 \right ] </math>цілих значень немає. | ||
| − | Наприклад, якщо <math>x'_j = 2,7</math> дістаємо інтервал \left [ 2;3 \right ] , де, очевидно, немає <math>x_j</math> , яке набуває цілого значення і оптимальний розв’язок буде знаходитися або в інтервалі <math>x_j \le 2</math>, або <math>x_j \ge 3</math> Виключення проміжку \left [ 2;3 \right ] з множини допустимих планів здійснюється введенням до системи обмежень початкової задачі додаткових | + | Наприклад, якщо <math>x'_j = 2,7</math> дістаємо інтервал <math>\left [ 2;3 \right ]</math> , де, очевидно, немає <math>x_j</math> , яке набуває цілого значення і оптимальний розв’язок буде знаходитися або в інтервалі <math>x_j \le 2</math>, або <math>x_j \ge 3</math> Виключення проміжку <math>\left [ 2;3 \right ]</math> з множини допустимих планів здійснюється введенням до системи обмежень початкової задачі додаткових нерівностей. Тобто допустиме ціле значення <math>x_j</math> має задовольняти одну з нерівностей виду: |
<math>x_j \le \left [ x'_j \right ]</math> або <math>x_j \ge \left [ x'_j \right ] +1</math> | <math>x_j \le \left [ x'_j \right ]</math> або <math>x_j \ge \left [ x'_j \right ] +1</math> | ||
| − | Дописавши кожну з цих умов до задачі з послабленими | + | Дописавши кожну з цих умов до задачі з послабленими обмеженнями, дістанемо дві, не пов’язані між собою, задачі. Тобто, [[Постановка_цілочислової_задачі_ЛП._Геометрична_інтерпретація | початкову задачу цілочислового програмування]] поділимо на дві задачі з урахуванням умов цілочисловості змінних, значення яких в оптимальному плані послабленої задачі є дробовими. |
Це означає, що симплекс-методом розв’язуватимемо дві такі задачі: | Це означає, що симплекс-методом розв’язуватимемо дві такі задачі: | ||
| Рядок 53: | Рядок 55: | ||
<center> <math>x_j \ge \left [ x'_j \right ] </math> '''(10)'''</center> | <center> <math>x_j \ge \left [ x'_j \right ] </math> '''(10)'''</center> | ||
| − | де <math>x'_j</math> — дробова компонента розв’язку початкової задачі цілочислового програмування. Наведені задачі (1)—(5) і (6)—(10) спочатку | + | де <math>x'_j</math> — дробова компонента розв’язку початкової задачі цілочислового програмування. Наведені задачі (1)—(5) і (6)—(10) спочатку послаблюємо, тобто розв’язуємо з відкиданням обмежень (4) і (9). Якщо знайдені оптимальні плани задовольняють умови цілочисловості, то ці плани є розв’язками початкової задачі цілочислового програмування. Інакше пошук розв’язку задачі триває. Для дальшого розгалуження вибираємо розв’язок задачі з більшим значенням цільової функції, якщо йдеться про максимізацію, і навпаки — з меншим значенням цільової функції в разі її мінімізації. Подальше розгалуження виконується доти, доки не буде встановлено неможливість поліпшення розв’язку. Здобутий останній план — оптимальний. |
| − | Розв’язування цілочислових задач методом гілок і меж можна значно прискорити. Очевидно, що кожна наступна задача, яку отримують в процесі розв’язування відрізняється від | + | Розв’язування цілочислових задач методом гілок і меж можна значно прискорити. Очевидно, що кожна наступна задача, яку отримують в процесі розв’язування відрізняється від попередньої лише одним обмеженням. Досить буде почергово приєднати нові обмеження виду (5) і (10) до останньої симплекс-таблиці попередньої задачі та вилучити (в разі необхідності) непотрібні «старі» обмеження. |
| + | |||
| + | Геометрично введення додаткових лінійних обмежень виду (5) та (10) в систему обмежень початкової задачі означає проведення гіперплощин (прямих), що розтинають багатогранник (багатокутник) допустимих планів відповідної задачі лінійного програмування у такий спосіб, що уможливлюється включення в план найближчої цілої точки цього багатокутника. | ||
| + | <center>[[Файл:Clip_image002.gif]]</center> Допустимо, що А — точка максимуму, тоді за методом гілок та меж багатокутник допустимих планів задачі ABCOD поділяється на дві частини прямими <math>x'_1 = \left [ x'_1 \right ]</math> та <math>x'_1 = \left [ x'_1 \right ]+1</math>, що виключає з розгляду точку А, координата якої <math>x'_1</math> є не цілим числом. | ||
| + | |||
| + | <center>[[Файл:Combmet.png]]</center> | ||
| + | |||
| + | |||
| + | == Алгоритм методу гілок та меж: == | ||
| + | |||
| + | Загальна цілочислова задача лінійного програмування записується так: | ||
| + | |||
| + | <center><math> \max \,(\min )\,\,F=\sum\limits_{j=1}^n {c_{j} x_{j} }</math> '''(1)'''</center> | ||
| + | за умов: | ||
| + | <center><math>\sum\limits_{j=1}^n {a_{ij} x_{j} } \left\{ {\begin{array}{l} | ||
| + | \le \\ | ||
| + | = \\ | ||
| + | \ge \\ | ||
| + | \end{array}} \right\}b_{i} | ||
| + | \quad | ||
| + | \left( {i=\overline {1,m} } \right);</math> '''(2)'''</center> | ||
| + | |||
| + | |||
| + | <center><math> | ||
| + | x_{j} \ge 0 | ||
| + | \quad | ||
| + | \left( {j=\overline {1,n} } \right);</math> '''(3)'''</center> | ||
| + | |||
| + | |||
| + | <center> <math>\ \quad x_{j}</math> - цілі числа <math>\left( {j=\overline {1,n} } \right);</math> '''(4)'''</center> | ||
| + | |||
| + | 1. Симплексним методом розв’язують задачу (1)—(3) (без вимог цілочисловості змінних). | ||
| + | |||
| + | Якщо серед елементів умовно-оптимального плану немає дробових чисел, то цей розв’язок є оптимальним планом задачі цілочислового програмування (1)—(4). | ||
| + | |||
| + | Якщо задача (1)—(3) не має розв’язку (цільова функція необмежена, або система обмежень несумісна), то задача (1)—(4) також не має розв’язку. | ||
| + | |||
| + | 2. Коли в умовно-оптимальному плані є дробові значення, то вибирають одну з нецілочислових змінних <math>x_i</math> і визначають її цілу частину <math> \left [ x'_i \right ]</math> | ||
| + | |||
| + | 3. Записують два обмеження, що відтинають нецілочислові розв’язки: | ||
| + | <center><math>x_i \le \left [ x'_i \right ] </math> </center> | ||
| + | <center><math>x_i \ge \left [ x'_i \right ] +1</math> </center> | ||
| + | 4. Кожну з одержаних нерівностей приєднують до обмежень початкової задачі. В результаті отримують дві нові цілочислові задачі лінійного програмування. | ||
| − | + | 5. У будь-якій послідовності розв’язують обидві задачі. | |
| + | У разі, коли отримано цілочисловий розв’язок хоча б однієї із задач, значення цільової функції цієї задачі зіставляють з початковим значенням. | ||
| + | Якщо різниця не більша від заданого числа <math>\epsilon</math>, то процес розв’язування може бути закінчено. | ||
| + | У разі, коли цілочисловий розв’язок одержано в обох задачах, то з розв’язком початкової зіставляється той, який дає краще значення цільової функції. | ||
| + | Якщо ж в обох задачах одержано нецілочислові розв’язки, то для дальшого гілкування вибирають ту задачу, для якої здобуто краще значення цільової функції і здійснюють перехід до кроку 2. | ||
Поточна версія на 11:24, 14 травня 2012
Комбінаторні методи
В основі комбінаторних методів є перебір можливих варіантів розв’язків поставленої задачі. Для розв’язування задач цілочислового програмування ефективнішим за метод Гоморі є метод гілок і меж. Спочатку, як і в разі методу Гоморі, симплексним методом розв’язується послаблена (без умов цілочисловості) за-дача. Потім вводиться правило перебору.
Нехай потрібно знайти Неможливо розібрати вираз (невідома помилка): x_j
— цілочислову змінну, значення якої Неможливо розібрати вираз (невідома помилка): x_j= x'_j в оптимальному плані послабленої задачі є дробовим. Очевидно, що в деякому околі даної точки також не існує цілочислових значень, тому відповідний проміжок можна виключити з множини допустимих планів задачі в подальшому розгляді. Та-ким проміжком є інтервал між найближчими до Неможливо розібрати вираз (невідома помилка): x'_j цілочисловими значеннями. Можна стверджувати, що на інтервалі Неможливо розібрати вираз (невідома помилка): \left [ \left [ x'_j \right ] ; \left [ x'_j \right ] + 1 \right ]
цілих значень немає.
Наприклад, якщо Неможливо розібрати вираз (невідома помилка): x'_j = 2,7
дістаємо інтервал Неможливо розібрати вираз (невідома помилка): \left [ 2;3 \right ] , де, очевидно, немає Неможливо розібрати вираз (невідома помилка): x_j , яке набуває цілого значення і оптимальний розв’язок буде знаходитися або в інтервалі Неможливо розібрати вираз (невідома помилка): x_j \le 2
, або Неможливо розібрати вираз (невідома помилка): x_j \ge 3
Виключення проміжку Неможливо розібрати вираз (невідома помилка): \left [ 2;3 \right ] з множини допустимих планів здійснюється введенням до системи обмежень початкової задачі додаткових нерівностей. Тобто допустиме ціле значення Неможливо розібрати вираз (невідома помилка): x_j має задовольняти одну з нерівностей виду:
Неможливо розібрати вираз (невідома помилка): x_j \le \left [ x'_j \right ]
або Неможливо розібрати вираз (невідома помилка): x_j \ge \left [ x'_j \right ] +1
Дописавши кожну з цих умов до задачі з послабленими обмеженнями, дістанемо дві, не пов’язані між собою, задачі. Тобто, початкову задачу цілочислового програмування поділимо на дві задачі з урахуванням умов цілочисловості змінних, значення яких в оптимальному плані послабленої задачі є дробовими.
Це означає, що симплекс-методом розв’язуватимемо дві такі задачі:
перша задача:
за умов:
- цілі числа Неможливо розібрати вираз (невідома помилка): \left( {j=\overline {1,n} } \right);
(4)друга задача:
за умов:
- цілі числа Неможливо розібрати вираз (невідома помилка): \left( {j=\overline {1,n} } \right);
(9)де Неможливо розібрати вираз (невідома помилка): x'_j
— дробова компонента розв’язку початкової задачі цілочислового програмування. Наведені задачі (1)—(5) і (6)—(10) спочатку послаблюємо, тобто розв’язуємо з відкиданням обмежень (4) і (9). Якщо знайдені оптимальні плани задовольняють умови цілочисловості, то ці плани є розв’язками початкової задачі цілочислового програмування. Інакше пошук розв’язку задачі триває. Для дальшого розгалуження вибираємо розв’язок задачі з більшим значенням цільової функції, якщо йдеться про максимізацію, і навпаки — з меншим значенням цільової функції в разі її мінімізації. Подальше розгалуження виконується доти, доки не буде встановлено неможливість поліпшення розв’язку. Здобутий останній план — оптимальний.
Розв’язування цілочислових задач методом гілок і меж можна значно прискорити. Очевидно, що кожна наступна задача, яку отримують в процесі розв’язування відрізняється від попередньої лише одним обмеженням. Досить буде почергово приєднати нові обмеження виду (5) і (10) до останньої симплекс-таблиці попередньої задачі та вилучити (в разі необхідності) непотрібні «старі» обмеження.
Геометрично введення додаткових лінійних обмежень виду (5) та (10) в систему обмежень початкової задачі означає проведення гіперплощин (прямих), що розтинають багатогранник (багатокутник) допустимих планів відповідної задачі лінійного програмування у такий спосіб, що уможливлюється включення в план найближчої цілої точки цього багатокутника.
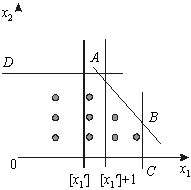
та Неможливо розібрати вираз (невідома помилка): x'_1 = \left [ x'_1 \right ]+1
, що виключає з розгляду точку А, координата якої Неможливо розібрати вираз (невідома помилка): x'_1
є не цілим числом.
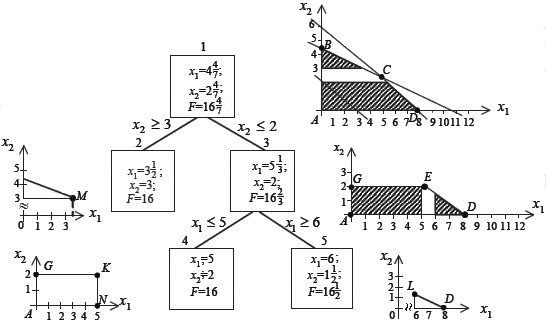
Алгоритм методу гілок та меж:
Загальна цілочислова задача лінійного програмування записується так:
за умов:
- цілі числа Неможливо розібрати вираз (невідома помилка): \left( {j=\overline {1,n} } \right);
(4)1. Симплексним методом розв’язують задачу (1)—(3) (без вимог цілочисловості змінних).
Якщо серед елементів умовно-оптимального плану немає дробових чисел, то цей розв’язок є оптимальним планом задачі цілочислового програмування (1)—(4).
Якщо задача (1)—(3) не має розв’язку (цільова функція необмежена, або система обмежень несумісна), то задача (1)—(4) також не має розв’язку.
2. Коли в умовно-оптимальному плані є дробові значення, то вибирають одну з нецілочислових змінних Неможливо розібрати вираз (невідома помилка): x_i
і визначають її цілу частину Неможливо розібрати вираз (невідома помилка): \left [ x'_i \right ]
3. Записують два обмеження, що відтинають нецілочислові розв’язки:
4. Кожну з одержаних нерівностей приєднують до обмежень початкової задачі. В результаті отримують дві нові цілочислові задачі лінійного програмування.
5. У будь-якій послідовності розв’язують обидві задачі. У разі, коли отримано цілочисловий розв’язок хоча б однієї із задач, значення цільової функції цієї задачі зіставляють з початковим значенням. Якщо різниця не більша від заданого числа Неможливо розібрати вираз (невідома помилка): \epsilon , то процес розв’язування може бути закінчено. У разі, коли цілочисловий розв’язок одержано в обох задачах, то з розв’язком початкової зіставляється той, який дає краще значення цільової функції. Якщо ж в обох задачах одержано нецілочислові розв’язки, то для дальшого гілкування вибирають ту задачу, для якої здобуто краще значення цільової функції і здійснюють перехід до кроку 2.
