Постановка цілочислової задачі ЛП. Геометрична інтерпретація

Економічна і математична постановка цілочислової задачі лінійного програмування

Існує доволі широке коло задач математичного програмування, в економіко-математичних моделях яких одна або кілька змінних мають набувати цілих значень. Наприклад, коли йдеться про кількість верстатів у цеху, тварин у сільськогосподарських підприємствах тощо. Зустрічаються також задачі, які з першого погляду не мають нічого спільного з цілочисловими моделями, проте формулюються як задачі цілочислового програмування. Вимоги дискретності змінних в явній чи неявній формах притаманні таким практичним задачам, як вибір послідовності виробничих процесів; календарне планування роботи підприємства; планування та забезпечення матеріально-технічного постачання, розміщення підприємств, розподіл капіталовкладень, планування використання обладнання тощо.

Задача математичного програмування, змінні якої мають набувати цілих значень, називається задачею цілочислового програмування. У тому разі, коли цілочислових значень мають набувати не всі, а одна чи кілька змінних, задача називається частково цілочисловою. До цілочислового програмування належать також ті задачі оптимізації, в яких змінні набувають лише двох значень: 0 або 1 (бульові, або бінарні змінні).

Умова цілочисловості є по суті нелінійною і може зустрічатися в задачах, що містять як лінійні, так і нелінійні функції. Розглянемо задачі математичного програмування, в яких крім умови цілочисловості всі обмеження та цільова функція є лінійними, що мають назву цілочислових задач лінійного програмування.

Загальна цілочислова задача лінійного програмування записується так:

Неможливо розібрати вираз (невідома помилка): \max \,(\min )\,\,F=\sum\limits_{j=1}^n {c_{j} x_{j} }

за умов:

Неможливо розібрати вираз (невідома помилка): \sum\limits_{j=1}^n {a_{ij} x_{j} } \left\{ {\begin{array}{l} \le \\ = \\ \ge \\ \end{array}} \right\}b_{i} \quad \left( {i=\overline {1,m} } \right);

Неможливо розібрати вираз (невідома помилка): x_{j} \ge 0 \quad \left( {j=\overline {1,n} } \right);

Неможливо розібрати вираз (невідома помилка): \ \quad x_{j}

- цілі числа  Неможливо розібрати вираз (невідома помилка): \left( {j=\overline {1,n} } \right);

Геометрична інтерпретація розв’язків цілочислових задач лінійного програмування на площині

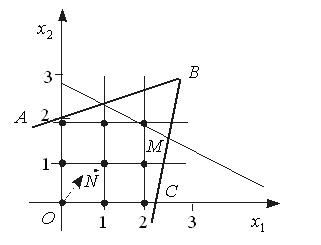
Для знаходження оптимального розв’язку цілочислових задач застосовують спеціальні методи. Найпростішим з них є знахо-дження оптимального розв’язку задачі як такої, що має лише не-перервні змінні, з дальшим їх округленням. Такий підхід є виправданим тоді, коли змінні в оптимальному плані набувають досить великих значень у зіставленні їх з одиницями вимірювання. Про-те за деяких умов такі спрощення призводять до істотних неточ-ностей. Скажімо, множина допустимих розв’язків деякої неціло-числової задачі лінійного програмування має вигляд, зображений на рис.1:

Рис.1

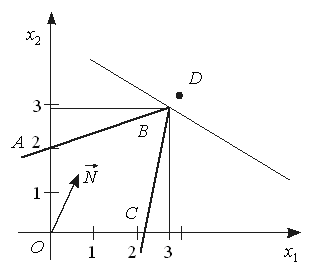
Максимальне значення функціонала для даної задачі знахо-диться в точці В. Округлення дасть таке значення оптимального плану Неможливо розібрати вираз (невідома помилка): x_{1} =3;\,\,\;x_{2} =3 (точка D на рис 1). Очевидно, що точка D не може бути розв’язком задачі, оскільки вона навіть не належить множині допустимих розв’язків

Геометрично множина допустимих планів будь-якої лінійної цілочислової задачі являє собою систему точок з цілочисловими координатами, що знаходяться всередині опуклого багатокутника допустимих розв’язків відповідної нецілочислової задачі.

Отже, для розглянутого на рис.1 випадку множина допустимих планів складається з дев’яти точок (рис.2), які утворені пере-тинами сім’ї прямих, що паралельні осям Ох1 та Oх2 і проходять через точки з цілими координатами 0, 1, 2. У нашому прикладі оптимальний цілочисловий розв’язок відповідає точці М Неможливо розібрати вираз (невідома помилка): x_{1} =2;\,\,\;x_{2} =2

Рис.2

Література

http://fingal.com.ua/content/view/479/76/1/0/

http://gendocs.ru/v13919/?cc=10