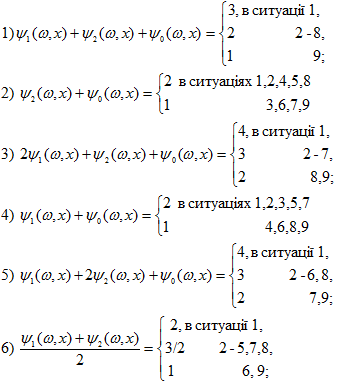Відмінності між версіями «Одноетапна Р-модель з імовірнісними обмеженнями. Алгоритм побудови розв’язувального правила. Приклад.»
9167465 (обговорення • внесок) |
|||
| (не показані 29 проміжних версій 2 учасників) | |||
| Рядок 1: | Рядок 1: | ||
| − | + | <font size=3> Потрібно визначити <math>x(\omega)</math>, максимізуючу ймовірність попадання в <math>G_0(\omega)</math> при умовах, що ймовірність попадання в <math>G_i(\omega), i=1,2,...,m</math>, не менше заданого числа <math>\alpha_i</math>. Таким чином, в самій постановці задачі припускається, що розв'язок визначається у вигляді випадкового вектора і розв'язувальне правило заздалегідь не задано. </font> | |
| − | < | + | <font size=3> Формально [[Одноетапна Р-модель з імовірнісними обмеженнями. Постановка задачі та умови сумісності.|задача]] записується у наступному вигляді: </font> |
| − | <math> P{x(\omega)\in | + | <font size=3> <math> P\{x(\omega)\in G_0(\omega)\}\rightarrow sup,</math> (4.1) </font> |
| + | <font size=3> <math> P\{x(\omega)\in G_i(\omega)\}\ge\alpha_i,i=1,2,...,m</math> (4.2) </font> | ||
| − | |||
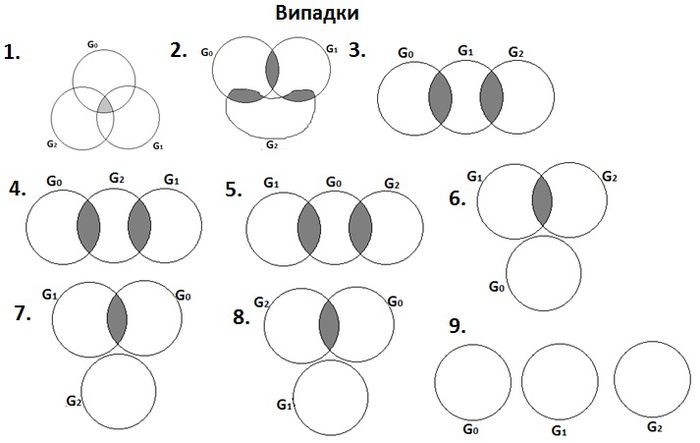
| − | + | <font size=3> Можна вказати наступні дев'ять попарно несумісних ситуацій взаємного розміщення множин <math> G_i, i=0,1,2,</math> які показують всі можливі випадки: </font> | |
| − | + | <font size=3> 1. <math> G_1\cap G_2 \cap G_0 \ne \varnothing,</math> </font> | |
| − | 3. <math> G_1\cap G_2 \cap G_0 = \varnothing, G_1\cap G_2 \ne \varnothing, | + | <font size=3> 2. <math> G_1\cap G_2 \cap G_0 = \varnothing, G_1\cap G_2 = \varnothing, G_1\cap G_0 \ne \varnothing, G_2\cap G_0 \ne \varnothing,</math> </font> |
| − | + | <font size=3> 3. <math> G_1\cap G_2 \cap G_0 = \varnothing, G_1\cap G_2 \ne \varnothing, G_1\cap G_0 \ne \varnothing, G_2\cap G_0 = \varnothing,</math> </font> | |
| − | + | <font size=3> 4. <math> G_1\cap G_2 \ne \varnothing, G_1\cap G_0 = \varnothing, G_2\cap G_0 \ne \varnothing,</math> </font> | |
| − | + | <font size=3> 5. <math> G_1\cap G_2 = \varnothing, G_1\cap G_0 \ne \varnothing, G_2\cap G_0 \ne \varnothing,</math> </font> | |
| − | + | <font size=3> 6. <math> G_1\cap G_2 = \varnothing, G_1\cap G_0 = \varnothing, G_2\cap G_0 = \varnothing,</math> </font> | |
| − | + | <font size=3> 7. <math> G_1\cap G_2 = \varnothing, G_1\cap G_0 \ne \varnothing, G_2\cap G_0 = \varnothing,</math> </font> | |
| − | + | <font size=3> 8. <math> G_1\cap G_2 = \varnothing, G_1\cap G_0 = \varnothing, G_2\cap G_0 \ne \varnothing,</math> </font> | |
| − | + | <font size=3> 9. <math> G_1\cap G_2 = G_1\cap G_0 = G_2\cap G_0 = \varnothing.</math> </font> | |
| − | + | [[Файл:JMDO.jpg|700px|thumb|right]] | |
| − | Розчленуємо множину <math> U=\bigcup\limits_{k=0}^2 G_k</math> на 7 підмножин, які попарно не перетинаються, наступним чином: | + | <font size=3> Нехай <math> \Omega_i</math> ‒ множина тих <math>\omega \in \Omega </math> при яких реалізується ''і''-та ситуація і <math> p_i=P\Omega_i, i=1,...,9.</math> </font> |
| + | |||
| + | <font size=3> Розчленуємо множину <math> U=\bigcup\limits_{k=0}^2 G_k</math> на 7 підмножин <math>U^j</math>, які попарно не перетинаються, наступним чином: </font> | ||
<math> U^1=G_0 \cap G_1 \cap G_2 ,</math> | <math> U^1=G_0 \cap G_1 \cap G_2 ,</math> | ||
| Рядок 44: | Рядок 46: | ||
<math> U^6=G_1 \setminus [(G_0\cap G_1)\cup (G_1 \cap G_2)] ,</math> | <math> U^6=G_1 \setminus [(G_0\cap G_1)\cup (G_1 \cap G_2)] ,</math> | ||
| − | <math> U^7=G_2 \setminus [(G_0\cap G_2)\cup (G_1 \cap G_2)] | + | <math> U^7=G_2 \setminus [(G_0\cap G_2)\cup (G_1 \cap G_2)] .</math> |
| − | Очевидно, що <math> U=\bigcup\limits_{j=0}^7 U^j; U^i \cap U^j = \varnothing</math> | + | <font size=3> Очевидно, що <math> U=\bigcup\limits_{j=0}^7 U^j; U^i \cap U^j = \varnothing</math> |
| − | <math> u_i^j | + | Введемо змінні <math> u_i^j</math>: </font> |
| − | <math> u_i^j | + | <math> u_i^j=P\{x\in U^j | i\}</math> |
| − | + | <font size=3> <math> u_i^j</math> - умовна ймовірність події <math> x \in U^j</math> за умови, що має місце ''і''-та ситуація взаємного розміщення множин <math> G_k</math>. </font> | |
| − | <math> | + | <font size=3> Мають місце співвідношення: <math> \sum^{T}_{j=1} u_i^j =1, i=1,...,9 </math>. Задача (4.1)-(4.2) еквівалентна наступній задачі лінійного програмування: </font> |
| − | <math> f(u)=\sum^{9}_{i=1} p_i(u_i^1+u_i^2+u_i^3+u_i^5) \rightarrow sup, </math> ( | + | <font size=3> <math> f(u)=\sum^{9}_{i=1} p_i(u_i^1+u_i^2+u_i^3+u_i^5) \rightarrow sup, </math> (3) </font> |
| − | <math> \sum^{9}_{i=1} p_i(u_i^1+u_i^2+u_i^4+u_i^6) \geqslant \alpha_1 </math> ( | + | <font size=3> <math> \sum^{9}_{i=1} p_i(u_i^1+u_i^2+u_i^4+u_i^6) \geqslant \alpha_1 </math> (4) </font> |
| − | <math> \sum^{9}_{i=1} p_i(u_i^1+u_i^3+u_i^4+u_i^7) \geqslant \alpha_2 </math> ( | + | <font size=3> <math> \sum^{9}_{i=1} p_i(u_i^1+u_i^3+u_i^4+u_i^7) \geqslant \alpha_2 </math> (5) </font> |
| − | <math> \sum^{9}_{i=1}u_i^j =1 , i=1,...9,</math> ( | + | <font size=3> <math> \sum^{9}_{i=1}u_i^j =1 , i=1,...9,</math> (6) </font> |
| − | <math> u_i^j \geqslant 0 , i=1,...9, j=1,...,7</math> . ( | + | <font size=3> <math> u_i^j \geqslant 0 , i=1,...9, j=1,...,7</math> . (7) </font> |
| − | Деякі зі змінних <math> u_i^j </math> для окремих ситуацій | + | <font size=3> Деякі зі змінних <math> u_i^j </math> для окремих ситуацій дорівнюють 0. Маємо: </font> |
| − | <math> \begin{cases} u_i^1=0, i=2,...,9, \\ u_i^2=0, i=4,6,8,9, \\ u_i^3=0, i=3,6,7,9,\\u_i^4=0, i=5,7,8,9 \end{cases} </math> | + | <font size=3> <math> \begin{cases} u_i^1=0, i=2,...,9, \\ u_i^2=0, i=4,6,8,9, \\ u_i^3=0, i=3,6,7,9,\\u_i^4=0, i=5,7,8,9 \end{cases} </math> (8) </font> |
| − | Побудуємо двоїсту задачу до задачі ( | + | <font size=3> Побудуємо двоїсту задачу до задачі (3)-(8): </font> |
| − | <math> g(\lambda)=-\alpha_1 \lambda_1 - \alpha_2\lambda_2+ \sum^{9}_{i=1}\lambda_{i+2} \rightarrow inf </math> ( | + | <font size=3> <math> g(\lambda)=-\alpha_1 \lambda_1 - \alpha_2\lambda_2+ \sum^{9}_{i=1}\lambda_{i+2} \rightarrow inf </math> (9) </font> |
| − | <math> \begin{cases} \lambda_{i+2}\geqslant\begin{cases} p_i(1+\lambda_1+\lambda_2), i=1,\\ p_i(1+\lambda_1+\lambda_2)-\lambda_i^1, i=2,...,9,\end{cases}\\ | + | <font size=3> <math> \begin{cases} \lambda_{i+2}\geqslant\begin{cases} p_i(1+\lambda_1+\lambda_2), i=1,\\ p_i(1+\lambda_1+\lambda_2)-\lambda_i^1, i=2,...,9,\end{cases}\\ |
\lambda_{i+2}\geqslant\begin{cases} p_i(1+\lambda_1), i=1,2,3,5,7,\\ p_i(1+\lambda_2)+\lambda_i^2, i=1,2,3,5,7,\end{cases}\\ | \lambda_{i+2}\geqslant\begin{cases} p_i(1+\lambda_1), i=1,2,3,5,7,\\ p_i(1+\lambda_2)+\lambda_i^2, i=1,2,3,5,7,\end{cases}\\ | ||
\lambda_{i+2}\geqslant\begin{cases} p_i(1+\lambda_2), i=1,2,3,5,7,\\ p_i(1+\lambda_2)-\lambda_i^3, i=3,6,7,9,\end{cases}\\ | \lambda_{i+2}\geqslant\begin{cases} p_i(1+\lambda_2), i=1,2,3,5,7,\\ p_i(1+\lambda_2)-\lambda_i^3, i=3,6,7,9,\end{cases}\\ | ||
| Рядок 82: | Рядок 84: | ||
\lambda_{i+2}\geqslant p_i\lambda_2, i=1,...,9, | \lambda_{i+2}\geqslant p_i\lambda_2, i=1,...,9, | ||
\end{cases} | \end{cases} | ||
| − | </math> ( | + | </math> (10) </font> |
| − | <math> \lambda_1 \geqslant 0,\lambda_2 \geqslant 0 </math> ( | + | <font size=3> <math> \lambda_1 \geqslant 0,\lambda_2 \geqslant 0 </math> (11) </font> |
| − | Тут двоїсті змінні <math> \lambda_1 ,\lambda_2 </math> відповідають обмеженням ( | + | <font size=3> Тут двоїсті змінні <math> \lambda_1 ,\lambda_2 </math> відповідають обмеженням (4) та (5) прямої задачі, змінні <math> \lambda_{i+2} (i=1,...,9) </math> відповідають умовам (6), а <math> \lambda_i^j(i=1,...,9, j=1,2,3,4)</math> - умовам (8). </font> |
| − | Позначимо через <math> \phi_i^k (\lambda_1, \lambda_2), (i=1,...,9; k=1,...7)</math> лінійні функції змінних <math> \lambda_1 ,\lambda_2 </math> які входять у праві частини умов ( | + | <font size=3> Позначимо через <math> \phi_i^k (\lambda_1, \lambda_2), (i=1,...,9; k=1,...7)</math> лінійні функції змінних <math> \lambda_1 ,\lambda_2 </math> які входять у праві частини умов (10), а через лінійні функції змінних <math> K(i)</math> - множину індексів, для яких відповідні умови із співвідношень (10) не містять змінних <math> \lambda_i^k</math>. Тоді нерівності (10) можна переписати у вигляді: </font> |
| − | <math> \lambda_{i+2}\geqslant \begin{cases}\phi_i^k, k\in K(i), \\ \phi_i^k - \lambda_i^k, k\notin K(i). \end{cases} </math> ( | + | <font size=3> <math> \lambda_{i+2}\geqslant \begin{cases}\phi_i^k, k\in K(i), \\ \phi_i^k - \lambda_i^k, k\notin K(i). \end{cases} </math> (12) </font> |
| − | Маємо наступні функції: | + | <font size=3> Маємо наступні функції: </font> |
| − | <math> \phi_i(\lambda_1,\lambda_2) = max_{k\in K(i)} {\phi_i^k (\lambda_1,\lambda_2)} </math> ( | + | <font size=3> <math> \phi_i(\lambda_1,\lambda_2) = max_{k\in K(i)} ({\phi_i^k (\lambda_1,\lambda_2)}) </math> (13) </font> |
| − | <math> \zeta_i(\lambda_1,\lambda_2, \lambda_i^k) = max_{k \in K(i)} {\phi_i^k (\lambda_1,\lambda_2) - \lambda_i^k } </math> ( | + | <font size=3> <math> \zeta_i(\lambda_1,\lambda_2, \lambda_i^k) = max_{k \in K(i)} ({\phi_i^k (\lambda_1,\lambda_2) - \lambda_i^k }) </math> (14) </font> |
| − | Тоді: | + | <font size=3> Тоді: </font> |
| − | <math> \ | + | <font size=3> <math> \lambda_{i+2} \geqslant max ({\phi_i, \zeta_i}) </math> (15) </font> |
| − | '''Лема 4.1.''' На оптимальному плані задачі ( | + | <font size=3> '''Лема 4.1.''' На оптимальному плані задачі (9)-(11) мають місце рівності </font> |
| − | <math> \ | + | <font size=3> <math> \lambda_{i+2} = \phi_i(\lambda_1,\lambda_2), (i=1,...,9) </math> (16) </font> |
| − | '''Теорема 4.2.''' Якщо умови задачі ( | + | <font size=3> '''Теорема 4.2.''' Якщо умови задачі (1)-(2) сумісні, то <math>supf(x)</math> за умов (4)-(7) дорівнює найменшому із семи чисел: </font> |
<math> S_1=(1-\alpha_1)+p_1-p_9, </math> | <math> S_1=(1-\alpha_1)+p_1-p_9, </math> | ||
| Рядок 119: | Рядок 121: | ||
<math> S_5=(1-\alpha_1)+2(1-\alpha_2)+p_1-p_7-p_9, </math> | <math> S_5=(1-\alpha_1)+2(1-\alpha_2)+p_1-p_7-p_9, </math> | ||
| − | <math> S_6={1 | + | <math> S_6=\frac{1}{2}[(1-\alpha_1)+(1-\alpha_2)+1-p_1-p_6-p_9], </math> |
| − | <math> S_7=1 </math> | + | <math> S_7=1. </math> |
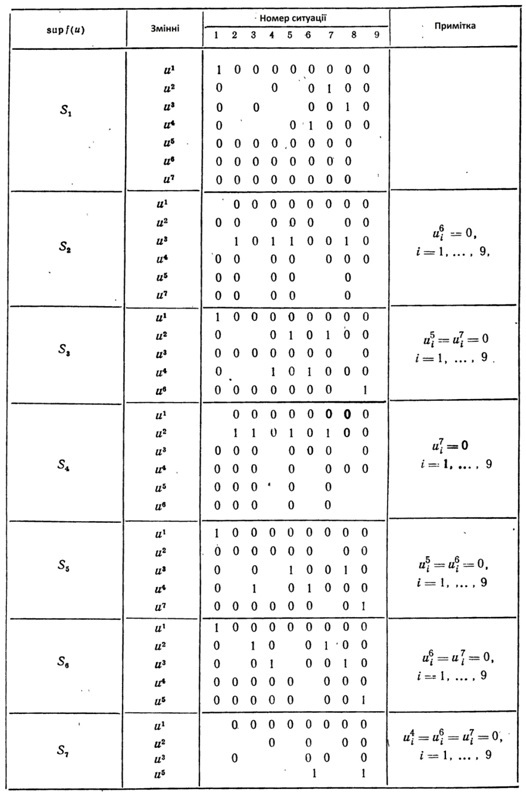
| − | [[Файл:YMDO2.jpg|600px|thumb|right]] | + | [[Файл:YMDO2.jpg|600px|thumb|right|Таблиця 1]] |
| − | Умова <math> f(u)-S_k </math> разом з обмеженнями ( | + | <font size=3> Умова <math> f(u)-S_k </math> разом з обмеженнями (10), (11) висікає множину оптимальних планів задачі. Для кожного набору параметрів умов задачі <math> (\alpha_1,\alpha_2,p_i) </math> оптимальні значення <math> u_i^j </math> належать одній із семи множин. Використовуючи другу теорему двоїстості лінійного програмування, можна виділити серед компонент розв'язку "вільні" та "закріплені". Таким чином отримаємо можливість, не розв'язуючи задачі, визначити оптимальні значення частини змінних, незалежно від реалізації випадкових параметрів умов задачі. Маючи на увазі, крім цього, співвідношення (8), отримаємо таблицю 1. </font> |
| − | Використовуючи таблицю | + | <font size=3> Використовуючи таблицю 1. можна спростити рівняння і нерівності, які визначають сім (по числу <math> S_k </math>) можливих багатогранних множин оптимальних планів задачі (3)-(7). Маємо: </font> |
| − | <math> \begin{cases} p_2(u_2^2+u_2^4)+ p_4 u_4^4+ p_5 u_5^2+ p_9 u_9^6 =\alpha_1 - p_1 - p_3 - p_6 - p_7,\\ p_2(u_2^2+u_2^4)+ p_4 u_3^4 + p_5 u_5^2+ p_9 u_9^6 =\alpha_2 - p_1 - p_4 - p_6 - p_8,\\ u_2^2 +u_2^3+u_2^4=1, u_3^2+u_3^4 =1, \\ u_4^3 +u_4^4=1, u_5^2+u_5^3 =1,\\ u_9^2 +u_9^6+u_9^7=1, u_i^j \geqslant 0 | + | <font size=3> <math> \begin{cases} p_2(u_2^2+u_2^4)+ p_4 u_4^4+ p_5 u_5^2+ p_9 u_9^6 =\alpha_1 - p_1 - p_3 - p_6 - p_7,\\ p_2(u_2^2+u_2^4)+ p_4 u_3^4 + p_5 u_5^2+ p_9 u_9^6 =\alpha_2 - p_1 - p_4 - p_6 - p_8,\\ u_2^2 +u_2^3+u_2^4=1, u_3^2+u_3^4 =1, \\ u_4^3 +u_4^4=1, u_5^2+u_5^3 =1,\\ u_9^2 +u_9^6+u_9^7=1, u_i^j \geqslant 0 |
| − | \end{cases}</math> ( | + | \end{cases}</math> (17) </font> |
| − | <math> \begin{cases} p_3(u_3^2+u_3^5)+ p_6 u_6^5+ p_7( u_7^2+u_7^5)+p_9 u_9^5 =1-\alpha_2,\\ p_2u_1^1+ p_3 (u_3^2 u_3^4)+ p_6 u_6^4 + p_7 u_7^2=\alpha_1 \\ u_1^1 +u_1^3=1, u_3^2+u_3^4 + u_3^5+u_3^7=1, \\ u_5^4 +u_6^5+u_6^7=1, u_7^2+u_7^5+u_7^7 =1,\\ u_5^9 +u_9^7=1, u_i^j \geqslant 0 | + | <font size=3> <math> \begin{cases} p_3(u_3^2+u_3^5)+ p_6 u_6^5+ p_7( u_7^2+u_7^5)+p_9 u_9^5 =1-\alpha_2,\\ p_2u_1^1+ p_3 (u_3^2 u_3^4)+ p_6 u_6^4 + p_7 u_7^2=\alpha_1 \\ u_1^1 +u_1^3=1, u_3^2+u_3^4 + u_3^5+u_3^7=1, \\ u_5^4 +u_6^5+u_6^7=1, u_7^2+u_7^5+u_7^7 =1,\\ u_5^9 +u_9^7=1, u_i^j \geqslant 0 |
| − | \end{cases}</math> ( | + | \end{cases}</math> (18) </font> |
| − | + | <font size=3> <math> \begin{cases} p_3 u_2^2+p_3 u_3^5= (1-\alpha_1)+(1-\alpha_2)- p_5 - p_7 - p_8 - p_9,\\ p_8u_8^3= 1-\alpha_1, p_8u_8^6= p_8-1+\alpha_1,\\ u_2^2 +u_2^4=1, u_3^2+u_3^4 =1, u_i^j \geqslant 0 | |
| + | \end{cases}</math> (19) </font> | ||
| − | + | <font size=3> <math> \begin{cases} p_4(u_3^4+u_4^5)+ p_6 u_6^5+ p_8( u_8^3+u_8^5)+p_9 u_9^5 =1-\alpha_1,\\ p_1u_1^1+ p_4 (u_4^3 u_4^4)+ p_6 u_6^4 + p_8 u_8^3\geqslant\alpha_2 \\ u_1^1 +u_1^2=1, u_4^3+u_4^4 + u_4^5+u_4^6=1, \\ u_6^4 +u_6^5+u_6^6=1, u_8^3+u_8^5+u_8^6 =1,\\ u_9^5 +u_9^6=1, u_i^j \geqslant 0 | |
| + | \end{cases}</math> (20) </font> | ||
| − | + | <font size=3> <math> \begin{cases} p_2 u_2^3+p_4 u_4^3= (1-\alpha_1)+(1-\alpha_2)- p_5 - p_7 - p_8 - p_9,\\ p_7u_7^2= 1-\alpha_2, p_7u_7^7= p_7-1+\alpha_2,\\ u_2^3 +u_2^4=1, u_4^3+u_4^4 =1, u_i^j \geqslant 0 | |
| + | \end{cases}</math> (21) </font> | ||
| − | '''Теорема 4.3.''' Якщо задача ( | + | <font size=3> <math> \begin{cases} p_2 u_2^2+p_5 u_5^2= \frac{1}{2}(\alpha_1-\alpha_2+ p_2 + p_4 - p_3 + p_5 - p_7 + p_8),\\ p_6u_6^4= \frac{1}{2}(\alpha_1+\alpha_2 -1 - p_1 + p_6 + p_9),\\ u_2^2 +u_2^3=1, u_5^2+u_5^3 =1, u_6^4+u_6^5 =1, u_i^j \geqslant 0 |
| + | \end{cases}</math> (22) </font> | ||
| + | |||
| + | <font size=3> <math> \begin{cases} p_1(u_1^1+u_1^2)+ p_2 u_2^2+ p_3 u_3^2+ p_5 u_5^2 + p_7 u_7^2 \geqslant\alpha_1,\\ p_1(u_1^1+u_1^3)+ p_2 u_2^3+ p_4 u_4^3+ p_5 u_5^3 + p_8 u_8^3 \geqslant\alpha_2,\\ u_1^1 +u_1^2+u_1^3+u_1^5=1, u_2^2+u_3^2+u_5^2 =1, \\ u_3^2+u_3^5=1, u_4^3+u_4^5 =1,\\ u_5^2 +u_5^3+u_5^5=1, \\ u_7^2+u_7^5=1, u_8^3+u_8^5 =1, u_i^j \geqslant 0 | ||
| + | \end{cases}</math> (23) </font> | ||
| + | |||
| + | <font size=3> Таким чином, маємо: </font> | ||
| + | |||
| + | <font size=3> '''Наслідок 4.2.''' Множина оптимальних планів задачі (3)-(7) визначається таблицею 1. та однією із систем (19)-(25) (в залежності від значень <math> \alpha_2, \alpha_1 </math> та <math> p_i </math>). </font> | ||
| + | |||
| + | <font size=3> '''Теорема 4.3.''' Якщо задача (1)-(2) сумісна, то існує ф-я <math> x^*(\omega) </math> яка є розв'язком задачі. При цьому, якщо верхня грань цільового функціонала <math> S(\alpha_1,\alpha_2)</math> дорівнює k-му числу <math> S_k </math> системи, яка визначається теоремою 4.2., тоді розв'язки задачі і тільки вони задовольняють умовам (4.2) та k-му рівнянню наступної системи: </font> | ||
[[Файл:Ymdo4.png|400px]] | [[Файл:Ymdo4.png|400px]] | ||
| − | '''Приклад.''' Розглянемо наступну задачу стохастичного програмування: | + | <font size=3> '''Приклад.''' Розглянемо наступну задачу стохастичного програмування: </font> |
| + | |||
| + | <font size=3> <math> P\{c(\omega) x(\omega) \geqslant L(\omega) \} \rightarrow sup,</math> (24) </font> | ||
| + | |||
| + | <font size=3> <math> \begin{cases} P\{A(\omega) x(\omega) \leqslant b(\omega) \} \geqslant \alpha_1,\\ P{x(\omega) \geqslant 0} \geqslant \alpha_2\end{cases}</math> (25) </font> | ||
| + | |||
| + | <font size=3> Припускається, що випадкова величина <math> L(\omega)</math> , всі компоненти випадкових векторів <math> c(\omega) i b(\omega)</math> та елементи випадкової матриці <math> A(\omega)</math> невід'ємні майже при всіх <math> \omega</math> Тоді з ймовірністю 1 множина <math> G_1 \cap G_2 \ne \varnothing </math>. (точка <math> x(\omega) </math> завжди належить <math> G_2 </math> та <math> G_2 </math>). </font> | ||
| + | |||
| + | <font size=3> Нехай крім цього <math>P \{ c(\omega) =0\}=0 </math>. Це означає, що <math> G_1 \cap G_2 \ne \varnothing </math> з ймовірністю 1. </font> | ||
| + | |||
| + | <font size=3> Таким чином, з 9 ситуацій з додатною ймовірністю з'язляються тільки три: 1, 2 та 4. Відповідно: </font> | ||
| + | |||
| + | <font size=3> <math> p_3=p_5=p_6=p_7=p_8=p_9=0 </math> (26) </font> | ||
| + | |||
| + | <font size=3> <math> p_1+p_2+p_4=1 </math> (27) </font> | ||
| + | |||
| + | <font size=3> Випишемо, враховуючи (26)-(27), можливі значення верхньої грані цільової функції задачі (1)-(2): </font> | ||
| + | |||
| + | <math> S_1=(1-\alpha_1)+(1-\alpha_2)+p_1, </math> | ||
| + | |||
| + | <math> S_2=(1-\alpha_2)+1, </math> | ||
| + | |||
| + | <math> S_3=2(1-\alpha_1)+(1-\alpha_2)+p_1, </math> | ||
| + | |||
| + | <math> S_4=(1-\alpha_1)+p_1+p_2, </math> | ||
| + | |||
| + | <math> S_5=(1-\alpha_1)+2(1-\alpha_2)+p_1, </math> | ||
| + | |||
| + | <math> S_6=\frac{1}{2}[(1-\alpha_1)+(1-\alpha_2)+p_1+1], </math> | ||
| + | |||
| + | <math> S_7=1. </math> | ||
| + | |||
| + | <font size=3> Очевидно, що <math> S_3\geqslant S_1, S_5 \geqslant S_1</math>. Крім цього, якщо <math> S_1 < 1</math> то <math> S_6 > S_1</math>. Якщо ж <math> S_1 \geqslant S_1</math> то <math> S_6 \geqslant S_1</math>.Отже, <math> S_2 \geqslant S_7</math>. Тобто оптимальне значення цільової функції задачі (1)-(2) може дорівнювати одному з 3-х чисел <math> S_1, S_4, S_7</math>. Розглянемо ці випадки послідовно: </font> | ||
| + | |||
| + | <font size=3> а) <math> S(\alpha_1,\alpha_2)=S_1= (1-\alpha_1)+(1-\alpha_2)+p_1</math>. </font> | ||
| + | |||
| + | <font size=3> <math> \begin{cases} p_2(u_2^2+u_2^4)+ p_4 u_4^4= \alpha_1-p_1,\\ p_2(u_2^3+u_2^4)= \alpha_2-1+p_2, \\ u_2^2 +u_2^3+u_2^4=1, u_3^2+u_3^4=1, u_4^3 +u_4^4=1,\\ u_5^2 +u_5^3=1, u_9^5 +u_9^6+u_9^7=1, u_i^j \geqslant 0 | ||
| + | \end{cases}</math> (28) </font> | ||
| + | |||
| + | <font size=3> Система (28) може бути переписана у вигляді: </font> | ||
| + | |||
| + | <font size=3> <math> \begin{cases} p_2u_2^3+p_4u_4^3= 1-\alpha_1,\\ p_2u_2^2= 1-\alpha_2, \\ u_2^2 +u_2^3+u_2^4=1, u_3^2+u_3^4=1, u_4^3 +u_4^4=1,\\ u_5^2 +u_5^3=1, u_9^5 +u_9^6+u_9^7=1, u_i^j \geqslant 0 | ||
| + | \end{cases}</math> (29) </font> | ||
| + | |||
| + | <font size=3> Розв’язок системи (29), взагалі кажучи, неоднозначний. </font> | ||
| + | |||
| + | <font size=3> б) <math> S(\alpha_1,\alpha_2)=S_4= 1-\alpha_1+p_1+p_2</math>. </font> | ||
| + | |||
| + | <font size=3> В цьому випадку множина розв’язків задачі задовольняє наступній системі співвідношень: </font> | ||
| + | |||
| + | <font size=3> <math> p_4(u_4^3+u_4^5)= 1-\alpha_1, </math> </font> | ||
| + | |||
| + | <font size=3> <math> p_1u_1^1+p_4(u_4^3+u_4^4)\geqslant\alpha_2, </math> </font> | ||
| + | |||
| + | <font size=3> <math> u_1^1 +u_1^2=1, u_4^3+u_4^4+u_4^5 +u_4^6=1, </math> </font> | ||
| + | |||
| + | <font size=3> <math> u_6^4 +u_6^5+u_6^6=1, u_8^3 +u_8^5+u_8^6=1, u_9^5+u_9^6=1, u_i^j \geqslant 0. </math> </font> | ||
| + | |||
| + | <font size=3> Умови <math> S_4\leqslant S </math> та <math> S_4\leqslant S_7 </math> мають вигляд: <math> \alpha_2\leqslant p_1+p_2 </math> </font> | ||
| + | |||
| + | <font size=3> в) <math> S(\alpha_1,\alpha_2)=S_7= 1.</math> </font> | ||
| + | |||
| + | <font size=3> В цьому випадку компоненти розв’язку задачі лінійного програмування, еквівалентної стохастичній задачі (1)-(2), задовольняють співвідношенням </font> | ||
| + | |||
| + | <font size=3> <math> p_1(u_1^1+u_1^2)+p_2u_2^2\geqslant\alpha_1, </math> </font> | ||
| + | |||
| + | <font size=3> <math> p_1(u_1^1+u_1^3)+p_2u_2^3+p_4u_4^3\geqslant\alpha_2, </math> </font> | ||
| + | |||
| + | <font size=3> <math> u_1^1 +u_1^2+u_1^3+u_1^5=1, u_2^2+u_2^3+u_2^5=1, u_3^2+u_3^5=1 </math> </font> | ||
| + | |||
| + | <font size=3> <math> u_4^3 +u_4^5=1, u_5^2 +u_5^3+u_5^5=1, u_7^2+u_7^5=1, u_8^3+u_8^5=1, u_i^j \geqslant 0. </math> </font> | ||
| + | |||
| + | <font size=3> Тут параметри умов задачі задовольняють нерівностям </font> | ||
| − | <math> | + | <font size=3> <math> a_1\leqslant p_1+p_2 (S_7\leqslant S_4), \alpha_1+\alpha_2+p_1\leqslant 1 (S_7\leqslant S_1). </math> </font> |
| − | < | + | <font size=3> Модель (1)-(2) не пов’язана з будь-якими припущеннями про характер областей <math> G_i </math>, або функцій, які їх породжують [1, c. 95-105]. </font> |
| − | |||
| − | |||
| − | + | ==Список використаних джерел== | |
| + | 1. Юдин Д. Б. Математические методы управления в условиях неполной информации. / Юдин Д. Б. М: «Сов. радио», 1974. – 400 с. | ||
| − | |||
| − | |||
| − | [[ | + | Виконала: [[Користувач:Маргаритка Дроздова|Маргарита Дроздова]] |
| − | + | Доповнювала: [[Користувач:Іванченко Дар’я|Іванченко Дар’я]] | |
| − | + | Доповнювала: [[Користувач:Поветкіна Олена|Повєткіна Олена]] | |
| − | [[ | + | Доповнював: [[Користувач:9167465|Білобабченко Анатолій]] |
Поточна версія на 23:18, 27 грудня 2020
Потрібно визначити Неможливо розібрати вираз (невідома помилка): x(\omega) , максимізуючу ймовірність попадання в Неможливо розібрати вираз (невідома помилка): G_0(\omega)
при умовах, що ймовірність попадання в Неможливо розібрати вираз (невідома помилка): G_i(\omega), i=1,2,...,m
, не менше заданого числа Неможливо розібрати вираз (невідома помилка): \alpha_i . Таким чином, в самій постановці задачі припускається, що розв'язок визначається у вигляді випадкового вектора і розв'язувальне правило заздалегідь не задано.
Формально задача записується у наступному вигляді:
Неможливо розібрати вираз (невідома помилка): P\{x(\omega)\in G_0(\omega)\}\rightarrow sup,
(4.1)
Неможливо розібрати вираз (невідома помилка): P\{x(\omega)\in G_i(\omega)\}\ge\alpha_i,i=1,2,...,m
(4.2)
Можна вказати наступні дев'ять попарно несумісних ситуацій взаємного розміщення множин Неможливо розібрати вираз (невідома помилка): G_i, i=0,1,2,
які показують всі можливі випадки:
1. Неможливо розібрати вираз (невідома помилка): G_1\cap G_2 \cap G_0 \ne \varnothing,
2. Неможливо розібрати вираз (невідома помилка): G_1\cap G_2 \cap G_0 = \varnothing, G_1\cap G_2 = \varnothing, G_1\cap G_0 \ne \varnothing, G_2\cap G_0 \ne \varnothing,
3. Неможливо розібрати вираз (невідома помилка): G_1\cap G_2 \cap G_0 = \varnothing, G_1\cap G_2 \ne \varnothing, G_1\cap G_0 \ne \varnothing, G_2\cap G_0 = \varnothing,
4. Неможливо розібрати вираз (невідома помилка): G_1\cap G_2 \ne \varnothing, G_1\cap G_0 = \varnothing, G_2\cap G_0 \ne \varnothing,
5. Неможливо розібрати вираз (невідома помилка): G_1\cap G_2 = \varnothing, G_1\cap G_0 \ne \varnothing, G_2\cap G_0 \ne \varnothing,
6. Неможливо розібрати вираз (невідома помилка): G_1\cap G_2 = \varnothing, G_1\cap G_0 = \varnothing, G_2\cap G_0 = \varnothing,
7. Неможливо розібрати вираз (невідома помилка): G_1\cap G_2 = \varnothing, G_1\cap G_0 \ne \varnothing, G_2\cap G_0 = \varnothing,
8. Неможливо розібрати вираз (невідома помилка): G_1\cap G_2 = \varnothing, G_1\cap G_0 = \varnothing, G_2\cap G_0 \ne \varnothing,
9. Неможливо розібрати вираз (невідома помилка): G_1\cap G_2 = G_1\cap G_0 = G_2\cap G_0 = \varnothing.
Нехай Неможливо розібрати вираз (невідома помилка): \Omega_i
‒ множина тих Неможливо розібрати вираз (невідома помилка): \omega \in \Omega при яких реалізується і-та ситуація і Неможливо розібрати вираз (невідома помилка): p_i=P\Omega_i, i=1,...,9.
Розчленуємо множину Неможливо розібрати вираз (невідома помилка): U=\bigcup\limits_{k=0}^2 G_k
на 7 підмножин Неможливо розібрати вираз (невідома помилка): U^j
, які попарно не перетинаються, наступним чином:
Неможливо розібрати вираз (невідома помилка): U^1=G_0 \cap G_1 \cap G_2 ,
Неможливо розібрати вираз (невідома помилка): U^2=(G_0 \cap G_1)\setminus G_0 \cap G_1\cap G_2 ,
Неможливо розібрати вираз (невідома помилка): U^3=(G_0 \cap G_2) \setminus G_0 \cap G_1\cap G_2 ,
Неможливо розібрати вираз (невідома помилка): U^4=(G_1 \cap G_2)\setminus G_0 \cap G_1\cap G_2 ,
Неможливо розібрати вираз (невідома помилка): U^5=G_0\setminus [(G_0\cap G_1)\cup (G_0 \cap G_2)] ,
Неможливо розібрати вираз (невідома помилка): U^6=G_1 \setminus [(G_0\cap G_1)\cup (G_1 \cap G_2)] ,
Неможливо розібрати вираз (невідома помилка): U^7=G_2 \setminus [(G_0\cap G_2)\cup (G_1 \cap G_2)] .
Очевидно, що Неможливо розібрати вираз (невідома помилка): U=\bigcup\limits_{j=0}^7 U^j; U^i \cap U^j = \varnothing
Введемо змінні Неможливо розібрати вираз (невідома помилка): u_i^j
Неможливо розібрати вираз (невідома помилка): u_i^j=P\{x\in U^j | i\}
Неможливо розібрати вираз (невідома помилка): u_i^j
- умовна ймовірність події Неможливо розібрати вираз (невідома помилка): x \in U^j за умови, що має місце і-та ситуація взаємного розміщення множин Неможливо розібрати вираз (невідома помилка): G_k
.
Мають місце співвідношення: Неможливо розібрати вираз (невідома помилка): \sum^{T}_{j=1} u_i^j =1, i=1,...,9 . Задача (4.1)-(4.2) еквівалентна наступній задачі лінійного програмування:
Неможливо розібрати вираз (невідома помилка): f(u)=\sum^{9}_{i=1} p_i(u_i^1+u_i^2+u_i^3+u_i^5) \rightarrow sup,
(3)
Неможливо розібрати вираз (невідома помилка): \sum^{9}_{i=1} p_i(u_i^1+u_i^2+u_i^4+u_i^6) \geqslant \alpha_1
(4)
Неможливо розібрати вираз (невідома помилка): \sum^{9}_{i=1} p_i(u_i^1+u_i^3+u_i^4+u_i^7) \geqslant \alpha_2
(5)
Неможливо розібрати вираз (невідома помилка): \sum^{9}_{i=1}u_i^j =1 , i=1,...9,
(6)
Неможливо розібрати вираз (невідома помилка): u_i^j \geqslant 0 , i=1,...9, j=1,...,7
. (7)
Деякі зі змінних Неможливо розібрати вираз (невідома помилка): u_i^j
для окремих ситуацій дорівнюють 0. Маємо:
Неможливо розібрати вираз (невідома помилка): \begin{cases} u_i^1=0, i=2,...,9, \\ u_i^2=0, i=4,6,8,9, \\ u_i^3=0, i=3,6,7,9,\\u_i^4=0, i=5,7,8,9 \end{cases}
(8)
Побудуємо двоїсту задачу до задачі (3)-(8):
Неможливо розібрати вираз (невідома помилка): g(\lambda)=-\alpha_1 \lambda_1 - \alpha_2\lambda_2+ \sum^{9}_{i=1}\lambda_{i+2} \rightarrow inf
(9)
Неможливо розібрати вираз (невідома помилка): \begin{cases} \lambda_{i+2}\geqslant\begin{cases} p_i(1+\lambda_1+\lambda_2), i=1,\\ p_i(1+\lambda_1+\lambda_2)-\lambda_i^1, i=2,...,9,\end{cases}\\ \lambda_{i+2}\geqslant\begin{cases} p_i(1+\lambda_1), i=1,2,3,5,7,\\ p_i(1+\lambda_2)+\lambda_i^2, i=1,2,3,5,7,\end{cases}\\ \lambda_{i+2}\geqslant\begin{cases} p_i(1+\lambda_2), i=1,2,3,5,7,\\ p_i(1+\lambda_2)-\lambda_i^3, i=3,6,7,9,\end{cases}\\ \lambda_{i+2}\geqslant\begin{cases} p_i(\lambda_1+\lambda_2), i=1,2,3,4,6,\\ p_i(\lambda_1+\lambda_2)-\lambda_i^4, i=5,7,8,9,\end{cases}\\ \lambda_{i+2}\geqslant p_i, i=1,...,9,\\ \lambda_{i+2}\geqslant p_i\lambda_1, i=1,...,9,\\ \lambda_{i+2}\geqslant p_i\lambda_2, i=1,...,9, \end{cases}
(10)
Неможливо розібрати вираз (невідома помилка): \lambda_1 \geqslant 0,\lambda_2 \geqslant 0
(11)
Тут двоїсті змінні Неможливо розібрати вираз (невідома помилка): \lambda_1 ,\lambda_2
відповідають обмеженням (4) та (5) прямої задачі, змінні Неможливо розібрати вираз (невідома помилка): \lambda_{i+2} (i=1,...,9)
відповідають умовам (6), а Неможливо розібрати вираз (невідома помилка): \lambda_i^j(i=1,...,9, j=1,2,3,4)
- умовам (8).
Позначимо через Неможливо розібрати вираз (невідома помилка): \phi_i^k (\lambda_1, \lambda_2), (i=1,...,9; k=1,...7)
лінійні функції змінних Неможливо розібрати вираз (невідома помилка): \lambda_1 ,\lambda_2 які входять у праві частини умов (10), а через лінійні функції змінних Неможливо розібрати вираз (невідома помилка): K(i) - множину індексів, для яких відповідні умови із співвідношень (10) не містять змінних Неможливо розібрати вираз (невідома помилка): \lambda_i^k
. Тоді нерівності (10) можна переписати у вигляді:
Неможливо розібрати вираз (невідома помилка): \lambda_{i+2}\geqslant \begin{cases}\phi_i^k, k\in K(i), \\ \phi_i^k - \lambda_i^k, k\notin K(i). \end{cases}
(12)
Маємо наступні функції:
Неможливо розібрати вираз (невідома помилка): \phi_i(\lambda_1,\lambda_2) = max_{k\in K(i)} ({\phi_i^k (\lambda_1,\lambda_2)})
(13)
Неможливо розібрати вираз (невідома помилка): \zeta_i(\lambda_1,\lambda_2, \lambda_i^k) = max_{k \in K(i)} ({\phi_i^k (\lambda_1,\lambda_2) - \lambda_i^k })
(14)
Тоді:
Неможливо розібрати вираз (невідома помилка): \lambda_{i+2} \geqslant max ({\phi_i, \zeta_i})
(15)
Лема 4.1. На оптимальному плані задачі (9)-(11) мають місце рівності
Неможливо розібрати вираз (невідома помилка): \lambda_{i+2} = \phi_i(\lambda_1,\lambda_2), (i=1,...,9)
(16)
Теорема 4.2. Якщо умови задачі (1)-(2) сумісні, то Неможливо розібрати вираз (невідома помилка): supf(x)
за умов (4)-(7) дорівнює найменшому із семи чисел:
Неможливо розібрати вираз (невідома помилка): S_1=(1-\alpha_1)+p_1-p_9,
Неможливо розібрати вираз (невідома помилка): S_2=(1-\alpha_2)+1-p_3-p_6-p_7-p_9,
Неможливо розібрати вираз (невідома помилка): S_3=2(1-\alpha_1)+(1-\alpha_2)+p_1-p_8-p_9,
Неможливо розібрати вираз (невідома помилка): S_4=(1-\alpha_1)+1-p_4-p_6-p_8-p_9,
Неможливо розібрати вираз (невідома помилка): S_5=(1-\alpha_1)+2(1-\alpha_2)+p_1-p_7-p_9,
Неможливо розібрати вираз (невідома помилка): S_6=\frac{1}{2}[(1-\alpha_1)+(1-\alpha_2)+1-p_1-p_6-p_9],
Неможливо розібрати вираз (невідома помилка): S_7=1.
Умова Неможливо розібрати вираз (невідома помилка): f(u)-S_k
разом з обмеженнями (10), (11) висікає множину оптимальних планів задачі. Для кожного набору параметрів умов задачі Неможливо розібрати вираз (невідома помилка): (\alpha_1,\alpha_2,p_i) оптимальні значення Неможливо розібрати вираз (невідома помилка): u_i^j належать одній із семи множин. Використовуючи другу теорему двоїстості лінійного програмування, можна виділити серед компонент розв'язку "вільні" та "закріплені". Таким чином отримаємо можливість, не розв'язуючи задачі, визначити оптимальні значення частини змінних, незалежно від реалізації випадкових параметрів умов задачі. Маючи на увазі, крім цього, співвідношення (8), отримаємо таблицю 1.
Використовуючи таблицю 1. можна спростити рівняння і нерівності, які визначають сім (по числу Неможливо розібрати вираз (невідома помилка): S_k ) можливих багатогранних множин оптимальних планів задачі (3)-(7). Маємо:
Неможливо розібрати вираз (невідома помилка): \begin{cases} p_2(u_2^2+u_2^4)+ p_4 u_4^4+ p_5 u_5^2+ p_9 u_9^6 =\alpha_1 - p_1 - p_3 - p_6 - p_7,\\ p_2(u_2^2+u_2^4)+ p_4 u_3^4 + p_5 u_5^2+ p_9 u_9^6 =\alpha_2 - p_1 - p_4 - p_6 - p_8,\\ u_2^2 +u_2^3+u_2^4=1, u_3^2+u_3^4 =1, \\ u_4^3 +u_4^4=1, u_5^2+u_5^3 =1,\\ u_9^2 +u_9^6+u_9^7=1, u_i^j \geqslant 0 \end{cases}
(17)
Неможливо розібрати вираз (невідома помилка): \begin{cases} p_3(u_3^2+u_3^5)+ p_6 u_6^5+ p_7( u_7^2+u_7^5)+p_9 u_9^5 =1-\alpha_2,\\ p_2u_1^1+ p_3 (u_3^2 u_3^4)+ p_6 u_6^4 + p_7 u_7^2=\alpha_1 \\ u_1^1 +u_1^3=1, u_3^2+u_3^4 + u_3^5+u_3^7=1, \\ u_5^4 +u_6^5+u_6^7=1, u_7^2+u_7^5+u_7^7 =1,\\ u_5^9 +u_9^7=1, u_i^j \geqslant 0 \end{cases}
(18)
Неможливо розібрати вираз (невідома помилка): \begin{cases} p_3 u_2^2+p_3 u_3^5= (1-\alpha_1)+(1-\alpha_2)- p_5 - p_7 - p_8 - p_9,\\ p_8u_8^3= 1-\alpha_1, p_8u_8^6= p_8-1+\alpha_1,\\ u_2^2 +u_2^4=1, u_3^2+u_3^4 =1, u_i^j \geqslant 0 \end{cases}
(19)
Неможливо розібрати вираз (невідома помилка): \begin{cases} p_4(u_3^4+u_4^5)+ p_6 u_6^5+ p_8( u_8^3+u_8^5)+p_9 u_9^5 =1-\alpha_1,\\ p_1u_1^1+ p_4 (u_4^3 u_4^4)+ p_6 u_6^4 + p_8 u_8^3\geqslant\alpha_2 \\ u_1^1 +u_1^2=1, u_4^3+u_4^4 + u_4^5+u_4^6=1, \\ u_6^4 +u_6^5+u_6^6=1, u_8^3+u_8^5+u_8^6 =1,\\ u_9^5 +u_9^6=1, u_i^j \geqslant 0 \end{cases}
(20)
Неможливо розібрати вираз (невідома помилка): \begin{cases} p_2 u_2^3+p_4 u_4^3= (1-\alpha_1)+(1-\alpha_2)- p_5 - p_7 - p_8 - p_9,\\ p_7u_7^2= 1-\alpha_2, p_7u_7^7= p_7-1+\alpha_2,\\ u_2^3 +u_2^4=1, u_4^3+u_4^4 =1, u_i^j \geqslant 0 \end{cases}
(21)
Неможливо розібрати вираз (невідома помилка): \begin{cases} p_2 u_2^2+p_5 u_5^2= \frac{1}{2}(\alpha_1-\alpha_2+ p_2 + p_4 - p_3 + p_5 - p_7 + p_8),\\ p_6u_6^4= \frac{1}{2}(\alpha_1+\alpha_2 -1 - p_1 + p_6 + p_9),\\ u_2^2 +u_2^3=1, u_5^2+u_5^3 =1, u_6^4+u_6^5 =1, u_i^j \geqslant 0 \end{cases}
(22)
Неможливо розібрати вираз (невідома помилка): \begin{cases} p_1(u_1^1+u_1^2)+ p_2 u_2^2+ p_3 u_3^2+ p_5 u_5^2 + p_7 u_7^2 \geqslant\alpha_1,\\ p_1(u_1^1+u_1^3)+ p_2 u_2^3+ p_4 u_4^3+ p_5 u_5^3 + p_8 u_8^3 \geqslant\alpha_2,\\ u_1^1 +u_1^2+u_1^3+u_1^5=1, u_2^2+u_3^2+u_5^2 =1, \\ u_3^2+u_3^5=1, u_4^3+u_4^5 =1,\\ u_5^2 +u_5^3+u_5^5=1, \\ u_7^2+u_7^5=1, u_8^3+u_8^5 =1, u_i^j \geqslant 0 \end{cases}
(23)
Таким чином, маємо:
Наслідок 4.2. Множина оптимальних планів задачі (3)-(7) визначається таблицею 1. та однією із систем (19)-(25) (в залежності від значень Неможливо розібрати вираз (невідома помилка): \alpha_2, \alpha_1
та Неможливо розібрати вираз (невідома помилка): p_i
).
Теорема 4.3. Якщо задача (1)-(2) сумісна, то існує ф-я Неможливо розібрати вираз (невідома помилка): x^*(\omega)
яка є розв'язком задачі. При цьому, якщо верхня грань цільового функціонала Неможливо розібрати вираз (невідома помилка): S(\alpha_1,\alpha_2) дорівнює k-му числу Неможливо розібрати вираз (невідома помилка): S_k системи, яка визначається теоремою 4.2., тоді розв'язки задачі і тільки вони задовольняють умовам (4.2) та k-му рівнянню наступної системи:
Приклад. Розглянемо наступну задачу стохастичного програмування:
Неможливо розібрати вираз (невідома помилка): P\{c(\omega) x(\omega) \geqslant L(\omega) \} \rightarrow sup,
(24)
Неможливо розібрати вираз (невідома помилка): \begin{cases} P\{A(\omega) x(\omega) \leqslant b(\omega) \} \geqslant \alpha_1,\\ P{x(\omega) \geqslant 0} \geqslant \alpha_2\end{cases}
(25)
Припускається, що випадкова величина Неможливо розібрати вираз (невідома помилка): L(\omega)
, всі компоненти випадкових векторів Неможливо розібрати вираз (невідома помилка): c(\omega) i b(\omega) та елементи випадкової матриці Неможливо розібрати вираз (невідома помилка): A(\omega) невід'ємні майже при всіх Неможливо розібрати вираз (невідома помилка): \omega Тоді з ймовірністю 1 множина Неможливо розібрати вираз (невідома помилка): G_1 \cap G_2 \ne \varnothing
. (точка Неможливо розібрати вираз (невідома помилка): x(\omega)
завжди належить Неможливо розібрати вираз (невідома помилка): G_2 та Неможливо розібрати вираз (невідома помилка): G_2
).
Нехай крім цього Неможливо розібрати вираз (невідома помилка): P \{ c(\omega) =0\}=0 . Це означає, що Неможливо розібрати вираз (невідома помилка): G_1 \cap G_2 \ne \varnothing
з ймовірністю 1.
Таким чином, з 9 ситуацій з додатною ймовірністю з'язляються тільки три: 1, 2 та 4. Відповідно:
Неможливо розібрати вираз (невідома помилка): p_3=p_5=p_6=p_7=p_8=p_9=0
(26)
Неможливо розібрати вираз (невідома помилка): p_1+p_2+p_4=1
(27)
Випишемо, враховуючи (26)-(27), можливі значення верхньої грані цільової функції задачі (1)-(2):
Неможливо розібрати вираз (невідома помилка): S_1=(1-\alpha_1)+(1-\alpha_2)+p_1,
Неможливо розібрати вираз (невідома помилка): S_2=(1-\alpha_2)+1,
Неможливо розібрати вираз (невідома помилка): S_3=2(1-\alpha_1)+(1-\alpha_2)+p_1,
Неможливо розібрати вираз (невідома помилка): S_4=(1-\alpha_1)+p_1+p_2,
Неможливо розібрати вираз (невідома помилка): S_5=(1-\alpha_1)+2(1-\alpha_2)+p_1,
Неможливо розібрати вираз (невідома помилка): S_6=\frac{1}{2}[(1-\alpha_1)+(1-\alpha_2)+p_1+1],
Неможливо розібрати вираз (невідома помилка): S_7=1.
Очевидно, що Неможливо розібрати вираз (невідома помилка): S_3\geqslant S_1, S_5 \geqslant S_1
. Крім цього, якщо Неможливо розібрати вираз (невідома помилка): S_1 < 1
то Неможливо розібрати вираз (невідома помилка): S_6 > S_1
. Якщо ж Неможливо розібрати вираз (невідома помилка): S_1 \geqslant S_1
то Неможливо розібрати вираз (невідома помилка): S_6 \geqslant S_1
.Отже, Неможливо розібрати вираз (невідома помилка): S_2 \geqslant S_7 . Тобто оптимальне значення цільової функції задачі (1)-(2) може дорівнювати одному з 3-х чисел Неможливо розібрати вираз (невідома помилка): S_1, S_4, S_7 . Розглянемо ці випадки послідовно:
а) Неможливо розібрати вираз (невідома помилка): S(\alpha_1,\alpha_2)=S_1= (1-\alpha_1)+(1-\alpha_2)+p_1 .
Неможливо розібрати вираз (невідома помилка): \begin{cases} p_2(u_2^2+u_2^4)+ p_4 u_4^4= \alpha_1-p_1,\\ p_2(u_2^3+u_2^4)= \alpha_2-1+p_2, \\ u_2^2 +u_2^3+u_2^4=1, u_3^2+u_3^4=1, u_4^3 +u_4^4=1,\\ u_5^2 +u_5^3=1, u_9^5 +u_9^6+u_9^7=1, u_i^j \geqslant 0 \end{cases}
(28)
Система (28) може бути переписана у вигляді:
Неможливо розібрати вираз (невідома помилка): \begin{cases} p_2u_2^3+p_4u_4^3= 1-\alpha_1,\\ p_2u_2^2= 1-\alpha_2, \\ u_2^2 +u_2^3+u_2^4=1, u_3^2+u_3^4=1, u_4^3 +u_4^4=1,\\ u_5^2 +u_5^3=1, u_9^5 +u_9^6+u_9^7=1, u_i^j \geqslant 0 \end{cases}
(29)
Розв’язок системи (29), взагалі кажучи, неоднозначний.
б) Неможливо розібрати вираз (невідома помилка): S(\alpha_1,\alpha_2)=S_4= 1-\alpha_1+p_1+p_2 .
В цьому випадку множина розв’язків задачі задовольняє наступній системі співвідношень:
Неможливо розібрати вираз (невідома помилка): p_4(u_4^3+u_4^5)= 1-\alpha_1,
Неможливо розібрати вираз (невідома помилка): p_1u_1^1+p_4(u_4^3+u_4^4)\geqslant\alpha_2,
Неможливо розібрати вираз (невідома помилка): u_1^1 +u_1^2=1, u_4^3+u_4^4+u_4^5 +u_4^6=1,
Неможливо розібрати вираз (невідома помилка): u_6^4 +u_6^5+u_6^6=1, u_8^3 +u_8^5+u_8^6=1, u_9^5+u_9^6=1, u_i^j \geqslant 0.
Умови Неможливо розібрати вираз (невідома помилка): S_4\leqslant S
та Неможливо розібрати вираз (невідома помилка): S_4\leqslant S_7 мають вигляд: Неможливо розібрати вираз (невідома помилка): \alpha_2\leqslant p_1+p_2
в) Неможливо розібрати вираз (невідома помилка): S(\alpha_1,\alpha_2)=S_7= 1.
В цьому випадку компоненти розв’язку задачі лінійного програмування, еквівалентної стохастичній задачі (1)-(2), задовольняють співвідношенням
Неможливо розібрати вираз (невідома помилка): p_1(u_1^1+u_1^2)+p_2u_2^2\geqslant\alpha_1,
Неможливо розібрати вираз (невідома помилка): p_1(u_1^1+u_1^3)+p_2u_2^3+p_4u_4^3\geqslant\alpha_2,
Неможливо розібрати вираз (невідома помилка): u_1^1 +u_1^2+u_1^3+u_1^5=1, u_2^2+u_2^3+u_2^5=1, u_3^2+u_3^5=1
Неможливо розібрати вираз (невідома помилка): u_4^3 +u_4^5=1, u_5^2 +u_5^3+u_5^5=1, u_7^2+u_7^5=1, u_8^3+u_8^5=1, u_i^j \geqslant 0.
Тут параметри умов задачі задовольняють нерівностям
Неможливо розібрати вираз (невідома помилка): a_1\leqslant p_1+p_2 (S_7\leqslant S_4), \alpha_1+\alpha_2+p_1\leqslant 1 (S_7\leqslant S_1).
Модель (1)-(2) не пов’язана з будь-якими припущеннями про характер областей Неможливо розібрати вираз (невідома помилка): G_i , або функцій, які їх породжують [1, c. 95-105].
Список використаних джерел
1. Юдин Д. Б. Математические методы управления в условиях неполной информации. / Юдин Д. Б. М: «Сов. радио», 1974. – 400 с.
Виконала: Маргарита Дроздова
Доповнювала: Іванченко Дар’я
Доповнювала: Повєткіна Олена
Доповнював: Білобабченко Анатолій