Відмінності між версіями «Графічний метод для задач ЛП N-вимірного простору при N більше 3»

Версія за 15:29, 4 травня 2012

Розв'язувати графічним методом можна також задачі лінійного програмування n-вимірного простору, де n>3 , якщо при зведенні системи нерівностей задачі до системи рівнянь шляхом введення додаткових змінних кількість змінних n на дві більша, ніж число обмежень m, тобто n-m=2.

Тоді, як відомо з курсу вищої математики, можна дві з n змінних, наприклад Неможливо розібрати вираз (невідома помилка): X_1

та Неможливо розібрати вираз (невідома помилка):  X_2 

, вибрати як вільні, а інші m зробити базисними і виразити через вільні. Припустимо, що це зроблено. Отримаємо n-m=2 рівнянь вигляду:

Оскільки всі значення Неможливо розібрати вираз (невідома помилка): x_{i} \ge 0\;\,\,\,(i=\overline {1,n} )

то мають виконуватись умови:

Розглянемо, як можна зобразити ці умови геометрично. Візьмемо, наприклад, першу з них:

Узявши величину Неможливо розібрати вираз (невідома помилка): x_{3}

рівною своєму крайньому значенню — нулю, отримаємо рівняння: Неможливо розібрати вираз (невідома помилка): a_{31}x_{1}+a_{32}x_{2}+\beta_{3}=0.

Це рівняння прямої. Для такої прямої Неможливо розібрати вираз (невідома помилка): x_{3}=0

, по одну сторону від неї Неможливо розібрати вираз (невідома помилка): x_{3}>0
, а по другу — Неможливо розібрати вираз (невідома помилка): x_{3}<0

. Відмітимо ту сторону прямої Неможливо розібрати вираз (невідома помилка): a_{31}x_{1}+a_{32}x_{2}+\beta_{3}=0

, де Неможливо розібрати вираз (невідома помилка): x_{3}<0

. В аналогічний спосіб побудуємо і всі інші обмежуючі прямі: Неможливо розібрати вираз (невідома помилка): x_{4}=0; x_{5}=0 ... x_{n}=0

і відмітимо для кожної з них півплощину, де відповідна змінна більше нуля.

У такий спосіб отримують n – 2 прямі та дві осі координат Неможливо розібрати вираз (невідома помилка): (x_{1}=0, x_{2}=0) . Кожна з них визначає півплощину, де виконується умова Неможливо розібрати вираз (невідома помилка): x_{i}>0\, (i=\overline {1,n-2} ) . Частина площини в Неможливо розібрати вираз (невідома помилка): x_{1}Ox_{2}

належить водночас всім півплощинам, утворюючи багатокутник допустимих розв’язків.

Припустимо, що в задачі необхідно знайти максимальне значення функціонала:

Підставивши вирази для Неможливо розібрати вираз (невідома помилка): x_{3},\, x_{4}, \, x_{5} ... \, x_{n}

з (1) у цей функціонал, зведемо подібні доданки і отримаємо вираз лінійної функції F всіх n змінних лише через дві вільні змінні Неможливо розібрати вираз (невідома помилка):  X_1 
та Неможливо розібрати вираз (невідома помилка):  X_2 

Неможливо розібрати вираз (невідома помилка): F=y_{0}+y_{1}x_{1}+y_{2}x_{2}

, де Неможливо розібрати вираз (невідома помилка): Y_0

— вільний член, якого в початковому вигляді функціонала не було. Очевидно, що лінійна функція  Неможливо розібрати вираз (невідома помилка): F^{'}=y_{1}x_{1}+y_{2}x_{2}\, \, \,
досягає свого максимального значення за тих самих значень Неможливо розібрати вираз (невідома помилка):  X_1 
та Неможливо розібрати вираз (невідома помилка):  X_2 
, що й  Неможливо розібрати вираз (невідома помилка): F=y_{0}+y_{1}x_{1}+y_{2}x_{2}

. Отже, процедура відшукання оптимального плану з множини допустимих далі здійснюється за алгоритмом для випадку двох змінних.

Приклад

Розв’язати графічним методом задачу лінійного програмування

Неможливо розібрати вираз (невідома помилка): min F = x_{1}-x_{2}+2x_{3}-x_{4}-3x_{5}+x_{6}-2x_{7}

Розв’язання. Маємо n = 7 — кількість змінних, m = 5 — кількість обмежень. Виберемо як вільні змінні х1 та х2 і виразимо через них всі інші базисні змінні. З першого рівняння маємо:

Неможливо розібрати вираз (невідома помилка): x_{3}=-x_{1}+x_{2}+4

    (2.19.2)

З третього рівняння:

Неможливо розібрати вираз (невідома помилка): x_{5}=x_{1}+x_{2}+4

    (2.19.3)

а з четвертого:

Неможливо розібрати вираз (невідома помилка): x_{6}=-x_{2}+5

    (2.19.4)

Підставляючи (2.19.2) в друге рівняння системи і (2.19.4) в останнє, розв’язуємо їх відносно х4 та х7. Отримаємо:

Неможливо розібрати вираз (невідома помилка): x_{4}={3x}_{1}-{2x}_{2}+1;

Неможливо розібрати вираз (невідома помилка): x_{7}=-x_{1}+\frac{1}{2}x_{2}+6

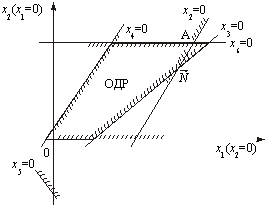
Далі за алгоритмом беремо х1 = 0 та х2 = 0 — координатні осі; інші обмежуючі прямі знаходимо, узявши х3 = 0, х4 = 0, х5 = 0, х6 = 0, х7 = 0. Багатокутник допустимих розв’язків зображено на рис. 2.12.

Література

Наконечний С. І., Савіна С. С. Математичне програмування: Навч. посіб. - К.: КНЕУ, 2003. - 452 с.