Графічний метод для задач ЛП N-вимірного простору при N більше 3

Розв'язувати графічним методом можна також задачі лінійного програмування n-вимірного простору, де n>3 , якщо при зведенні системи нерівностей задачі до системи рівнянь шляхом введення додаткових змінних кількість змінних n на дві більша, ніж число обмежень m, тобто n-m=2.

Тоді, як відомо з курсу вищої математики, можна дві з n змінних, наприклад Неможливо розібрати вираз (невідома помилка): X_1

та Неможливо розібрати вираз (невідома помилка):  X_2 

, вибрати як вільні, а інші m зробити базисними і виразити через вільні. Припустимо, що це зроблено. Отримаємо n-m=2 рівнянь вигляду:

Неможливо розібрати вираз (невідома помилка): \left\{ {\begin{array}{l} x_{3}=a_{31}x_{1}+a_{32}x_{2}+\beta_{1} \\ x_{4}=a_{41}x_{1}+a_{42}x_{2}+\beta_{2} \\ ................................ \\ x_{n}=a_{n1}x_{1}+a_{n2}x_{2}+\beta_{n} \\ \end{array}} \right.

Оскільки всі значення Неможливо розібрати вираз (невідома помилка): x_{i} \ge 0\;\,\,\,(i=\overline {1,n} )

то мають виконуватись умови:

Неможливо розібрати вираз (невідома помилка): x_{1}\ge 0,x_{2}\ge 0,

Неможливо розібрати вираз (невідома помилка): \left\{ {\begin{array}{l} x_{3}=a_{31}x_{1}+a_{32}x_{2}+\beta_{3}\ge 0 \\ x_{4}=a_{41}x_{1}+a_{42}x_{2}+\beta_{4}\ge 0 \\ ................................ \\ x_{n}=a_{n1}x_{1}+a_{n2}x_{2}+\beta_{n}\ge 0 \\ \end{array}}(1) \right.

Розглянемо, як можна зобразити ці умови геометрично. Візьмемо, наприклад, першу з них:

Неможливо розібрати вираз (невідома помилка): x_{3}=a_{31}x_{1}+a_{32}x_{2}+\beta_{3}\ge 0

Узявши величину Неможливо розібрати вираз (невідома помилка): x_{3}

рівною своєму крайньому значенню — нулю, отримаємо рівняння: Неможливо розібрати вираз (невідома помилка): a_{31}x_{1}+a_{32}x_{2}+\beta_{3}=0.

Це рівняння прямої. Для такої прямої Неможливо розібрати вираз (невідома помилка): x_{3}=0

, по одну сторону від неї Неможливо розібрати вираз (невідома помилка): x_{3}>0
, а по другу — Неможливо розібрати вираз (невідома помилка): x_{3}<0

. Відмітимо ту сторону прямої Неможливо розібрати вираз (невідома помилка): a_{31}x_{1}+a_{32}x_{2}+\beta_{3}=0

, де Неможливо розібрати вираз (невідома помилка): x_{3}<0

. В аналогічний спосіб побудуємо і всі інші обмежуючі прямі: Неможливо розібрати вираз (невідома помилка): x_{4}=0; x_{5}=0 ... x_{n}=0

і відмітимо для кожної з них півплощину, де відповідна змінна більше нуля.

У такий спосіб отримують n – 2 прямі та дві осі координат Неможливо розібрати вираз (невідома помилка): (x_{1}=0, x_{2}=0) . Кожна з них визначає півплощину, де виконується умова Неможливо розібрати вираз (невідома помилка): x_{i}>0\, (i=\overline {1,n-2} ) . Частина площини в Неможливо розібрати вираз (невідома помилка): x_{1}Ox_{2}

належить водночас всім півплощинам, утворюючи багатокутник допустимих розв’язків.

Припустимо, що в задачі необхідно знайти максимальне значення функціонала:

Неможливо розібрати вираз (невідома помилка): F=c_{1}x_{1}+c_{2}x_{2}+\, ..\, .+c_{n}x_{n}

Підставивши вирази для Неможливо розібрати вираз (невідома помилка): x_{3},\, x_{4}, \, x_{5} ... \, x_{n}

з (1) у цей функціонал, зведемо подібні доданки і отримаємо вираз лінійної функції F всіх n змінних лише через дві вільні змінні Неможливо розібрати вираз (невідома помилка):  X_1 
та Неможливо розібрати вираз (невідома помилка):  X_2 

Неможливо розібрати вираз (невідома помилка): F=y_{0}+y_{1}x_{1}+y_{2}x_{2}

, де Неможливо розібрати вираз (невідома помилка): Y_0

— вільний член, якого в початковому вигляді функціонала не було. Очевидно, що лінійна функція  Неможливо розібрати вираз (невідома помилка): F^{'}=y_{1}x_{1}+y_{2}x_{2}\, \, \,
досягає свого максимального значення за тих самих значень Неможливо розібрати вираз (невідома помилка):  X_1 
та Неможливо розібрати вираз (невідома помилка):  X_2 
, що й  Неможливо розібрати вираз (невідома помилка): F=y_{0}+y_{1}x_{1}+y_{2}x_{2}

. Отже, процедура відшукання оптимального плану з множини допустимих далі здійснюється за алгоритмом для випадку двох змінних.

Алгоритм графічного методу

Розглянемо задачу.

Знайти

max(min)Неможливо розібрати вираз (невідома помилка): Z=c_{1}x_{1}+c_{2}x_{2}

  (1.1)

Неможливо розібрати вираз (невідома помилка): \left\{ {\begin{array}{l} a_{11}x_{1}+a_{12}x_{2\left\{ \le ,=,\left. \ge \right\} \right.}b_{1}; \\ a_{21}x_{1}+a_{22}x_{2\left\{ \le ,=,\left. \ge \right\} \right.}b_{2}; \\ a_{31}x_{1}+a_{32}x_{2\left\{ \le ,=,\left. \ge \right\} \right.}b_{3}; \\ ................................ \\ a_{m1}x_{1}+a_{m2}x_{2\left\{ \le ,=,\left. \ge \right\} \right.}b_{m}; \\ \end{array}} \right. (1.2)

Неможливо розібрати вираз (невідома помилка): \left\{ {\begin{array}{l} x_{1}\ge 0,\, x_{2}\ge 0 \end{array}} \right. (1.3)

Припустимо, що система (1.2) за умов (1.3) сумісна і багатокутник її розв’язків обмежений.

Алгоритм графічного методу розв’язування задачі лінійного програмування складається з таких кроків:

1. Будуємо прямі, рівняння яких дістаємо заміною в обмеженнях задачі (1.2) знаків нерівностей на знаки рівностей.

2. Визначаємо півплощини, що відповідають кожному обмеженню задачі.

3. Знаходимо багатокутник розв’язків задачі лінійного програмування.

4. Будуємо вектор Неможливо розібрати вираз (невідома помилка): \overline N =(c_{1};c_{2})

, що задає напрям зростання значення цільової функції задачі.

5. Будуємо пряму Неможливо розібрати вираз (невідома помилка): c_{1}x_{1}+c_{2}x_{2}

= const, перпендикулярну до вектора Неможливо розібрати вираз (невідома помилка): \overline N 

.

6. Рухаючи пряму Неможливо розібрати вираз (невідома помилка): c_{1}x_{1}+c_{2}x_{2}

= const в напрямку вектора Неможливо розібрати вираз (невідома помилка): \overline N 
(для задачі максимізації) або в протилежному напрямі 

(для задачі мінімізації), знаходимо вершину багатокутника розв’язків, де цільова функція набирає екстремального значення.

7. Визначаємо координати точки, в якій цільова функція набирає максимального (мінімального) значення, і обчислюємо екстремальне значення цільової функції в цій точці.

У разі застосування графічного методу для розв’язування задач лінійного програмування можливі такі випадки:

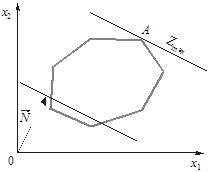
1. Цільова функція набирає максимального значення в єдиній вершині А багатокутника розв’язків (рис. 1.1)

Рис. 1.1

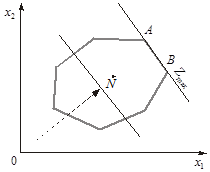
2. Максимального значення цільова функція досягає в будь-якій точці відрізка АВ (рис. 1.2). Тоді задача лінійного програмування має альтернативні оптимальні плани.

Рис. 1.2

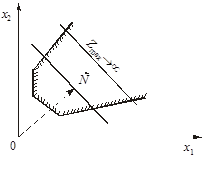
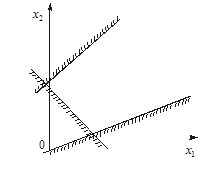
3. Задача лінійного програмування не має оптимальних планів: якщо цільова функція необмежена згори (рис. 1.3) або система обмежень задачі несумісна (рис. 1.4).

Рис. 1.3

Рис. 1.4

Приклад

Розв’язати графічним методом задачу лінійного програмування

Неможливо розібрати вираз (невідома помилка): min F = x_{1}-x_{2}+2x_{3}-x_{4}-3x_{5}+x_{6}-2x_{7}

Неможливо розібрати вираз (невідома помилка): \left\{ {\begin{array}{l} x_{1}-x_{2}+x_{3}=4; \\ 2x_{1}-x_{2}-x_{3}-x_{4}=-5; \\ x_{1}+x_{2}-x_{5}=-4; \\ x_{2}+x_{6}=5; \\ {2x}_{1}-{2x}_{2}-x_{6}+{2x}_{7}=7 \\ \end{array}} \right.

Неможливо розібрати вираз (невідома помилка): x_{i}\ge 0\, (i=\overline {1,7} )

Розв’язання. Маємо n = 7 — кількість змінних, m = 5 — кількість обмежень. Виберемо як вільні змінні х1 та х2 і виразимо через них всі інші базисні змінні. З першого рівняння маємо:

Неможливо розібрати вираз (невідома помилка): x_{3}=-x_{1}+x_{2}+4

    (1)

З третього рівняння:

Неможливо розібрати вираз (невідома помилка): x_{5}=x_{1}+x_{2}+4

    (2)

а з четвертого:

Неможливо розібрати вираз (невідома помилка): x_{6}=-x_{2}+5

    (3)

Підставляючи (1) в друге рівняння системи і (3) в останнє, розв’язуємо їх відносно х4 та х7. Отримаємо:

Неможливо розібрати вираз (невідома помилка): x_{4}={3x}_{1}-{2x}_{2}+1;

Неможливо розібрати вираз (невідома помилка): x_{7}=-x_{1}+\frac{1}{2}x_{2}+6

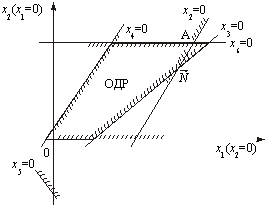
Далі за алгоритмом беремо х1 = 0 та х2 = 0 — координатні осі; інші обмежуючі прямі знаходимо, узявши х3 = 0, х4 = 0, х5 = 0, х6 = 0, х7 = 0. Багатокутник допустимих розв’язків зображено на рис. 1

Рис. 1

Знайдемо вигляд функціонала, вираженого через х1 та х2. Для цього знайдені щойно вирази для х3, х4, х5, х6 та х7 через вільні змінні х1 і х2 підставимо у функціонал і, звівши подібні члени, отримаємо:

Неможливо розібрати вираз (невідома помилка): F=-{5x}_{1}-{2x}_{2}-12

Відкидаючи вільний член, маємо: Неможливо розібрати вираз (невідома помилка): F=-{5x}_{1}-{2x}_{2}

Будуємо вектор Неможливо розібрати вираз (невідома помилка): N (-5,-2) , перпендикулярно до нього — пряму Неможливо розібрати вираз (невідома помилка): F^{'} . Рухаючи пряму Неможливо розібрати вираз (невідома помилка): F^{'}

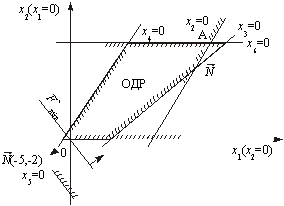
в напрямку, протилежному N (необхідно знайти мінімальне значення функції F), отримаємо точку мінімуму — А (рис. 2).

Рис. 2

У точці А перетинаються дві обмежуючі прямі: х6 = 0 та х7 = 0. Отже, для відшукання її координат необхідно розв’язати систему рівнянь:

Неможливо розібрати вираз (невідома помилка): \left\{ {\begin{array}{l} {-x}_{2}+5=0 \\ {-x}_{1}-\frac{1}{2}x_{2}+6=0 \\ \end{array}} \right.

Розв’язком системи є Неможливо розібрати вираз (невідома помилка): x_{1}^{'}=8,5; x_{2}^{'}=5 . Підставивши ці значення у відповідні вирази, знайдемо оптимальні значення базисних змінних: Неможливо розібрати вираз (невідома помилка): x_{3}^{'}=0,5;\, x_{4}^{'}=16,5;\, x_{5}^{'}=17,5;\, x_{6}^{'}=0;\, x_{7}^{'}=0

Підстановкою значень Неможливо розібрати вираз (невідома помилка): x_{1}^{'}

та Неможливо розібрати вираз (невідома помилка): x_{2}^{'}
в лінійну функцію F отримуємо значення цільової функції:

Неможливо розібрати вираз (невідома помилка): F^{'}=-5\times 8,5-2\times 5-12=-64,5

Література

Наконечний С. І., Савіна С. С. Математичне програмування: Навч. посіб. - К.: КНЕУ, 2003. - 452 с.