Відмінності між версіями «Невизначені інтеграли»
Матеріал з Вікі ЦДУ
Lilit (обговорення • внесок) |
Lilit (обговорення • внесок) |
||
| Рядок 1: | Рядок 1: | ||
| − | <p align=center>'''Невизначений інтеграл'''</p> | + | == <p align=center>'''Невизначений інтеграл'''</p> == |
| + | |||
Неви́значений інтегра́л для функції '''f''' — це сукупність усіх [[первісних]] цієї функції. | Неви́значений інтегра́л для функції '''f''' — це сукупність усіх [[первісних]] цієї функції. | ||
| Рядок 12: | Рядок 13: | ||
##[[Метод інтегрування частинами.]] | ##[[Метод інтегрування частинами.]] | ||
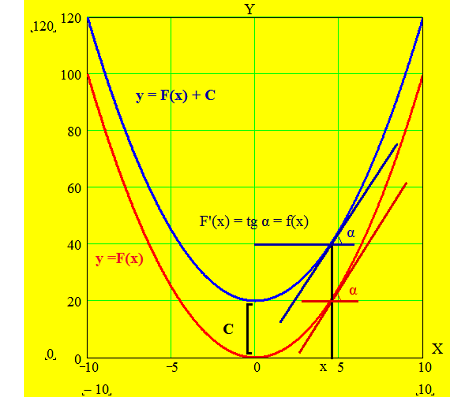
<p align=center>[[Файл:невизнінтеграл.png]]</p> | <p align=center>[[Файл:невизнінтеграл.png]]</p> | ||
| + | == '''[[Програма Maple і застосування її до знаходження невизначеного інтегралу]]'''== | ||
| + | <p align=center>[[Файл:803.jpeg]]</p> | ||
Поточна версія на 17:24, 22 травня 2014
Невизначений інтеграл
Неви́значений інтегра́л для функції f — це сукупність усіх первісних цієї функції. Задача диференціального числення — знаходження похідної від заданої функції y = f(x). Задача інтегрального числення протилежна: потрібно визначити функцію, похідна від якої відома. Фундаментальними поняттями інтегрального числення є поняття первісної та невизначеного інтегралу.
Зміст
- Невизначений інтеграл;
- Властивості невизначеного інтеграла;
- Методи обчислення невизначених інтегралів:
Програма Maple і застосування її до знаходження невизначеного інтегралу
