Відмінності між версіями «Однорідні лінійне диференціальні рівняння»
Матеріал з Вікі ЦДУ
Lilit (обговорення • внесок) (Створена сторінка: <p align=center>'''Диференціальні рівняння'''</p> :Диференціальні рівняння — розділ математики, як...) |
Lilit (обговорення • внесок) |
||
| Рядок 1: | Рядок 1: | ||
<p align=center>'''Диференціальні рівняння'''</p> | <p align=center>'''Диференціальні рівняння'''</p> | ||
| − | :Диференціальні рівняння — розділ математики, який вивчає теорію та способи розв'язування рівнянь, що містять шукану функцію та її похідні різних порядків одного аргументу (звичайні диференціальні) чи кількох аргументів (диференціальні рівняння в частинних похідних). Диференціальні рівняння широко використовуються на практиці, зокрема для опису перехідних процесів. | + | :''Диференціальні рівняння''— розділ математики, який вивчає теорію та способи розв'язування рівнянь, що містять шукану функцію та її похідні різних порядків одного аргументу (звичайні диференціальні) чи кількох аргументів (диференціальні рівняння в частинних похідних).Диференціальні рівняння широко використовуються на практиці, зокрема для опису перехідних процесів. |
Лінійне диференціальне рівняння — звичайне диференціальне рівняння, в яке невідома функція та її похідні входять лінійно, тобто рівняння вигляду: | Лінійне диференціальне рівняння — звичайне диференціальне рівняння, в яке невідома функція та її похідні входять лінійно, тобто рівняння вигляду: | ||
<p align=center>[[Файл:760.png]]</p> | <p align=center>[[Файл:760.png]]</p> | ||
Версія за 23:15, 21 травня 2014
Диференціальні рівняння
- Диференціальні рівняння— розділ математики, який вивчає теорію та способи розв'язування рівнянь, що містять шукану функцію та її похідні різних порядків одного аргументу (звичайні диференціальні) чи кількох аргументів (диференціальні рівняння в частинних похідних).Диференціальні рівняння широко використовуються на практиці, зокрема для опису перехідних процесів.
Лінійне диференціальне рівняння — звичайне диференціальне рівняння, в яке невідома функція та її похідні входять лінійно, тобто рівняння вигляду:
- Важливий підклас лінійних диференційних рівнянь складають лінійні диференційні рівняння зі сталими коефіцієнтами, для яких
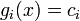 .
.
Рівняння
називається однорідним лінійним диференційним рівнянням.
