Модифіковані функції Беселя
Модифіковані функції Бесселя - це функції Бесселя від уявного аргументу. Якщо в диференціальному рівнянні Бесселя
- Неможливо розібрати вираз (невідома помилка): z^2 \frac{d^2 \omega}{dz^2} + z \frac{d\omega}{dz} + (z^2 - \nu^2)\omega = 0
замінити Неможливо розібрати вираз (невідома помилка): \ z
на Неможливо розібрати вираз (невідома помилка): \ iz
, воно набуде вигляду
- Неможливо розібрати вираз (невідома помилка): z^2 \frac{d^2 \omega}{dz^2} + z \frac{d\omega}{dz} - (z^2 + \nu^2)\omega = 0, \qquad (1)
Це рівняння називається модифікованим рівнянням Бесселя. Якщо Неможливо розібрати вираз (невідома помилка): ~\nu
не є цілим числом, то функції Бесселя Неможливо розібрати вираз (невідома помилка): ~J_\nu(iz)
и Неможливо розібрати вираз (невідома помилка): ~J_{-\nu}(iz)
є двома лінійно незалежними розв'язками рівняння Неможливо розібрати вираз (невідома помилка): ~(1)
, проте частіше використовують функції
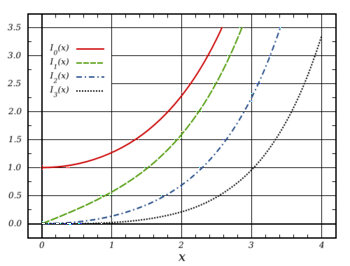
- Неможливо розібрати вираз (невідома помилка): I_\nu(z)=e^{-\frac{i\nu\pi}{2}}J_ \nu \left( z e^{\frac{i\pi}{2}}\right)=\sum^\infty_{k=0}\frac{\left( \dfrac{z}{2} \right)^{2k+\nu}}{k!\Gamma(k+\nu+1)}
и Неможливо розібрати вираз (невідома помилка): ~I_{-\nu}(z).
Їх називають модифікованими функціями Бесселя першого роду або функціями Інфельда.
Якщо Неможливо розібрати вираз (невідома помилка): ~\nu
- дійсне число, а Неможливо розібрати вираз (невідома помилка): ~z - додатнє, ці функції приймають дійсні значення.
Неможливо розібрати вираз (невідома помилка): ~\nu
називається порядком функції.
Функція
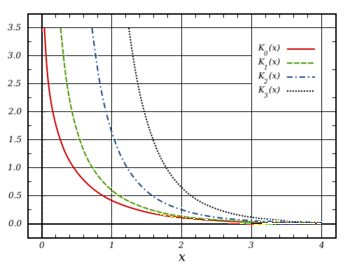
- Неможливо розібрати вираз (невідома помилка): ~K_\nu(z)=\frac{\pi}{2\sin \nu\pi}\biggl[I_\nu(z)-I_{-\nu}(z)\biggr]
також є розв'язком рівняння Неможливо розібрати вираз (невідома помилка): ~(1) . Її називають модифікованою функцією Бесселя другого роду або функцією Макдональда. очевидно, що
- Неможливо розібрати вираз (невідома помилка): ~K_\nu(z)=K_{-\nu}(z)
і приймає дійсні значення, якщо Неможливо розібрати вираз (невідома помилка): ~\nu
— дійсне число, а Неможливо розібрати вираз (невідома помилка): ~z — додатнє.
Зміст
Рекурентні співвідношення та формули диференціювання
Модифіковані функції Бесселя першого роду
- Неможливо розібрати вираз (невідома помилка): ~\left(\frac{d}{zdz}\right)^m\Bigl[z^\nu I_\nu(z) \Bigr]=z^{\nu-m} I_{\nu-m}(z).
- Неможливо розібрати вираз (невідома помилка): ~\left(\frac{d}{zdz}\right)^m\Bigl[z^{-\nu} I_\nu(z) \Bigr]=z^{-\nu-m} I_{\nu+m}(z).
- Неможливо розібрати вираз (невідома помилка): ~I_{\nu-1}(z)-I_{\nu+1}(z)=2\nu z^{-1} I_\nu(z).
- Неможливо розібрати вираз (невідома помилка): ~I_{\nu-1}(z)+I_{\nu+1}(z)=2I'_\nu(z).
Модифіковані функції Бесселя другого роду
- Неможливо розібрати вираз (невідома помилка): ~\left(\frac{d}{zdz}\right)^m\Bigl[z^\nu K_\nu(z) \Bigr]=(-1)^m z^{\nu-m} K_{\nu-m}(z).
- Неможливо розібрати вираз (невідома помилка): ~\left(\frac{d}{zdz}\right)^m\Bigl[z^{-\nu} K_\nu(z) \Bigr]=(-1)^m z^{-\nu-m} K_{\nu+m}(z).
- Неможливо розібрати вираз (невідома помилка): ~K_{\nu-1}(z)-K_{\nu+1}(z)=-2\nu z^{-1} K_\nu(z).
- Неможливо розібрати вираз (невідома помилка): ~K_{\nu-1}(z)+K_{\nu+1}(z)=-2K'_\nu(z).
Вронскіан системи модифікованих функцій Бесселя
- Неможливо розібрати вираз (невідома помилка): W\left[I_\nu(z),I_{-\nu}(z)\right]=-\frac{2\sin(\nu\pi)}{\pi z}.
- Неможливо розібрати вираз (невідома помилка): W\left[I_\nu(z),K_\nu (z)\right]=z^{-1}.
Інтегральні представлення
Модифіковані функції Бесселя першого роду
- Неможливо розібрати вираз (невідома помилка): I_\nu (z)=\frac{2^{-\nu}z^\nu}{\sqrt{\pi}\Gamma(\nu+\frac12)}\int_0^\pi e^{z\cos t}\left(\sin t\right)^{2\nu} dt, \qquad Re(\nu)>-\frac12, \Gamma(z)
— гамма-функція.
- Неможливо розібрати вираз (невідома помилка): I_\nu (z)=\frac{2^{1-\nu}z^\nu}{\sqrt{\pi}\Gamma(\nu+\frac12)}\int_0^1 (1-t^2)^{\nu-\frac12}\cosh(zt) dt, \qquad Re(\nu)>-\frac12.
- Неможливо розібрати вираз (невідома помилка): I_\nu (z)=\frac{2^{-\nu}z^\nu}{\sqrt{\pi}\Gamma(\nu+\frac12)}\int_{-1}^1 (1-t^2)^{\nu-\frac12} e^{-zt} dt, \qquad Re(\nu)>-\frac12.
- Неможливо розібрати вираз (невідома помилка): I_n(z)=\frac{1}{\pi}\int_0^\pi e^{z\cos t}\cos (nt)dt, \qquad n \in \mathbb Z, Re(z)>0.
Модифіковані функції Бесселя другого роду
- Неможливо розібрати вираз (невідома помилка): K_\nu(z)=\int_0^\infty e^{-z\cosh t}\cosh (\nu t)dt, \qquad Re(z)>0.
- Неможливо розібрати вираз (невідома помилка): K_\nu (z)=\frac{\sqrt{\pi}z^\nu}{\Gamma(\nu+\frac12)}\int_1^\infty (t^2-1)^{\nu-\frac12}e^{-zt} dt, \qquad Re(\nu)>-\frac12, Re(z)>0.
- Неможливо розібрати вираз (невідома помилка): K_\nu (z)=\frac{\sqrt{\pi}z^\nu}{\Gamma(\nu+\frac12)}\int_0^\infty e^{-z\cosh t}\left(\sinh t \right)^{2\nu} dt, \qquad Re(\nu)>-\frac12, Re(z)>0.
Асимптотична поведінка
- Неможливо розібрати вираз (невідома помилка): I_\nu(z)\varpropto \frac{e^z}{\sqrt{2\pi z}}\left(1+O\left(\frac{1}{z} \right) \right), \qquad \left|Arg(z)\right|<\frac{\pi}{2},\left|z\right| \to \infty.
- Неможливо розібрати вираз (невідома помилка): K_\nu(z)\varpropto \sqrt{\frac{\pi}{2}}\frac{e^{-z}}{\sqrt{z}}\left(1+O\left(\frac{1}{z} \right) \right), \qquad \left|z\right| \to \infty.
Виконала: Куян Юлія