Відмінності між версіями «Hgudsyfgduoiaybpiu»

Матеріал з Вікі ЦДУ
Перейти до: навігація, пошук
 
Рядок 1: Рядок 1:
−
<math>\frac{d^2\omega}{dz^2} + \frac{1-2a}{z}\frac{d\omega}{dz} + \Bigl[(bcz^{c-1})^2+\frac{a^2-m^2c^2}{z^2}\Bigr]\omega=0 </math>
+
'''Опції Бесселя''' в [http://ru.wikipedia.org/wiki/Математика математиці] - сім'я [http://ru.wikipedia.org/wiki/Функция_(математика) функцій], які є канонічними розв'язками [http://ru.wikipedia.org/wiki/Дифференциальное_уравнение диференціального рівняння Бесселя]:
 +
: <math>x^2 \frac{d^2 y}{dx^2} + x \frac{dy}{dx} + (x^2 - \alpha^2)y = 0,</math>
  
−
<math> \omega = z^aZ_m \left(bz^c \right)  </math>
+
де <math>\alpha</math> — довільне [http://ru.wikipedia.org/wiki/Действительное_число дійсне число], яке називається '''порядком'''.
  
−
<math>\frac{d^2\omega}{dz^2} + \frac{1}{z}\frac{d\omega}{dz} + \Bigl[1 - \frac{m^2}{z^2}\Bigr]\omega=0  </math>
+
Найбільш часто використовуються функції Бесселя цілих порядків.
  
 +
Хоча <math>\alpha</math> и <math>(-\alpha)</math> породжують однакові рівняння, зазвичай домовляються про те, щоб їм відповідали різні функції (це робиться, наприклад, для того, щоб функція Бесселя була гладкою по <math>\alpha</math> ).
  
−
<math> \omega = Z_m \left(z \right) (a=0,b=c=1)</math>
+
Функції Бесселя вперше були визначені [[Швейцарія | швейцарським]] математиком [http://ru.wikipedia.org/wiki/Бернулли,_Даниил Даніелем Бернуллі], а названі на честь [http://ru.wikipedia.org/wiki/Бессель,_Фридрих_Вильгельм Фрідріха Бесселя].
 +
 
 +
== Застосування ==
 +
Рівняння Бесселя виникає під час знаходження розв'язків [http://ru.wikipedia.org/wiki/Уравнение_Лапласа рівняння Лапласа] та [http://ru.wikipedia.org/wiki/Уравнение_Гельмгольца рівняння Гельмгольца] в [http://ru.wikipedia.org/wiki/Цилиндрические_координаты циліндричних] та [http://ru.wikipedia.org/wiki/Сферические_координаты сферичних] координатах. Тому функції Бесселя застосовуються при розв'язаніі багатьох задач про поширення хвиль, статичних потенціалах і т. п., наприклад:
 +
 
 +
* теплопровідність в циліндричних об'єктах;
 +
* Форми коливання тонкої круглої мембрани
 +
* Швидкість частинок в циліндрі, заповненому рідиною і який обертається навколо своєї осі.
 +
Функції Бесселя застосовуються і в рішенні інших задач, наприклад, при обробці сигналів.
 +
 
 +
== Визначення ==
 +
Оскільки наведене рівняння є рівнянням другого порядку, у нього має бути два [[лінійна залежність | лінійно незалежних]] рішення. Проте залежно від обставин вибираються різні визначення цих рішень. Нижче наведені деякі з них.
 +
 
 +
=== Функції Бесселя першого роду ===
 +
Функціями Бесселя першого роду, які позначаються <math>J_\alpha(x)</math>, є розв'язки, скінченні в точці <math>x=0</math> при цілих або невід'ємних <math>\alpha</math>. Вибір конкретної функції і її нормалізації визначаються її властивостями. Можна визначити ці функції за допомогою розкладу в [http://ru.wikipedia.org/wiki/Ряд_Тейлора ряд Тейлора] в околі нуля (або в більш загальний [[степеневий ряд]] при нецілих <math>\alpha</math>):
 +
: <math> J_\alpha(x) = \sum_{m=0}^\infty \frac{(-1)^m}{m!\, \Gamma(m+\alpha+1)} {\left({\frac{x}{2}}\right)}^{2m+\alpha} </math>
 +
Тут <math>\Gamma(z)</math> - Це [[гамма-функція Ейлера]], узагальнення [[факторіал]]а на нецілі значення. Графік функції Бесселя схожий на [[синус (функція) | синусоїду]], коливання якої затухають пропорційно <math>\frac{1}{\sqrt{x}}</math>, хоча насправді нулі функції розташовані не періодично.
 +
 
 +
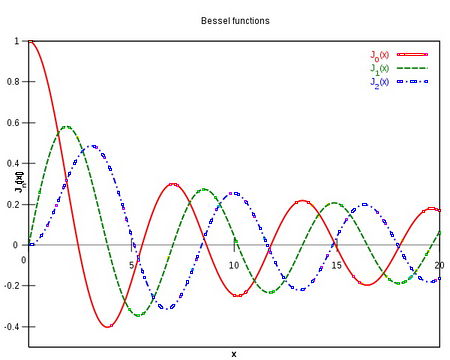
Нижче наведені графіки <math>J_\alpha (x)</math> для <math>\alpha = 0, 1, 2</math>:
 +
 +
[[Файл:600px-BesselJ_plot111.jpg|center|450px|График функции Бесселя первого рода J]]
 +
 
 +
Якщо <math>\alpha</math> не є цілим числом, функції <math>J_\alpha (x)</math> и <math>J_{-\alpha} (x)</math> лінійно незалежні і, отже, є рішеннями рівняння. Але якщо <math>\alpha</math> ціле, то вірно наступне співвідношення:
 +
 
 +
: <math>J_{-\alpha}(x) = (-1)^{\alpha} J_{\alpha}(x)\,</math>
 +
 
 +
Воно означає, що в цьому випадку функції лінійно залежні. Тоді другим рішенням рівняння стане функція Бесселя другого роду.
 +
 
 +
==== Інтеграли Бесселя ====
 +
Можна дати інше визначення функції Бесселя для цілих значень <math>\alpha</math>, використовуючи інтегральне представлення:
 +
 
 +
: <math>J_\alpha (x) = \frac{1}{\pi} \int\limits_{0}^{\pi}\!\cos (\alpha \tau - x \sin \tau)\,d\tau</math>
 +
 
 +
Цей підхід використовував Бесселя, вивчивши з його допомогою деякі властивості функцій. Можливо і інше інтегральне представлення:
 +
 
 +
: <math>J_\alpha (x) = \frac{1}{2 \pi} \int\limits_{-\pi}^{\pi}\!e^{i(\alpha \tau - x \sin \tau)}\,d\tau</math>

Поточна версія на 16:15, 20 травня 2010

Опції Бесселя в математиці - сім'я функцій, які є канонічними розв'язками диференціального рівняння Бесселя:

Неможливо розібрати вираз (невідома помилка): x^2 \frac{d^2 y}{dx^2} + x \frac{dy}{dx} + (x^2 - \alpha^2)y = 0,


де Неможливо розібрати вираз (невідома помилка): \alpha  — довільне дійсне число, яке називається порядком.

Найбільш часто використовуються функції Бесселя цілих порядків.

Хоча Неможливо розібрати вираз (невідома помилка): \alpha 

и Неможливо розібрати вираз (невідома помилка): (-\alpha)
породжують однакові рівняння, зазвичай домовляються про те, щоб їм відповідали різні функції (це робиться, наприклад, для того, щоб функція Бесселя була гладкою по Неможливо розібрати вираз (невідома помилка): \alpha
).

Функції Бесселя вперше були визначені швейцарським математиком Даніелем Бернуллі, а названі на честь Фрідріха Бесселя.

Застосування

Рівняння Бесселя виникає під час знаходження розв'язків рівняння Лапласа та рівняння Гельмгольца в циліндричних та сферичних координатах. Тому функції Бесселя застосовуються при розв'язаніі багатьох задач про поширення хвиль, статичних потенціалах і т. п., наприклад:

  • теплопровідність в циліндричних об'єктах;
  • Форми коливання тонкої круглої мембрани
  • Швидкість частинок в циліндрі, заповненому рідиною і який обертається навколо своєї осі.

Функції Бесселя застосовуються і в рішенні інших задач, наприклад, при обробці сигналів.

Визначення

Оскільки наведене рівняння є рівнянням другого порядку, у нього має бути два лінійно незалежних рішення. Проте залежно від обставин вибираються різні визначення цих рішень. Нижче наведені деякі з них.

Функції Бесселя першого роду

Функціями Бесселя першого роду, які позначаються Неможливо розібрати вираз (невідома помилка): J_\alpha(x) , є розв'язки, скінченні в точці Неможливо розібрати вираз (невідома помилка): x=0 

при цілих або невід'ємних Неможливо розібрати вираз (невідома помилка): \alpha

. Вибір конкретної функції і її нормалізації визначаються її властивостями. Можна визначити ці функції за допомогою розкладу в ряд Тейлора в околі нуля (або в більш загальний степеневий ряд при нецілих Неможливо розібрати вираз (невідома помилка): \alpha ):

Неможливо розібрати вираз (невідома помилка): J_\alpha(x) = \sum_{m=0}^\infty \frac{(-1)^m}{m!\, \Gamma(m+\alpha+1)} {\left({\frac{x}{2}}\right)}^{2m+\alpha}

Тут Неможливо розібрати вираз (невідома помилка): \Gamma(z) 

- Це гамма-функція Ейлера, узагальнення факторіала на нецілі значення. Графік функції Бесселя схожий на  синусоїду, коливання якої затухають пропорційно Неможливо розібрати вираз (невідома помилка): \frac{1}{\sqrt{x}}

, хоча насправді нулі функції розташовані не періодично.

Нижче наведені графіки Неможливо розібрати вираз (невідома помилка): J_\alpha (x) 

для Неможливо розібрати вираз (невідома помилка): \alpha = 0, 1, 2
График функции Бесселя первого рода J

Якщо Неможливо розібрати вираз (невідома помилка): \alpha 

не є цілим числом, функції Неможливо розібрати вираз (невідома помилка): J_\alpha (x)
и Неможливо розібрати вираз (невідома помилка): J_{-\alpha} (x)
лінійно незалежні і, отже, є рішеннями рівняння. Але якщо Неможливо розібрати вираз (невідома помилка): \alpha
ціле, то вірно наступне співвідношення:
Неможливо розібрати вираз (невідома помилка): J_{-\alpha}(x) = (-1)^{\alpha} J_{\alpha}(x)\,


Воно означає, що в цьому випадку функції лінійно залежні. Тоді другим рішенням рівняння стане функція Бесселя другого роду.

Інтеграли Бесселя

Можна дати інше визначення функції Бесселя для цілих значень Неможливо розібрати вираз (невідома помилка): \alpha , використовуючи інтегральне представлення:

Неможливо розібрати вираз (невідома помилка): J_\alpha (x) = \frac{1}{\pi} \int\limits_{0}^{\pi}\!\cos (\alpha \tau - x \sin \tau)\,d\tau


Цей підхід використовував Бесселя, вивчивши з його допомогою деякі властивості функцій. Можливо і інше інтегральне представлення:

Неможливо розібрати вираз (невідома помилка): J_\alpha (x) = \frac{1}{2 \pi} \int\limits_{-\pi}^{\pi}\!e^{i(\alpha \tau - x \sin \tau)}\,d\tau
Отримано з https://wiki.cusu.edu.ua/index.php?title=Hgudsyfgduoiaybpiu&oldid=29094