Економічна інтерпретація прямої та двоїстої задач ЛП. Правила побудови двоїстих задач
Економічна інтерпретація прямої та двоїстої задач ЛП
Кожна задача лінійного програмування пов’язана з іншою, так званою двоїстою задачею.
Пряма задача: Неможливо розібрати вираз (невідома помилка): max F = c_1x_1 + c_2x_2 + … + c_nx_n
(1)
Неможливо розібрати вираз (невідома помилка): \left\{ {\begin{array}{l} a_{11}x_{1}+a_{12}x_{2}+...+a_{1n}x_{n} \le b_1 \\ a_{21}x_{1}+a_{22}x_{2}+...+a_{2n}x_{n} \le b_2 \\ ................................ \\ a_{m1}x_{1}+a_{m2}x_{2}+...+a_{mn}x_{n} \le b_m \\ \end{array}} \right.
(2)
Неможливо розібрати вираз (невідома помилка): x_j \ge 0 , j= \overline{1,n}
(3)
Необхідно визначити, яку кількість продукції кожного j-го виду Неможливо розібрати вираз (невідома помилка): x_j ( j= \overline{1,n} )
необхідно виготовляти в процесі виробництва, щоб максимізувати загальну виручку від реалізації продукції під-приємства. Причому відомі: наявні обсяги ресурсів — Неможливо розібрати вираз (невідома помилка): b_i ( i= \overline{1,m} )
; норми витрат і-го виду ресурсу на виробництво одиниці j-го виду продукції — Неможливо розібрати вираз (невідома помилка): a_{ij} ( i= \overline{1,m}, j= \overline{1,n} )
, а також Неможливо розібрати вираз (невідома помилка): c_j ( j= \overline{1,n} )
— ціни реалізації одиниці j-ої продукції.
Нехай доцільно продавати деяку частину чи всі наявні ресурси.
Позначимо Неможливо розібрати вираз (невідома помилка): y_i
— ціна одиниці і-го ресурсу.
Необхідно визначити такі ціни ресурсів щоб загальна ціна на них була мінімально. Продавати ресурси доцільно лише за умо-ви, що виручка, отримана від продажу ресурсів, перевищує суму, яку можна було б отримати від реалізації продукції, виготовленої з тих самих обсягів ресурсів, тобто: Неможливо розібрати вираз (невідома помилка): min Z = b_1y_1 + b_2y_2 + … + b_ny_n
(4)
за умов:
Неможливо розібрати вираз (невідома помилка): \left\{ {\begin{array}{l} a_{11}y_{1}+a_{12}y_{2}+...+a_{1n}y_{n} \ge c_1 \\ a_{21}y_{1}+a_{22}y_{2}+...+a_{2n}y_{n} \ge c_2 \\ ................................ \\ a_{m1}y_{1}+a_{m2}y_{2}+...+a_{mn}y_{n} \ge c_m \\ \end{array}} \right.
(5)
Неможливо розібрати вираз (невідома помилка): y_i \ge 0 , i= \overline{1,m}
(6)
Необхідно визначити, які мінімальні ціни можна встановити для одиниці кожного і-го виду ресурсу Неможливо розібрати вираз (невідома помилка): y_i, i= \overline{1,m}
щоб продаж ресурсів був доцільнішим, ніж виробництво продукції.
Зауважимо, що справжній зміст величин Неможливо розібрати вираз (невідома помилка): y_i, i= \overline{1,m}
— умовні ціни, що виражають рівень «цінності» відповідного ресурсу для даного виробництва. Англійський термін «shadow prices» у літе-ратурі перекладають як «оцінка» або «тіньова, неявна ціна». Ака-демік Л. В. Канторович назвав їх об’єктивно обумовленими оці-н¬ками відповідного ресурсу.
Початкова постановка задачі та математична модель може мати вигляд як (1)—(3), так і (4)—(6). Отже, як правило, кажуть про пару спряжених задач лінійного програмування.
Правила побудови двоїстих задач
Вважають, що задача лінійного програмування подана у стан-дартному вигляді, якщо в задачі максимізації всі обмежень при-ведені до виду « Неможливо розібрати вираз (невідома помилка): \le
», а для задачі мінімізації — до виду « Неможливо розібрати вираз (невідома помилка): \ge ».
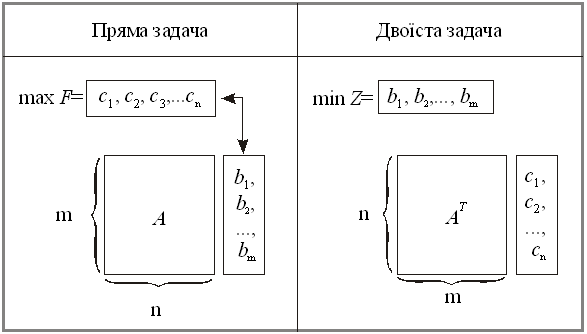
Якщо пряма задача лінійного програмування подана в стандарт¬ному вигляді, то двоїста задача утворюється прави-лами: 1. Кожному обмеженню прямої задачі відповідає змінна двоїс-тої задачі. Кількість невідомих двоїстої задачі дорівнює кількості обмежень прямої задачі. 2. Кожній змінній прямої задачі відповідає обмеження двоїстої задачі, причому кількість обмежень двоїстої задачі дорівнює кількості невідомих прямої задачі. 3. Якщо цільова функція прямої задачі задається на пошук найбільшого значення (max), то цільова функція двоїстої задачі — на визначення найменшого значення (min), і навпаки. 4. Коефіцієнтами при змінних у цільовій функції двоїстої за-дачі є вільні члени системи обмежень прямої задачі. 5. Правими частинами системи обмежень двоїстої задачі є ко-ефіцієнти при змінних у цільовій функції прямої задачі. 6. Матриця коефіцієнтів при змінних у системі обмежень прямої задачі, і матриця коефіцієнтів у системі обмежень двої-стої задачі утворюються одна з одної транспонуванням
Схема побудови двоїстої задачі до прямої
У симетричних задачах обмеження прямої та двоїстої задач є лише нерівностями, а змінні обох задач можуть набувати лише невід’ємних значень.
У несиметричних задачах деякі обмеження прямої задачі можуть бути рівняннями, а двоїстої — лише нерівностями. У цьому разі відповідні рівнянням змінні двоїстої задачі можуть набувати будь-яких значень, не обмежених знаком.
| Пряма задача | Двоїста задача |
| Cиметричні задачі | |
| Неможливо розібрати вираз (невідома помилка): max F = CX | Неможливо розібрати вираз (невідома помилка): min Z = BY |
| Неможливо розібрати вираз (невідома помилка): AX \le B | Неможливо розібрати вираз (невідома помилка): A^TY \ge C |
| Неможливо розібрати вираз (невідома помилка): X \ge 0 | Неможливо розібрати вираз (невідома помилка): Y \ge 0 |
| Неможливо розібрати вираз (невідома помилка): max F = CX | Неможливо розібрати вираз (невідома помилка): nax Z = BY |
| Неможливо розібрати вираз (невідома помилка): AX \ge B | Неможливо розібрати вираз (невідома помилка): A^TY \le C |
| Неможливо розібрати вираз (невідома помилка): X \ge 0 | Неможливо розібрати вираз (невідома помилка): Y \ge 0 |
| Несиметричні задачі | |
| Неможливо розібрати вираз (невідома помилка): max F = CF | Неможливо розібрати вираз (невідома помилка): min Z = BY |
| Неможливо розібрати вираз (невідома помилка): AX = B | Неможливо розібрати вираз (невідома помилка): A^TY \ge C |
| Неможливо розібрати вираз (невідома помилка): X \le 0 | Неможливо розібрати вираз (невідома помилка): Y \in [-\propto ; \propto ] |
| Неможливо розібрати вираз (невідома помилка): min F = CX | Неможливо розібрати вираз (невідома помилка): max Z = BY |
| Неможливо розібрати вираз (невідома помилка): AX = B | Неможливо розібрати вираз (невідома помилка): A^TY \le C |
| Неможливо розібрати вираз (невідома помилка): X \ge | Неможливо розібрати вираз (невідома помилка): Y \in [-\propto ; \propto ] |