Відмінності між версіями «Інтеграли Френеля та інтеграл ймовірностей»
| Рядок 1: | Рядок 1: | ||
[[Файл:250px-Fresnel Integrals (Unnormalised).svg.png|250px|thumb| | [[Файл:250px-Fresnel Integrals (Unnormalised).svg.png|250px|thumb| | ||
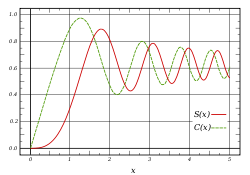
| − | <font color=#b30000>''S''(''x'')</font> и <font color=#00b300>''C''(''x'')</font>. | + | <font color=#b30000>''S''(''x'')</font> и <font color=#00b300>''C''(''x'')</font>.Максимальне значення для''C''(''x'') приблизно дорівнює 0.977451424. Якщо використовувати <math>\pi t^2</math> замість <math>t^2</math>, то графік змінить вертикальний и горизонтальний масштаб (см. ниже).]] |
| − | ''' | + | '''Інтеграли Френеля''' ''S''(''x'') и ''C''(''x'') — це [[спеціальні функції]], названі на честь [[Френель, Огюстен Жан|Огюстена Жана Френеля]] і використовуються в [[Оптиці|оптиці]]. Вони виникають при розрахунку [[Дифракція Френеля|дифракції Френеля]] і визначаються як |
: <math>S(x)=\int\limits_0^x \sin(t^2)\,dt,\quad C(x)=\int\limits_0^x \cos(t^2)\,dt.</math> | : <math>S(x)=\int\limits_0^x \sin(t^2)\,dt,\quad C(x)=\int\limits_0^x \cos(t^2)\,dt.</math> | ||
| − | + | Параметричний графік ''S''(''x'') и ''C''(''x'') дає криву на площині, яка має назву '''спіраль Корню''' | |
| − | == | + | == Розклад в ряд == |
| − | [[Файл:Fresnel Integrals (Normalised).svg|250px|thumb | + | [[Файл:250px-Fresnel Integrals (Normalised).svg.png|250px|thumb]] |
| − | + | ||
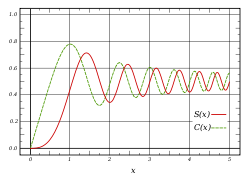
| − | + | Інтеграли Френеля можуть бути представлені [[Ряд Тейлора|степеневими рядами]], збіжними при всіх ''x'': | |
: <math>S(x)=\int\limits_0^x \sin(t^2)\,dt=\sum_{n=0}^{\infin}(-1)^n\frac{x^{4n+3}}{(4n+3)(2n+1)!},</math> | : <math>S(x)=\int\limits_0^x \sin(t^2)\,dt=\sum_{n=0}^{\infin}(-1)^n\frac{x^{4n+3}}{(4n+3)(2n+1)!},</math> | ||
: <math>C(x)=\int\limits_0^x \cos(t^2)\,dt=\sum_{n=0}^{\infin}(-1)^n\frac{x^{4n+1}}{(4n+1)(2n)!}.</math> | : <math>C(x)=\int\limits_0^x \cos(t^2)\,dt=\sum_{n=0}^{\infin}(-1)^n\frac{x^{4n+1}}{(4n+1)(2n)!}.</math> | ||
| − | + | Рівняння 7.3.1 — 7.3.2</ref> використовують в якості аргумента тригонометричних підінтегральних функцій <math>\frac{\pi}{2}t^2</math>. | |
| − | == | + | == Спіраль Корню == |
[[Файл:480px-Cornu Spiral.svg.png|250px|thumb| | [[Файл:480px-Cornu Spiral.svg.png|250px|thumb| | ||
| − | + | Спіраль Корню (''x'',''y'')=(''C''(''t''), ''S''(''t'')). Спіраль збігається до центрів отворів при <math>t \rightarrow +\infty</math>.]] | |
| − | + | ||
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | == | + | =Функція помилок= |
| + | '''функція помилок''' | ||
| + | : <math>\operatorname{erf}\,x = \frac{2}{\sqrt{\pi}}\int\limits_0^x e^{-t^2}\,dt</math>. | ||
| − | + | '''Додаткова функція помилок''': | |
| − | + | : <math>\operatorname{erfc}\,x = 1-\operatorname{erf}\,x = \frac{2}{\sqrt{\pi}} \int\limits_x^{\infty} e^{-t^2}\,dt</math>. | |
| − | : | + | '''Комплексна функція помилок''': |
| − | + | ||
| − | + | : <math>w(x) = e^{-x^2}\operatorname{erfc}\,(-ix)</math>. | |
| − | + | == Властивості == | |
| − | + | * : | |
| − | + | : <math>\operatorname{erf}\,(-x) = -\operatorname{erf}\,x.</math> | |
| − | + | ||
| − | : <math> | + | * |
| + | : <math>\operatorname{erf}\,\bar{x} = \overline{\operatorname{erf}\,x} </math> | ||
| − | + | * | |
| + | : <math>\operatorname{erf}\,x= \frac{2}{\sqrt{\pi}}\sum_{n=0}^\infin\frac{(-1)^n x^{2n+1}}{n! (2n+1)} =\frac{2}{\sqrt{\pi}} \left(x-\frac{x^3}{3}+\frac{x^5}{10}-\frac{x^7}{42}+\frac{x^9}{216}-\ \cdots\right)</math> | ||
| − | + | * | |
| + | : <math>\operatorname{erf}\,x= \frac{2}{\sqrt{\pi}}\sum_{n=0}^\infin\left(x \prod_{i=1}^n{\frac{-(2i-1) x^2}{i (2i+1)}}\right) = \frac{2}{\sqrt{\pi}} \sum_{n=0}^\infin \frac{x}{2n+1} \prod_{i=1}^n \frac{-x^2}{i}</math> | ||
| + | поскольку <math>\frac{-(2i-1) x^2}{i (2i+1)}</math> — співмножник, перетворюючий <math>i</math>-й член ряда в <math>(i+1)</math>-й, рахуючи першим членом <math>x</math>. | ||
| − | |||
| − | |||
| − | |||
| − | == | + | == Асимптотичний розклад == |
| − | + | ||
| − | + | При великих <math>x</math> полезно [[асимптотичний разклад]] для додаткової функції помилок: | |
| − | + | : <math>\operatorname{erfc}\,x = \frac{e^{-x^2}}{x\sqrt{\pi}}\left [1+\sum_{n=1}^\infty (-1)^n \frac{1\cdot3\cdot5\cdots(2n-1)}{(2x^2)^n}\right ]=\frac{e^{-x^2}}{x\sqrt{\pi}}\sum_{n=0}^\infty (-1)^n \frac{(2n)!}{n!(2x)^{2n}}.\,</math> | |
| − | {{ | + | |
| − | == | + | == Функції == |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | |||
| − | |||
| − | + | ||
| + | : <math>\operatorname{erf}\,x= | ||
| + | \frac{2x}{\sqrt{\pi}}\,_1F_1\left(\frac{1}{2},\frac{3}{2},-x^2\right).</math> | ||
| + | |||
| + | |||
| + | |||
| + | : <math>\operatorname{erf}\,x=\operatorname{sign}\,x\,P\left(\frac{1}{2}, x^2\right)={\operatorname{sign}\,x \over \sqrt{\pi}}\gamma\left(\frac{1}{2}, x^2\right).</math> | ||
| + | |||
| + | === Узагальнені функції помилок === | ||
| + | |||
| + | |||
| + | |||
| + | <math>E_n(x) = \frac{n!}{\sqrt{\pi}} \int\limits_0^x e^{-t^n}\,dt | ||
| + | =\frac{n!}{\sqrt{\pi}}\sum_{p=0}^\infin(-1)^p\frac{x^{np+1}}{(np+1)p!}\,.</math> | ||
| + | |||
| + | |||
| + | * <math>E_0(x)</math> — прямая линия, проходящая через начало координат: <math>E_0(x)=\frac{x}{e \sqrt{\pi}}</math> | ||
| + | * <math>E_2(x)</math> — функция ошибок <math>\operatorname{erf}\,x</math>. | ||
| + | |||
| + | |||
| + | |||
| + | <math>E_n(x) = \frac{x\left(x^n\right)^{-1/n}\Gamma(n)\left(\Gamma\left(\frac{1}{n}\right)-\Gamma\left(\frac{1}{n},x^n\right)\right)}{\sqrt\pi}, | ||
| + | \quad \quad | ||
| + | x>0</math> | ||
| + | |||
| + | |||
| + | |||
| + | <math>\operatorname{erf}\,x = 1 - \frac{\Gamma\left(\frac{1}{2},x^2\right)}{\sqrt\pi}</math> | ||
| + | |||
| + | === Інтеровні інтеграли додаткової функції помилок === | ||
| + | |||
| + | |||
| + | <math> | ||
| + | i^n\,\operatorname{erfc}\,z = \int\limits_z^\infty i^{n-1}\,\operatorname{erfc}\,\zeta\,d\zeta.\, | ||
| + | </math> | ||
| + | |||
| + | |||
| + | <math> | ||
| + | i^n\,\operatorname{erfc}\,z | ||
| + | = | ||
| + | \sum_{j=0}^\infty \frac{(-z)^j}{2^{n-j}j!\,\Gamma \left( 1 + \frac{n-j}{2}\right)}\,, | ||
| + | </math> | ||
| + | |||
| + | <math> | ||
| + | i^{2m}\,\operatorname{erfc}\,(-z) | ||
| + | = -i^{2m}\,\operatorname{erfc}\,z | ||
| + | + \sum_{q=0}^m \frac{z^{2q}}{2^{2(m-q)-1}(2q)!(m-q)!} | ||
| + | </math> | ||
| + | |||
| + | |||
| + | |||
| + | <math> | ||
| + | i^{2m+1}\,\operatorname{erfc}\,(-z) | ||
| + | =i^{2m+1}\,\operatorname{erfc}\,z | ||
| + | + \sum_{q=0}^m \frac{z^{2q+1}}{2^{2(m-q)-1}(2q+1)! (m-q)!}\,. | ||
| + | </math> | ||
Версія за 21:29, 20 травня 2010
Інтеграли Френеля S(x) и C(x) — це спеціальні функції, названі на честь Огюстена Жана Френеля і використовуються в оптиці. Вони виникають при розрахунку дифракції Френеля і визначаються як
- Неможливо розібрати вираз (невідома помилка): S(x)=\int\limits_0^x \sin(t^2)\,dt,\quad C(x)=\int\limits_0^x \cos(t^2)\,dt.
Параметричний графік S(x) и C(x) дає криву на площині, яка має назву спіраль Корню
Зміст
Розклад в ряд
Інтеграли Френеля можуть бути представлені степеневими рядами, збіжними при всіх x:
- Неможливо розібрати вираз (невідома помилка): S(x)=\int\limits_0^x \sin(t^2)\,dt=\sum_{n=0}^{\infin}(-1)^n\frac{x^{4n+3}}{(4n+3)(2n+1)!},
- Неможливо розібрати вираз (невідома помилка): C(x)=\int\limits_0^x \cos(t^2)\,dt=\sum_{n=0}^{\infin}(-1)^n\frac{x^{4n+1}}{(4n+1)(2n)!}.
Рівняння 7.3.1 — 7.3.2</ref> використовують в якості аргумента тригонометричних підінтегральних функцій Неможливо розібрати вираз (невідома помилка): \frac{\pi}{2}t^2
.
Спіраль Корню
Функція помилок
функція помилок
- Неможливо розібрати вираз (невідома помилка): \operatorname{erf}\,x = \frac{2}{\sqrt{\pi}}\int\limits_0^x e^{-t^2}\,dt
.
Додаткова функція помилок:
- Неможливо розібрати вираз (невідома помилка): \operatorname{erfc}\,x = 1-\operatorname{erf}\,x = \frac{2}{\sqrt{\pi}} \int\limits_x^{\infty} e^{-t^2}\,dt
.
Комплексна функція помилок:
- Неможливо розібрати вираз (невідома помилка): w(x) = e^{-x^2}\operatorname{erfc}\,(-ix)
.
Властивості
- :
- Неможливо розібрати вираз (невідома помилка): \operatorname{erf}\,(-x) = -\operatorname{erf}\,x.
- Неможливо розібрати вираз (невідома помилка): \operatorname{erf}\,\bar{x} = \overline{\operatorname{erf}\,x}
- Неможливо розібрати вираз (невідома помилка): \operatorname{erf}\,x= \frac{2}{\sqrt{\pi}}\sum_{n=0}^\infin\frac{(-1)^n x^{2n+1}}{n! (2n+1)} =\frac{2}{\sqrt{\pi}} \left(x-\frac{x^3}{3}+\frac{x^5}{10}-\frac{x^7}{42}+\frac{x^9}{216}-\ \cdots\right)
- Неможливо розібрати вираз (невідома помилка): \operatorname{erf}\,x= \frac{2}{\sqrt{\pi}}\sum_{n=0}^\infin\left(x \prod_{i=1}^n{\frac{-(2i-1) x^2}{i (2i+1)}}\right) = \frac{2}{\sqrt{\pi}} \sum_{n=0}^\infin \frac{x}{2n+1} \prod_{i=1}^n \frac{-x^2}{i}
поскольку Неможливо розібрати вираз (невідома помилка): \frac{-(2i-1) x^2}{i (2i+1)}
— співмножник, перетворюючий Неможливо розібрати вираз (невідома помилка): i
-й член ряда в Неможливо розібрати вираз (невідома помилка): (i+1) -й, рахуючи першим членом Неможливо розібрати вираз (невідома помилка): x .
Асимптотичний розклад
При великих Неможливо розібрати вираз (невідома помилка): x
полезно асимптотичний разклад для додаткової функції помилок:
- Неможливо розібрати вираз (невідома помилка): \operatorname{erfc}\,x = \frac{e^{-x^2}}{x\sqrt{\pi}}\left [1+\sum_{n=1}^\infty (-1)^n \frac{1\cdot3\cdot5\cdots(2n-1)}{(2x^2)^n}\right ]=\frac{e^{-x^2}}{x\sqrt{\pi}}\sum_{n=0}^\infty (-1)^n \frac{(2n)!}{n!(2x)^{2n}}.\,
Функції
- Неможливо розібрати вираз (невідома помилка): \operatorname{erf}\,x= \frac{2x}{\sqrt{\pi}}\,_1F_1\left(\frac{1}{2},\frac{3}{2},-x^2\right).
- Неможливо розібрати вираз (невідома помилка): \operatorname{erf}\,x=\operatorname{sign}\,x\,P\left(\frac{1}{2}, x^2\right)={\operatorname{sign}\,x \over \sqrt{\pi}}\gamma\left(\frac{1}{2}, x^2\right).
Узагальнені функції помилок
Неможливо розібрати вираз (невідома помилка): E_n(x) = \frac{n!}{\sqrt{\pi}} \int\limits_0^x e^{-t^n}\,dt =\frac{n!}{\sqrt{\pi}}\sum_{p=0}^\infin(-1)^p\frac{x^{np+1}}{(np+1)p!}\,.
- Неможливо розібрати вираз (невідома помилка): E_0(x)
— прямая линия, проходящая через начало координат: Неможливо розібрати вираз (невідома помилка): E_0(x)=\frac{x}{e \sqrt{\pi}}
- Неможливо розібрати вираз (невідома помилка): E_2(x)
— функция ошибок Неможливо розібрати вираз (невідома помилка): \operatorname{erf}\,x
.
Неможливо розібрати вираз (невідома помилка): E_n(x) = \frac{x\left(x^n\right)^{-1/n}\Gamma(n)\left(\Gamma\left(\frac{1}{n}\right)-\Gamma\left(\frac{1}{n},x^n\right)\right)}{\sqrt\pi}, \quad \quad x>0
Неможливо розібрати вираз (невідома помилка): \operatorname{erf}\,x = 1 - \frac{\Gamma\left(\frac{1}{2},x^2\right)}{\sqrt\pi}
Інтеровні інтеграли додаткової функції помилок
Неможливо розібрати вираз (невідома помилка): i^n\,\operatorname{erfc}\,z = \int\limits_z^\infty i^{n-1}\,\operatorname{erfc}\,\zeta\,d\zeta.\,
Неможливо розібрати вираз (невідома помилка): i^n\,\operatorname{erfc}\,z = \sum_{j=0}^\infty \frac{(-z)^j}{2^{n-j}j!\,\Gamma \left( 1 + \frac{n-j}{2}\right)}\,,
Неможливо розібрати вираз (невідома помилка): i^{2m}\,\operatorname{erfc}\,(-z) = -i^{2m}\,\operatorname{erfc}\,z + \sum_{q=0}^m \frac{z^{2q}}{2^{2(m-q)-1}(2q)!(m-q)!}
Неможливо розібрати вираз (невідома помилка): i^{2m+1}\,\operatorname{erfc}\,(-z) =i^{2m+1}\,\operatorname{erfc}\,z + \sum_{q=0}^m \frac{z^{2q+1}}{2^{2(m-q)-1}(2q+1)! (m-q)!}\,.