Симплекс-метод розв’язування задач ЛП. Оптимальний розв’язок. Критерій оптимальності плану
Зміст
Симплексний метод
Цей метод уможливлює направлений перебір опорних планів, тобто перехід від одного плану до іншого, який є хоча б не гіршим від попереднього за значенням функціонала. Отже, окремим питанням стає вибір вектора, який необхідно вводити в базис при здійсненні ітераційної процедури симплексного методу.
Розглянемо задачу лінійного програмування, записану в канонічній формі:
Не порушуючи загальності, допустимо, що система рівнянь містить перші m одиничних векторів. Отримаємо:
Розглянемо задачу лінійного програмування
Допустимо, що вона має опорні плани і вони є невиродженими. Розглянемо початковий опорний план виду
Такому плану відповідає розклад за базисними векторами
та значення функціонала:
Кожен з векторів Неможливо розібрати вираз (невідома помилка): A_1,A_2,..,A_n
можна розкласти за векторами базису, причому у єдиний спосіб:
тому такому розкладу відповідатиме і єдине значення функціонала:
Позначимо через Неможливо розібрати вираз (невідома помилка): c_j
коефіцієнт функціонала, що відповідає вектору Неможливо розібрати вираз (невідома помилка): A_j , та позначимо Неможливо розібрати вираз (невідома помилка): \bigtriangleup_j=F_j-c_j
. (їх називають оцінками відповідних векторів плану) Неможливо розібрати вираз (невідома помилка): (j=1,n)
Теорема 1
Якщо для деякого вектора Неможливо розібрати вираз (невідома помилка): A_j
виконується умова Неможливо розібрати вираз (невідома помилка): F_j-c_j<0 , то план Неможливо розібрати вираз (невідома помилка): X_0 не є оптимальним і можна відшукати такий план Х, для якого виконуватиметься нерівність Неможливо розібрати вираз (невідома помилка): F(X)>F(X_0).
Якщо розглядається задача на відшукання мінімального значення цільової функції, то формулюється така теорема.
Теорема 2
Якщо для деякого вектора Неможливо розібрати вираз (невідома помилка): A_j
виконується умова Неможливо розібрати вираз (невідома помилка): F_j-c_j>0 ,то план Неможливо розібрати вираз (невідома помилка): X_0 не є оптимальним і можна побудувати такий план Х, для якого виконуватиметься нерівність Неможливо розібрати вираз (невідома помилка): F(X)<F(X_0).
Наслідок:
(умова оптимальності плану задачі максимізації): якщо для деякого плану Неможливо розібрати вираз (невідома помилка): X_0
розклад всіх векторів Неможливо розібрати вираз (невідома помилка): A_j(j=1,n) у даному базисі задовольняє умову:
є оптимальним розв’язком задачі лінійного програмування (1)-(3).
(умова оптимальності плану задачі мінімізації): якщо для деякого плану Неможливо розібрати вираз (невідома помилка): X_0
розклад всіх векторів Неможливо розібрати вираз (невідома помилка): A_j(j=1,n) у даному базисі задовольняє умову
то план Неможливо розібрати вираз (невідома помилка): X_0
є оптимальним розв’язком задачі лінійного програмування.
Отже, для того, щоб план задачі лінійного програмування був оптимальним, необхідно і достатньо, щоб його оцінки Неможливо розібрати вираз (невідома помилка): \bigtriangleup_j=F_j-c_j
були невід’ємними для задачі на максимум та недодатними для задачі на мінімум.
Приклад
Знайти значення змінних Неможливо розібрати вираз (невідома помилка): x_1,x_2 , при яких функція Неможливо розібрати вираз (невідома помилка): Q=5x_1+6x_2
приймає максимальне значення, за умови наступних обмежень:
Крок: 1
Позбудемося нерівностей в обмеженнях, ввівши в обмеження 1, 2, 3 невід'ємні балансові змінні Неможливо розібрати вираз (невідома помилка): s_1,s_2,s_3
Крок: 2
Шукаємо в системі обмежень базисні змінні.
З останньої системи обмежень можна виділити базисні змінні Неможливо розібрати вираз (невідома помилка): s_1,s_2,s_3
.
Тепер ми можемо сформувати початкову симплекс-таблицю.
Крок: 3
Початкова симплекс-таблиця
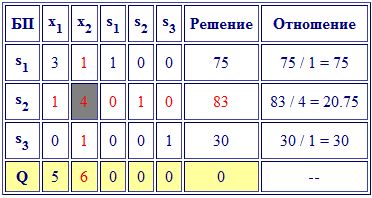
Iтерація 1
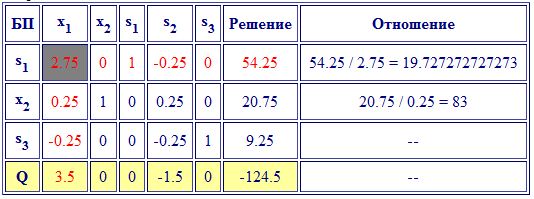
Iтерація 2
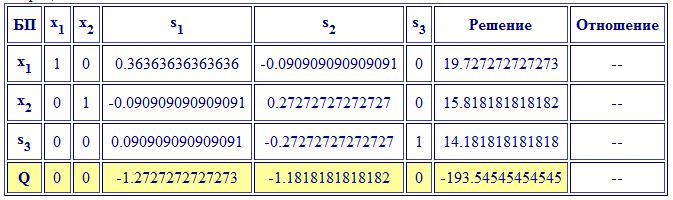
Досягнуто оптимальне рішення, тому що в рядку цільової функції немає позитивних коефіцієнтів.
Відповідь: Оптимальне значення функції Q (x) = 193.54545454545 досягається в точці з координатами
