Одноетапна Р-модель з імовірнісними обмеженнями. Алгоритм побудови розв’язувального правила. Приклад.
Позначимо через Неможливо розібрати вираз (невідома помилка): \omega
стан природи (елементарну подію), а через Неможливо розібрати вираз (невідома помилка): \Omega ‒ множину станів природи (елементарних подій). Нехай для кожного Неможливо розібрати вираз (невідома помилка): \omega \in \Omega на деякій множині Х задані множини Неможливо розібрати вираз (невідома помилка): G_0 (\omega), (G_0(\omega)\ne X) i Неможливо розібрати вираз (невідома помилка): G_i (\omega), (i=1,2,...,m)
Розглянемо наступну загальну Р-модель з ймовірнісними умовами.
Потрібно визначити Неможливо розібрати вираз (невідома помилка): x(\omega)\in X ,що максимізує ймовірність попадання в Неможливо розібрати вираз (невідома помилка): G_0(\omega)
умов, що ймовірність попадання в Неможливо розібрати вираз (невідома помилка): G_i(\omega) не менша заданого числа Неможливо розібрати вираз (невідома помилка): \alpha_i
. Таким чином, розв'язок визначається у вигляді випадкового вектора і розв'язуване правило заздалегідь не задане.
Формально задача записується у наступному вигляді:
Неможливо розібрати вираз (невідома помилка): P{x(\omega)\in G_0(\omega)}\rightarrow sup,
(4.1)
Неможливо розібрати вираз (невідома помилка): P{x(\omega)\in G_i(\omega)}\ge\alpha_i,i=1,2,...,m
(4.2)
Введемо характеристичні функції множин Неможливо розібрати вираз (невідома помилка): G_i (\omega)
Неможливо розібрати вираз (невідома помилка): \psi_i (\omega,x)= \begin{cases}1, x\in G_i(\omega),\\ 0, x \ne G_i(\omega),\\ i=1,2,...,m \end{cases}
Тоді:
Неможливо розібрати вираз (невідома помилка): P{x(\omega)\in G_i(\omega)}=\int\limits_\Omega \psi_i(\omega,x(\omega)) dp ,
Де р‒ ймовірнісна міра, що визначає ймовірнісний простір Неможливо розібрати вираз (невідома помилка): ( \Omega,\Sigma , p ).
Нехай міра р неперервна.
Задача (4.1)-(4.2) прийме вигляд:
Неможливо розібрати вираз (невідома помилка): \int\limits_\Omega \psi_0(\omega,x) dp \rightarrow sup,
Неможливо розібрати вираз (невідома помилка): \int\limits_\Omega \psi_i(\omega,x) dp\ge\alpha_i,i=1,2,...,m
Візьмемо m=2.
Сформулюємо умови сумісності задачі (4.1)-(4.2). Введемо 2 множини:
Неможливо розібрати вираз (невідома помилка): \Omega ' = {\omega:G_1(\omega)\cap G_2(\omega)\ne \varnothing} , Неможливо розібрати вираз (невідома помилка): \Omega '' = {\omega:G_1(\omega)\cap G_2(\omega)= \varnothing} .
Теорема 4.1. Для сумісності задачі (4.1)-(4.2) (при m=2) необхідно і достатньо, щоб:
Неможливо розібрати вираз (невідома помилка): \begin{cases}\ \alpha_1 \le 1, \alpha_2 \le 1,\\ \alpha_1+\alpha_2+P\Omega '' \le 2 \end{cases}
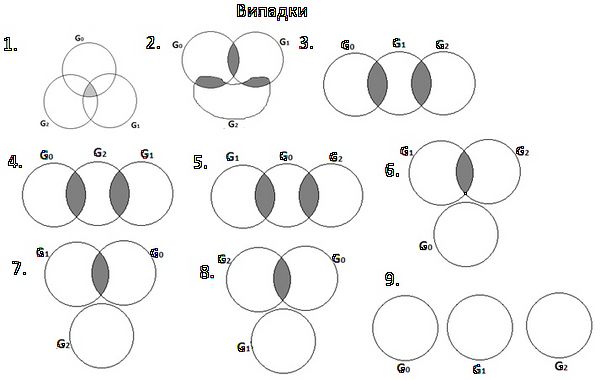
Можна вказати наступні дев'ять попарно несумісних ситуацій взаємного розміщення множин Неможливо розібрати вираз (невідома помилка): G_i, i=0,1,2,
які показують всі можливі випадки.
1. Неможливо розібрати вираз (невідома помилка): G_1\cap G_2 \cap G_0 \ne \varnothing
2. Неможливо розібрати вираз (невідома помилка): G_1\cap G_2 \cap G_0 = \varnothing, G_1\cap G_2 = \varnothing, G_1\cap G_0 \ne \varnothing
3. Неможливо розібрати вираз (невідома помилка): G_1\cap G_2 \cap G_0 = \varnothing, G_1\cap G_2 \ne \varnothing, G_1\cap G_0 \ne \varnothing
4. Неможливо розібрати вираз (невідома помилка): G_1\cap G_2 \ne \varnothing, G_1\cap G_0 = \varnothing, G_2\cap G_0 \ne \varnothing
5. Неможливо розібрати вираз (невідома помилка): G_1\cap G_2 = \varnothing, G_1\cap G_0 \ne \varnothing, G_2\cap G_0 \ne \varnothing
6. Неможливо розібрати вираз (невідома помилка): G_1\cap G_2 = \varnothing, G_1\cap G_0 = \varnothing, G_2\cap G_0 = \varnothing
7. Неможливо розібрати вираз (невідома помилка): G_1\cap G_2 = \varnothing, G_1\cap G_0 \ne \varnothing, G_2\cap G_0 = \varnothing
8. Неможливо розібрати вираз (невідома помилка): G_1\cap G_2 = \varnothing, G_1\cap G_0 = \varnothing, G_2\cap G_0 \ne \varnothing
9. Неможливо розібрати вираз (невідома помилка): G_1\cap G_2 = G_1\cap G_0 = G_2\cap G_0 = \varnothing
Нехай Неможливо розібрати вираз (невідома помилка): \Omega_i
‒ множина тих Неможливо розібрати вираз (невідома помилка): \omega \in \Omega при яких реалізується і-та ситуація і Неможливо розібрати вираз (невідома помилка): p_i=P\Omega_i, i=1,...,9.
Розчленуємо множину Неможливо розібрати вираз (невідома помилка): U=\bigcup\limits_{k=0}^2 G_k
на 7 підмножин, які попарно не перетинаються, наступним чином:
Неможливо розібрати вираз (невідома помилка): U^1=G_0 \cap G_1 \cap G_2 ,
Неможливо розібрати вираз (невідома помилка): U^2=(G_0 \cap G_1)\setminus G_0 \cap G_1\cap G_2 ,
Неможливо розібрати вираз (невідома помилка): U^3=(G_0 \cap G_2) \setminus G_0 \cap G_1\cap G_2 ,
Неможливо розібрати вираз (невідома помилка): U^4=(G_1 \cap G_2)\setminus G_0 \cap G_1\cap G_2 ,
Неможливо розібрати вираз (невідома помилка): U^5=G_0\setminus [(G_0\cap G_1)\cup (G_0 \cap G_2)] ,
Неможливо розібрати вираз (невідома помилка): U^6=G_1 \setminus [(G_0\cap G_1)\cup (G_1 \cap G_2)] ,
Неможливо розібрати вираз (невідома помилка): U^7=G_2 \setminus [(G_0\cap G_2)\cup (G_1 \cap G_2)] ,
Очевидно, що Неможливо розібрати вираз (невідома помилка): U=\bigcup\limits_{j=0}^7 U^j; U^i \cap U^j = \varnothing
Введемо змінні Неможливо розібрати вираз (невідома помилка): u_i^j
Неможливо розібрати вираз (невідома помилка): u_i^j=P{x\in U^j | i}
Неможливо розібрати вираз (невідома помилка): u_i^j
- умовна ймовірність події Неможливо розібрати вираз (невідома помилка): x \in U^j за умови, що має місце і-та ситуація взаємного розміщення множин Неможливо розібрати вираз (невідома помилка): G_k
.