Умова цілочисельності опорного плану

Теорема

Теорема 5.3. Якщо всі запаси Неможливо розібрати вираз (невідома помилка): a_i (i= \bar{(1,n)}

і всі потреби  Неможливо розібрати вираз (невідома помилка): b_j, (j= \bar{(1,n)}
є невід’ємними цілими числами, то будь-який опорний план складається із значень, що є цілими числами.

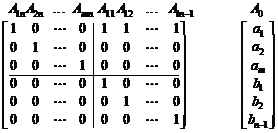
Доведення. Компоненти кожної системи із m+n-1 лінійно не-залежних (базисних) векторів можуть бути подані у вигляді три-кутної матриці. Нехай розглядається задача (5.1)—(5.4). Матриця з перших m+n-1 компонент базисних векторів системи (5.2), (5.3) матиме вигляд:

(5.19) Перша половина матриці від Неможливо розібрати вираз (невідома помилка): A_{1n}...A_{mn}

це m, а Неможливо розібрати вираз (невідома помилка): A_{11}...A_{1}{n-1}
це n-1.

Розв’язування системи, що визначається (5.19), включатиме лише дії додавання та віднімання, і, оскільки Неможливо розібрати вираз (невідома помилка): a_i (i= \bar{(1,n)}

 та Неможливо розібрати вираз (невідома помилка): b_j, (j= \bar{(1,n)}
 у постановці транспортної задачі є цілими числами, то значення змінних також будуть цілими числами.