Мережі Петрі
Зміст
Мережа Петрі
Мережа Петрі – це графічний і математичний засіб моделювання систем і процесів.
Графічно представляється у вигляді дводольного орієнтованого мультиграфу з маркерами («фішками») (маркований орієнтований граф), який має дві групи вершин: позиції та переходи. Позиції можуть бути пустими або маркованими та визначають <стан> мережі. Переходи визначають дії. Орієнтовані ребра графу задають зв'язки між позиціями та переходами. Процес функціонування мережі Петрі полягає в послідовному «виконанні» переходів, та відповідному перерахункові кількості «фішок» у позиціях. Дуги можуть бути кратними, коли два вузли з'єднані більше ніж однією дугою однакового напрямку. Альтернативно, для відображення кратності дуг може використовуватися функція «ваги» дуг.
Як правило, мережами Петрі моделюють паралельні (синхронні та асинхронні) системи і процеси. Спочатку запропоновані в докторській дисертації Карла Петрі в 1962 році вони одержали подальший розвиток у роботах таких вчених як Тадао Мурата, Курт Йенсен, Віталій Котов, Анатолій Слєпцов. В останні часи проводиться щорічна конференція «Застосування і теорія мереж Петрі», видається в Боні інформаційний бюлетень «Новини мереж Петрі» (Petri Net Newsletter), відомо декілька сот моделюючих систем для різних програмно-апаратних платформ, існують реалізації процесорів мереж Петрі. Галузі застосування мереж Петрі включають дослідження телекомунікаційних мереж, мережних протоколів, обчислювальних систем і обчислювальних процесів, виробничих і організаційних систем.
Прості мережі Петрі
Мережа Петрі є орієнтованим дводольним графом, який має чотири базових елементи: вузди, або місця(places), переходи(transitions), дуги(arcs) і маркери(tokens). Вузли позначаються кружками і визначають стан, в якому може знаходитись мережа або її частина. Переходи-це активні елементи мережі, які позначають дії, виконувані під час спрацювання переходів. Для того щоб перехід міг спрацювати, необхідне виконання певних умов, які визначаються наявністю маркерів у вузлах мережі, з'єднаних з переходом. Якщо умови настання подій виконано, то вважають, що перехід збуджений. Переходи позначаються короткими вертикальними або горизонтальними лініями. Вузли та переходи з'єднуються орієнтованими ребрами (дугами). Два вузли або два переходи з'єднуватись дугами не можуть.
Функціонування мережі Петрі можна описати так: вузли як певні умови, а переходи-як події. Таким чином, стан мережі в кожний момент часу задається системою умов. Для зручності задання умов мережі Петрі вводяться маркери(фішки), які зображуються крапками всередині вузлів. Виникнення певної комбінації маркерів у вузлах приводить до настання деякої події, яка у свою чергу викликає зміну стану умов мережі. Стан маркування або стан мережі Петрі визначаеться сукупністю маркерів кожного окремого вузда мережі.
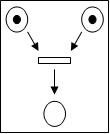
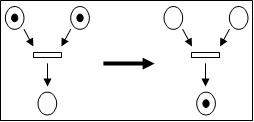
Перехід, в якого всі вхвдні вузли містять маркери, називається збудженим (Рис.1). Збуджений перехід може спрацювати, після чого всі маркери із вхідних вузлів переходу перемістятся у вихідні(Рис.2). Таким чином, настає подія, яка змінює стан мережі.
Якщо одночасно збуджуються кілька переходів мережі, виникає невизначеність, тому одночасне спрацювання кількох переходів у мережі Петрі неможливе, тобто переходи спрацьовують послідовно, миттєво. Незважаючи на те, що маркери змінюють своє положення у вузлах, прості мережі Петрі- це статичні моделі, в яких не враховується динаміка в часі (зміна станів мережі не залежить від моментів часу). Для того щоб за допомогою мережі Петрі відтворити динаміку роботи деякої детермінованої динамічної системи в часі, необхідно зазначати моменти спрацьовування переходів. Такі можливості мають тільки розширення мереж Петрі, в яких спрацювання переходів здійснюється в задані моменти модельного часу з деяким постійним кроком дельта(т).
Дослідження мережі Петрі
Основні методи дослідження мереж Петрі:
- Дерево досягальності,
- Графічний,
- Аналітичний,
- За допомогою еквівалентних перетвореннь.
Взагалі, мережі Петрі досліджують на такі властивості:
- Безпечність — досліджує виконання умови що кількість «фішок» в позиції не перевищує 1;
- Обмеженість — досліджує виконання умови що кількість «фішок» в позиції не перевищує заданого числа,
- Зберігальність — досліджує виконання умови що кількість «фішок» в мережі не змінюється,
- Оберненість — для довільного досяжного стану досліджується існування послідовності виконань переходів яка повертає мережу в початковий стан),
- Активність переходів — досліджує можливість виконання певних переходів та наявність тупиків — станів у яких переходи не дозволені та для яких неможливо досягти стану в якому ці переходи дозволені,
- Досяжність маркування — досліджує існування послідовності виконань переходів при якій можна досягнути задане маркування,
- Покриття — досліджує існування послідовності виконань переходів при якій можна досягнути маркування що покриває, тобто є більшим за задане маркування.
Умова зберігальності може бути послаблена, для чого вводять поняття функції ваги:
- Неможливо розібрати вираз (невідома помилка): \mathbf W:\qquad(\mathbf T \times \mathbf P) \cup (\mathbf P \times \mathbf T) \to \mathbb N \cup \{0\}
яка залишається постійною під час роботи.
Більшість досліджень мереж Петрі можна звести до побудови дерева досяжності.
Комп'ютерні моделюючі системи
Pndpi, Tina, Design/CPN
Список використаної літератури
1.
2. Зайцев Д.А. Мережі Петрі і моделювання систем: Навчальній посібник // , Одеса 2006
3. Зайцев Д.А. Математичні моделі дискретних систем: Навчальний посібник // Одеса: ОНАЗ ім. О.С. Попова, 2004. – 40 с.
4. Математичні основи теорії телекомунікаційних систем / Підручник за загальною редакцію В.В. Поповського. – Харків, ТОВ «Компанія СМІТ», 2006. – 564 с.
5. Питерсон Дж. Теория сетей Петри и моделирование систем. – М. Мир, 1984. – 264 с.
6. Котов В.Е. Сети Петри. – М.: Наука, 1984. – 160 с.
7. Ачасова С.М., Бандман О.Л. Корректность параллельных вычислительных процессов. – Н.: Наука, 1990. – 253 с.
8. Слепцов А.И., Юрасов А.А. Автоматизация проектирования управляющих систем гибких автоматизированных производств / Под ред. Б.Н.Малиновского. – К.: Технiка, 1986. – 160 с.