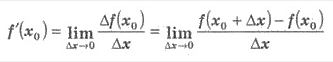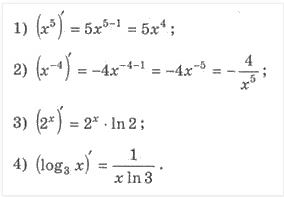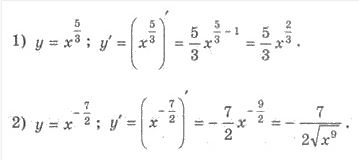Означення похідної
Означення похідної функції. Геометричний і фізичний зміст
Означення похідної в точці
Похідною функції у = f(х) в точці х0 називають границю відношення приросту функції ∆f(x0) в точці х0 до приросту аргументу ∆х, коли приріст аргументу прямує до нуля, тобто
Функцію у = f(х), що має похідну в точці х0 називають диференційованою в цій точці. Якщо функція у = f(х) має прохідну в кожній точці деякого проміжку, то кажуть, що ця функція диференційована на даному проміжку. Операцію взяття (знаходження) похідної називають диференціюванням функції. У курсі шкільної математики похідні знаходять в основному, не за означенням, а використовуючи таблицю похідних та правила знаходження похідних.
Похідною функції f(x) у точці х0називається границя (якщо вона існує) відношення приросту функції у точці х0до приросту аргументу Δх, якщо приріст аргументу прямує до нуля і позначається f'(x0). Дія знаходження похідної функції називається диференціюванням.
Похідна функції має такий фізичний зміст: похідна функції в заданій точці – швидкість зміни функції в заданій точці.
Похідна функції має такий геометричний зміст: похідна функції в заданій точці є кутовим коефіцієнтом дотичної до графіка функції в цій точці, тобто дорівнює тангенсу кута нахилу дотичної до графіка функції в заданій точці.
Запам’ятайте!
- Похідна функції у = x дорівнює одиниці;
- Похідна степеневої функції дорівнює показнику степеня, помноженому на основу в степені, на одиницю меншу; (похідна функції у = xn дорівнює добутку n іxn-1);
- Похідна функції у = 1/x дорівнює одиниці, поділеній на х2, узятій зі знаком мінус;
- Похідна функції у = √x для додатних х дорівнює 1/(2√x);
- Похідна функції синус х дорівнює косинусу х;
- Похідна функції косинус х дорівнює синусу х, взятому зі знаком мінус;
- Похідна функції тангенс х на її області визначення дорівнює одиниці, поділеній на квадрат косинуса х;
- Похідна функції котангенс х на її області визначення дорівнює одиниці, поділеній на квадрат синуса х, взятій зі знаком мінус;
- Похідна показникової функції у = ах дорівнює цій функції, помноженій на натуральний логарифм основи ах∙ ln а;
- Похідна функції у = ех дорівнює самій функції, тобто ех;
- Похідна логарифмічної функції у = logax на її області визначення дорівнює1/(х∙ ln а);
- Похідна функції у = ln x на її області визначення дорівнює одинці, поділеній на х .
Можна визначити похідні вищих порядків. Похідною n-го порядку (n-ною похідною) називається похідна від похідної (п – 1) порядку.
Таблиця похідних елементарних функцій
Приклад 1:
Розв'язання:
Приклад 2:
Розв'язання: