Основи векторної графіки
Основи створення векторної графіки
Як уже зазначалося, векторне графічне зображення складається з графічних примітивів – відрізків, кривих, ламаних, прямокутників, многокутників, овалів тощо (рис. 7.20).
На малюнку об’єкти можуть накладатися, утворюючи багатошарове зображення, в якому кожний окремий об’єкт розміщується у своєму шарі. Графічні примітиви є самостійними об’єктами, і їх можна змінювати незалежно від інших об’єктів цього зображення.
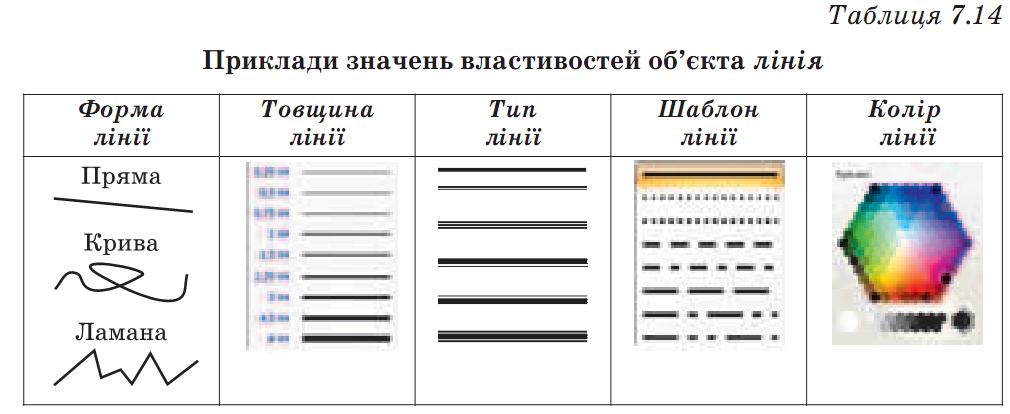
Одним із графічних примітивів векторного малюнка є лінія. Лінія може бути замкненою або незамкненою. Об’єкт лінія характеризується такими властивостями: форма, товщина, тип, шаблон, колір та ін. Можливі значення цих властивостей наведено в таблиці 7.14.
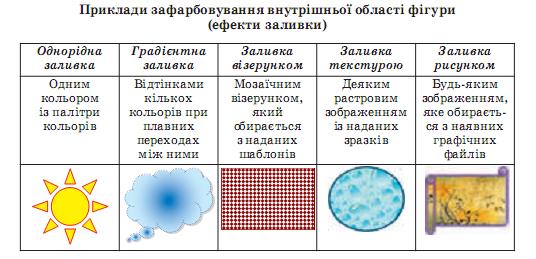
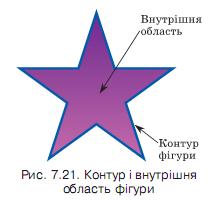 Іншими графічними примітивами є фігури, які обмежені замкненими лініями. Ці замкнені лінії утворюють контур фігури, а частина площини, яку вони обмежують, – внутрішню область фігури (рис. 7.21). Внутрішня область фігури може бути зафарбована. При цьому можна використати один із п’яти способів (ефектів) заливки: од норідна, градієнтна, візерунок, текстура, рисунок (табл.7.15).
Іншими графічними примітивами є фігури, які обмежені замкненими лініями. Ці замкнені лінії утворюють контур фігури, а частина площини, яку вони обмежують, – внутрішню область фігури (рис. 7.21). Внутрішня область фігури може бути зафарбована. При цьому можна використати один із п’яти способів (ефектів) заливки: од норідна, градієнтна, візерунок, текстура, рисунок (табл.7.15).
При зберіганні векторного зображення у файлі всі його об’єкти описуються математично, за допомогою векторів. Тому цей вид графіки й отримав таку назву.
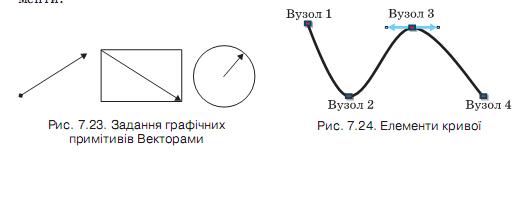
У векторному зображенні відрізок задається вектором, початок якого є одним із кінців відрізка, а його кінець – іншим кінцем відрізка (рис. 7.23). Прямокутник – вектором, початок якого є однією з вершин прямокутника, а кінець – протилежною вершиною. Коло задається вектором, початок якого є центр кола, а кінець – довільна точка кола. Контури фігур довільної форми та криві лінії описуються сукупністю векторів.
Кожна крива має кілька опорних точок, які називаються вузлами. Частина кривої, яка з’єднує два сусідніх вузла, називається сегментом. На рисунку 7.24. наведено приклад кривої, в якої чотири вузли і три сегменти.