Мережі Петрі

Мережа Петрі

Рис.1 Проста мережа Петрі з одним переходом, трьома вузлами, два з яких містять маркери

Мережа Петрі – це графічний і математичний засіб моделювання систем і процесів.

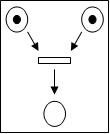
Графічно представляється у вигляді дводольного орієнтованого мультиграфу з маркерами («фішками») (маркований орієнтований граф), який має дві групи вершин: позиції та переходи. Позиції можуть бути пустими або маркованими та визначають <стан> мережі. Переходи визначають дії. Орієнтовані ребра графу задають зв'язки між позиціями та переходами. Процес функціонування мережі Петрі полягає в послідовному «виконанні» переходів, та відповідному перерахункові кількості «фішок» у позиціях. Дуги можуть бути кратними, коли два вузли з'єднані більше ніж однією дугою однакового напрямку. Альтернативно, для відображення кратності дуг може використовуватися функція «ваги» дуг.

Як правило, мережами Петрі моделюють паралельні (синхронні та асинхронні) системи і процеси. Спочатку запропоновані в докторській дисертації Карла Петрі в 1962 році вони одержали подальший розвиток у роботах таких вчених як Тадао Мурата, Курт Йенсен, Віталій Котов, Анатолій Слєпцов. В останні часи проводиться щорічна конференція «Застосування і теорія мереж Петрі», видається в Боні інформаційний бюлетень «Новини мереж Петрі» (Petri Net Newsletter), відомо декілька сот моделюючих систем для різних програмно-апаратних платформ, існують реалізації процесорів мереж Петрі. Галузі застосування мереж Петрі включають дослідження телекомунікаційних мереж, мережних протоколів, обчислювальних систем і обчислювальних процесів, виробничих і організаційних систем.

Комп'ютерні моделюючі системи

Pndpi, Tina, Design/CPN

Визначення

Мережа Петрі задається у вигляді маркованого дводольного орієнтованого графу. Розрізняють два види вершин:

• Позиції. P — множина позицій,
• Переходи. T — множина переходів.

Ребра називають дугами. Петлі в графі мереж Петрі неможливі, оскільки дуги можуть з'єднувати лише вершини різних типів (позиції та переходи). Позиції що з'єднані дугами з переходом називають вхідними та вихідними для цього переходу, відповідно до напрямку цих дуг.

Кожній позиції приписують деяке ціле додатнє число

Неможливо розібрати вираз (невідома помилка): \mu_p \in \mathbb{N} \cup \{0\}

що називається маркуванням. Сукупність маркувань всіх позицій можна записувати у вигляді вектора.

Таким чином, для того щоб задати мережу Петрі, необхідно задати пару

Неможливо розібрати вираз (невідома помилка): \left\langle\mathbf N, \mu_0 \right\rangle

де Неможливо розібрати вираз (невідома помилка): \mu_0 = \left\{\mu(p_1),\mu(p_2),...\mu(p_n)\right\}  — вектор маркування позицій, Неможливо розібрати вираз (невідома помилка): \mathbf N  — структура мережі Петрі:

Неможливо розібрати вираз (невідома помилка): \mathbf N = \left\langle\mathbf P, \mathbf T, \mathbf I, \mathbf O \right\rangle

.
де Неможливо розібрати вираз (невідома помилка): \mathbf P  — множина позицій, Неможливо розібрати вираз (невідома помилка): \mathbf T  — множина переходів, Неможливо розібрати вираз (невідома помилка): \mathbf I  — вхідна функція, Неможливо розібрати вираз (невідома помилка): \mathbf O  — вихідна функція.
Вхідна та вихідна функції задаються у вигляді множин комлектів позицій, які є вхідними та вихідними для заданого переходу:

Неможливо розібрати вираз (невідома помилка): \mathbf I = \left\{\mathbf I(t_j)\right\}

, Неможливо розібрати вираз (невідома помилка): \mathbf \mathbf I(t_j) = \left\{p_k\right\} .

Неможливо розібрати вираз (невідома помилка): \mathbf O = \left\{\mathbf O(t_j)\right\}

, Неможливо розібрати вираз (невідома помилка): \mathbf \mathbf O(t_j) = \left\{p_k\right\} .
Комплект — узагальнення множини, в якому допускається багаторазове включення однакових елементів. Для комплектів визначається операція кратності. Для запису функції кратності використовується символ #. Кратність вхідної (вихідної) позиції Неможливо розібрати вираз (невідома помилка): p_i

для переходу Неможливо розібрати вираз (невідома помилка): t_j
це кількість появ позиції Неможливо розібрати вираз (невідома помилка): p_i
у вхідному (вихідному) комплекті переходу Неможливо розібрати вираз (невідома помилка): t_j

Неможливо розібрати вираз (невідома помилка): \#(p_i, \mathbf I(t_j))

.
Альтернативною формою представлення вхідної та вихідної функції є задання множини дуг та окремого вектору кратності (ваги) дуг.
Виконання переходу можливе лише за наявності достатньої кількості «фішок» у його вхідних позиціях. Умова можливості виконання переходу Неможливо розібрати вираз (невідома помилка): t_j

Неможливо розібрати вираз (невідома помилка): \mu(p_i) \ge \;\#\left(p_i, \mathbf I(t_j)\right) \forall p_i\in\mathbf P

.
Результатом виконання переходу є зміна кількості «фішок» у вхідних та вихідних позиціях цього переходу, тобто зміна маркування (стану) мережі Петрі. Нове маркування Неможливо розібрати вираз (невідома помилка): \mu^{i+1}

визначається таким співвідношенням:

Неможливо розібрати вираз (невідома помилка): \mu^{i+1}(p_i) = \mu^i(p_i) - \#(p_i, \mathbf I(t_j)) + \#(p_i, \mathbf O(t_j))

,
де Неможливо розібрати вираз (невідома помилка): t_j  — перехід що виконується Неможливо розібрати вираз (невідома помилка): \mu^{i}(p_i)  — попереднє маркування.
Цей вираз дозволяє записати векторну функцію наступного стану, яка виражає наступне маркування мережі Петрі через попереднє маркування та перехід що виконується:

Неможливо розібрати вираз (невідома помилка): \mu^{i+1} = \delta\left(\mu^i, t_j\right)

.
Для заданої послідовності виконання переходів Неможливо розібрати вираз (невідома помилка): \sigma = \left\langle t_{j1}, t_{j2},... ,t_{jl}\right\rangle

використовується розширена функція наступного стану:

Неможливо розібрати вираз (невідома помилка): \mu^{i+l} = \delta\left(\mu^i, \sigma\right) = \delta\left(... \delta\left(\delta\left(\mu^i, t_{j1}\right), t_{j2}\right),... ,t_{jl}\right)

.

Виконання переходів є атомарним, тобто перехід змінює стан всіх вхідних та вихідних позицій однією дією, яка не може бути перервана виконанням іншого переходу. Виконання мереж Петрі в цілому є недетермінованим:

1. відразу декілька переходів можуть бути дозволеними, і кожен з них може бути виконаний
2. дозволені переходи не обов'язково виконуються. Дозволений перехід може бути виконаний.

Взагалі, мережі Петрі не розглядають поняття «часу» виконання переходу, а лише послідовність виконань. За допомогою мереж Петрі можна моделювати такі якості як:

• асинхронність,
• конфліктнісь,
• паралелізм.

Дослідження мережі Петрі

Основні методи дослідження мереж Петрі:

1. Дерево досягальності,
2. Графічний,
3. Аналітичний,
4. За допомогою еквівалентних перетвореннь.

Взагалі, мережі Петрі досліджують на такі властивості:

1. Безпечність — досліджує виконання умови що кількість «фішок» в позиції не перевищує 1;
2. Обмеженість — досліджує виконання умови що кількість «фішок» в позиції не перевищує заданого числа,
3. Зберігальність — досліджує виконання умови що кількість «фішок» в мережі не змінюється,
4. Оберненість — для довільного досяжного стану досліджується існування послідовності виконань переходів яка повертає мережу в початковий стан),
5. Активність переходів — досліджує можливість виконання певних переходів та наявність тупиків — станів у яких переходи не дозволені та для яких неможливо досягти стану в якому ці переходи дозволені,
6. Досяжність маркування — досліджує існування послідовності виконань переходів при якій можна досягнути задане маркування,
7. Покриття — досліджує існування послідовності виконань переходів при якій можна досягнути маркування що покриває, тобто є більшим за задане маркування.

Умова зберігальності може бути послаблена, для чого вводять поняття функції ваги:

Неможливо розібрати вираз (невідома помилка): \mathbf W:\qquad(\mathbf T \times \mathbf P) \cup (\mathbf P \times \mathbf T) \to \mathbb N \cup \{0\}

яка залишається постійною під час роботи.

Більшість досліджень мереж Петрі можна звести до побудови дерева досяжності.

Список використаної літератури

1.

2. Зайцев Д.А. Мережі Петрі і моделювання систем: Навчальній посібник // , Одеса 2006

3. Зайцев Д.А. Математичні моделі дискретних систем: Навчальний посібник // Одеса: ОНАЗ ім. О.С. Попова, 2004. – 40 с.

4. Математичні основи теорії телекомунікаційних систем / Підручник за загальною редакцію В.В. Поповського. – Харків, ТОВ «Компанія СМІТ», 2006. – 564 с.

5. Питерсон Дж. Теория сетей Петри и моделирование систем. – М. Мир, 1984. – 264 с.

6. Котов В.Е. Сети Петри. – М.: Наука, 1984. – 160 с.

7. Ачасова С.М., Бандман О.Л. Корректность параллельных вычислительных процессов. – Н.: Наука, 1990. – 253 с.

8. Слепцов А.И., Юрасов А.А. Автоматизация проектирования управляющих систем гибких автоматизированных производств / Под ред. Б.Н.Малиновского. – К.: Технiка, 1986. – 160 с.