Стаття учня до проекту "Таємниці руху"
Зміст
Тема проекту: Таємниці руху
Наша команда
"Математики": Софія Іванова, Микола Петренко, Ліля Синиця
Тема дослідження: Поворот
Проблема дослідження:
проектувальникам лінії зв'язку потрібно з'єднати пункти А, В і С. Як побудувати цю лінію, щоб витратити найменшу кількість кабелю?
Гіпотеза дослідження
Ми перефразували задачу наступним чином: потрібно всі три точки з'єднати відрізками так, щоб сума довжин всіх відрізків лінії зв’язку була найменшою.
Випадок 1. Якщо точки А, В і С лежать на одній прямій, то, зрозуміло, мінімальною лінією зв’язку буде відрізок, який з’єднує крайні точки.
Випадок 2. Точки А, В і С не лежать на одній прямій. Софія припустила, що мінімальною лінією зв’язку буде АВ+ВС+АС. У Миколи та Лілі виникли сумніви.
Мета дослідження
Результати дослідження
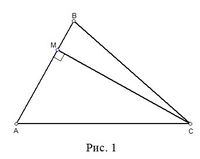
Ми розглянули найкоротшу відстань від точки С до АВ, тобто точку М, яка лежить на прямій АВ, причому СМ перпендикулярне АВ (рис.1). Тоді можна помітити, що АМ+ВМ+СМ<АВ+ВС+АС. Отже потрібно знайти таку точку М, щоб АМ+ВМ+СМ=min.
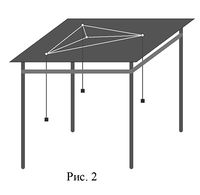
На допомогу нам прийшли фізики. На дерев’яному столі намалювали трикутник, просвердлили у вершинах дірочки, протягнули мотузки та зв’язали їх в одній точці над столом (рис. 2).
Прив’яжемо до вільних кінців гирьки однакової маси та відпустимо. Гирьки будуть намагатися опуститися якомога нижче (точніше, мінімізувати потенційну енергію системи трьох ваг). У найнижчому положенні сили врівноважать одна одну у внутрішній точці М трикутника або притягнуть точку М до однієї з вершин і будуть тягнути її «під стіл». Яка ж умова рівноваги у цьому випадку? Сума векторів однакової довжини дорівнює нулю тоді і тільки тоді, коли вони утворюють один з одним кути величиною 120°. Точку М у цьому випадку називають точкою Торрічеллі. Фізика підказала нам ідею розв’язування цієї задачі, але щоб знайти точку М, повернемося до геометрії. Розглянемо трикутник АВС. Нехай М – шукана точка, тоді АМ+ВМ+СМ=min. 1). Застосувавши поворот навколо точки А, отримаємо: точка В переходить в точку В1, точка М переходить в точку М1. Тоді АВ = АВ1, АМ = АМ1 = ММ1. Таким чином відрізок ВМ переходить у відрізок В1М1, тоді ВМ = В1М1. 2). Розглянемо АМ + ВМ + СМ = ММ1 + В1М1 +СМ ≥ В1С, тоді точки М і М1 належать відрізку В1С. 3). Застосувавши поворот навколо точки С, отримаємо: точка В переходить в точку В2, точка М переходить в точку М2. Тоді відрізок ВМ переходить у відрізок В2М2, тому ВМ = В2М2.
Висновки
Корисні ресурси
Сторінка проекту Назва проекту
Кіровоградський державний педагогічний університет імені Володимира Винниченка