Методи побудови опорного плану ТЗ.
Зміст
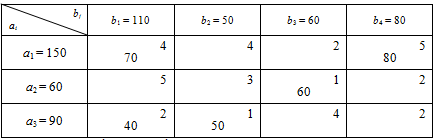
Метод північно-західного кута
Ідея методу північно-західного кута полягає в тому, що заповнення таблиці починають, не враховуючи вартостей перевезень, з лівого верхнього (північно-західного) кута. У клітину записують менше з двох чисел Неможливо розібрати вираз (невідома помилка): a_{i}
та Неможливо розібрати вираз (невідома помилка): b_{i}
. Далі переходять до наступної клітини в цьому ж рядку або у стовпчику і заповнюють її, і т. д. Закінчують заповнення таблиці у правій нижній клітинці. У такий спосіб значення поставок будуть розташовані по діагоналі таблиці.
Метод північно-західного кута є найпростішим, однак і найменш ефективним. Визначимо загальну вартість перевезень згідно з початковим опорним планом.
Неможливо розібрати вираз (невідома помилка): F=110\times 4+40\times 4+10\times 3+50\times 1+10\times 4+80\times 2=880
(ум. од.).
Теорема
Опорний план транспортної задачі, знайдений методом північно-західного кута, завжди ациклічний.
Метод мінімальної вартості
Ідея методу мінімальної вартості полягає в тому, що на кожному кроці заповнюють клітинку таблиці, яка має найменшу вартість перевезення одиниці продукції. Такі дії повторюють доти, доки не буде розподілено всю продукцію між постачальниками та споживачами.
В результаті таких міркувань отримали початковий опорний план, загальна вартість перевезень для якого становить: Неможливо розібрати вираз (невідома помилка): F=70\times 4+80\times 5+60\times 1+50\times 1+40\times 2=870
Значення цільової функції менше за попередній варіант, значить цей план ближчий до оптимального.
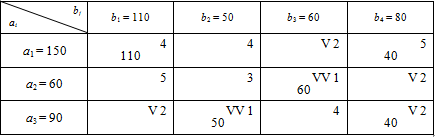
Метод подвійної переваги
Якщо розмірність задачі досить велика, то перебір за методом мінімальної вартості ускладнюється. В такому разі спростити пошук клітин з найменшими вартостями можна, застосовуючи метод подвійної переваги.
Згідно з процедурою цього методу перед початком заповнення таблиці необхідно позначити будь-якими символами клітинки, які містять найменшу вартість у рядках, а потім — у стовпчиках. Таблицю починають заповнювати з клітинок, позначених двічі (які містять вартості, що є мінімальними і в рядку, і в стовпчику). Далі заповнюють клітинки, позначені один раз (що містять мінімальні вартості або в рядку, або в стовпчику), а вже потім — за методом мінімальної вартості.
Неможливо розібрати вираз (невідома помилка): F=110\times 4+40\times 5+60\times 1+50\times 1+40\times 2=830
Застосування для побудови опорного плану даного методу уможливлює отримання найменшого у зіставленні з розглянутими вище значення цільової функції. Отже, такий план є найближчим до оптимального.
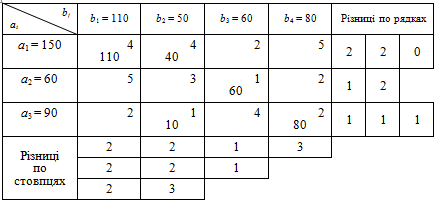
Метод апроксимації Фогеля
За цим методом на кожному кроці визначають різницю між двома найменшими вартостями в кожному рядку і стовпчику транспортної таблиці. Ці різниці записують у спеціально відведених місцях таблиці — знизу та справа у кілька рядків та стовпчиків, що відповідають крокам заповнення таблиці. Зпоміж усіх різниць вибирають найбільшу і у відповідному рядку чи стовпчику заповнюють клітинку з найменшою вартістю. Якщо ж однакових найбільших різниць кілька, то вибирають будь-який відповідний рядок або стовпчик. Коли залишається незаповненим лише один рядок або стовпчик, то обчислення різниць припиняють, а таблицю продовжують заповнювати за методом мінімальної вартості. Даний метод побудови опорного плану враховує не лише маршрути з мінімальними витратами перевезень продукції, але й співвідношення витрат у рядку чи стовпчику, тобто розраховується наскільки, може збільшитися вартість постачання на наступних кроках процедури, якщо не здійснити на поточному кроці постачання в клітину з мінімальною вартістю. Метод апроксимації Фогеля дає змогу особливо для задач великих розмірностей скласти найкращий опорний план.
У таблиці навпроти кожного рядка і стовпчика записані величини, які знайдені як різниці між мінімальним значенням вартості та наступним за ним по рівню. Максимальне значення такої різниці на першому кроці відповідає четвертому стовпчику і означає, що у разі, коли не буде задоволена потреба четвертого споживача перевезенням продукції від третього постачальника за ціною 2 ум. од. за одиницю, то на наступних кроках вартість перевезення може бути на 3 ум. од. більшою. Тобто інакше може статися, що потребу четвертого споживача необхідно буде задовольняти перевезенням продукції від першого постачальника, що призведе до збільшення вартості цього перевезення в 2,5 рази. Водночас для всіх інших споживачів та постачальників такі різниці є меншими. Отже, найдоцільніше на першому кроці заповнити клітину А3В4. Після цього потреби В4 повністю задоволені, і всі клітини четвертого стовпчика виключаються з наступного розрахунку різниць по рядках і стовпцях.
На другому кроці максимальна різниця дорівнює 2 і відповідає першому і другому рядкам та першому і другому стовпчикам, тому можна заповнювати будь-яку їх клітину з мінімальною вартістю, наприклад, А2В3. Після цього з розгляду виключаються одразу всі клітини другого рядка та третього стовпця, оскільки потреби третього споживача повністю задоволені, а запаси другого постачальника вичерпані. Останній розрахунок різниць (найбільше значення 3 відповідає другому стовпчику) свідчить про доцільність введення поставки від третього постачальника до другого споживача. Решту клітин заповнимо методом мінімальної вартості та визначимо загальну вартість перевезень:
Неможливо розібрати вираз (невідома помилка): F=110\times 4+40\times 4+60\times 1+10\times 1+80\times 2=830
Результат збігся із значенням цільової функції для опорного плану, що складений за попереднім методом. Ефективність методу апроксимації Фогеля, як вже згадувалось, є очевидною для задач більшої розмірності.
Зазначимо, що ефективність наведених методів можна оцінювати лише в середньому, оскільки можлива ситуація, що методом мінімальної вартості отримано опорний план транспортної задачі кращий, ніж методом подвійної переваги.