Стаття проекту "Урок майбутнього!" Коровкіна Ольга

Навчальний предмет

Геометрія

Вік учнів, клас

16-18 років. 11 клас.

Тема уроку

Правильна піраміда. Формула для обчислення площі бічної поверхні піраміди.

Тип уроку

Вибрати один із списку:

• Комбінований

Мета уроку

Навчальна мета :

• повторити, привести в систему й розширити відомості про піраміди;
• формувати вміння знаходити невідомі елементи, площу поверхні піраміди;

Розвивальна мета:

• розвивати просторову уяву, культуру математичного мовлення, пізнавального інтересу через творчу активність;
• розвити емоційно – сприятливе відношення до вивчення геометрії;

Виховна мета : виховувати вольові якості, цілеспрямованість;

Хід уроку

1. Повідомлення теми, мети і завдань уроку, мотивація учіння школярів.

Привітання з учнями. Налаштування учнів на роботу.
У когось слово піраміда асоціюється з єгипетськими пірамідами, але монументальні споруди створені руками людини зустрічаються і в Центральній Америці, на острові Тенериф, на фоні Гімалайського хребта виділяється пірамідальне утворення, створене природою. Пірамідальна форма широко використовується в архітектурі.

Правильні многокутники можуть бути як бічними гранями піраміди так і її основою. А піраміда в основі якої лежить правильний многокутник називається правильною пірамідою. Тому тема нашого сьогоднішнього уроку: «Правильна піраміда. Формула для обчислення площі бічної поверхні піраміди».

[Блог учителя "Цікава геометрія"

2. Перевірка домашнього завдання, повторення раніше вивче­ного матеріалу.

Перед уроком учні консультанти перевіряють наявність та правильність виконання домашнього завдання і повідомляють про роботу на уроці.

3. Актуалізація і корекція опорних знань, навичок і вмінь; повідомлення теми, цілей і завдань уроку; актуалізація мотивації учіння учнів.

Араби склали приказку: «Все на світі боїться часу, але час боїться пірамід». Отже, ми відправляємося у подорож цікавим світом математики, де існують загадкові піраміди.

Перед класом повідомлення читає учень, перевдягнений у давньогрецького математика Піфагора.

У німій далечі застигли піраміди фараонів, величні, як вічність, мовчазні, немов смерть.

Все на світі боїться часу, а час боїться пірамід. Вони підносяться серед гарячих пісків Лівійської пустелі і тягнуться на десятки кілометрів; від сучасного Каїрадо Фаюмського каналу. До нашого часу збереглося близько сімдесяти цих величних споруд. Колись їх було більше, але деякі зруйнував всевладний час, інші засипав пісок, що насунувся з пустелі.

Найвідоміші піраміди: Хеопса, Хефрена, Мікеріна. Найбільша з них – велика піраміда Хеопса, збудована в XXVI ст. до н. е. Висота її 147 метрів, а площа основи близько 55 000 квадратних метрів. Згідно з легендами, піраміда служила фараонам тією драбиною, якою вони сходили на небо. Із семи відомих історії чудес світу, що не кажіть, а піраміди залишаються дивом № 1.

Уже давно висохли і розсипалися в прах висячі сади Семіраміди, та від Вавилона, який вони прикрашали, лишилися одні уламки. Гола площина з потрощеним камінням видніє нині на місці, де стояла колись оселя богині зміїв – храм Артеміди в Ефесі. Тут, на Малоазіатському узбережжі, де гомоніла Гомерові Троя, було ще одне диво – пам'ятник великому коханню – мавзолей у Галікарнасі. Землетрус повалив на землю Колоса – величну статую променистого бога Геліоса, що зустрічав усі кораблі біля гавані на острові Родосі Безслідно зникла перевезена з Олімпії до Константинополя статуя Зевса, створена геніальним Фідієм. І підвалин найвищого в світі Александрійського маяка вже не знайти. Лише тут, де Ніл братається з морем, на плато Піза стоять руді, як гарячий пісок Сахари, гранчасті гостроверхі пагорби. Воістину, як мовить арабське прислів'я, все боїться часу, а час боїться пірамід».

Два архітектурних дива на Полтавщині, дві з трьох українських пірамід-усипальниць як віддзеркалення ставлення в Україні до пам’яток архітектури. Як два кінці однієї палиці.

Піраміду у Березовій Рудці (Пирятинський район) збудував зять Петра Столипіна, колишній посол Російської Імперії у Єгипті Ігнатій Закревський у 1898 – 1899 рр. Тому по поверненню додому вирішив спорудити каплицю над могилами батьків у вигляді піраміди (висота – 9 м).

Іншу полтавську піраміду у селі Комендантівка (Кобеляцький район) спорудили двома десятками років раніше. Офіцер російського флоту Олександр Білевич (Белевич), побувавши на початку 1860 – х років у Єгипті, також був вражений величчю пірамід у Гізі, та вирішив збудувати щось подібне у себе.

Тож і ми, розглядаючи піраміду як геометричну фігуру, не забуваймо, що за нею стоїть велич віків та могутність сьогодення.

4. Вивчення нового матеріалу (вступні, мотиваційні та пізнавальні вправи).

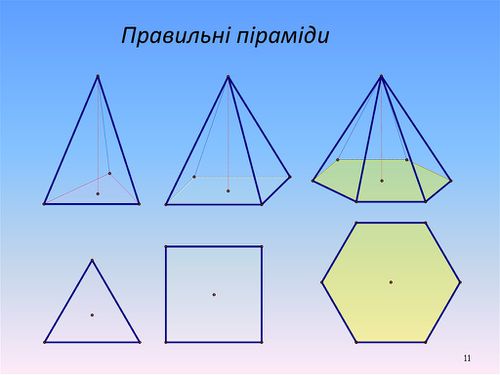
Перед початком викладу матеріалу потрібно звернути увагу учнів на те, що на уроці буде розглядатись правильна піраміда, в основі якої лежи рівносторонній трикутник. Всі означення справджуються і для правильних пірамід в основі яких лежать правильні n-кутники. Викладаючи новий матеріал доцільно проводити не лекцію, а давати учням можливість висловити свою думку, а потім вчитель формулює означення.

Означення

Піраміда називається правильною, якщо її основою є правильний багатокутник (ABC), а його центр (т. О) збігається з основою висоти піраміди. Усі бічні ребра правильної піраміди рівні (FA=FB=FC) та всі ребра при основі рівні (AB=BC=AC). Усі бічні грані правильної піраміди – рівні рівнобедрені трикутники.

Означення

Висоту бічної грані (FD) правильної піраміди, проведену з її вершини, називають апофемою піраміди.

Зверніть увагу!

• Неправильні піраміди апофеми не мають.
• Піраміда у якої всі бічні грані є правильні трикутники називається тетраедром.
• Бічна поверхня піраміди складається з усіх бічних граней.

Теорема
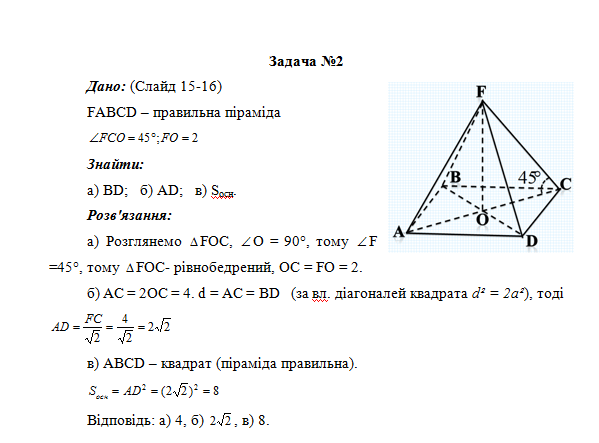
Площа бічної поверхні правильної піраміди дорівнює добутку півпериметра її основи на апофему піраміди.
S(б.)=1/2*Pl
Площа поверхні піраміди дорівнює сумі площі її бічної поверхні та площі основи.
S(п)= S(б)+ S(о)


Практична робота У кожної групи учнів на столі стоять правильні піраміди. Їм пропонується знайти площу бічної поверхні піраміди, попередньо зробивши потрібні виміри.

Робота в групах
Кожна група учнів виконує з підручника одну дужку № 802 (а – г). Учитель контролює розв’язання. Після виконання вправ учні на дошці будують малюнок, представляють свої розв’язки.
№ 802
Знайдіть площу поверхні правильної чотирикутної піраміди, якщо:
І група
а. сторона основи дорівнює а, а двогранний кут при ребрі основи α;
ІІ група
б. висота піраміди дорівнює h, а бічне ребро утворює з площиною основи кут 45°;
ІІІ група
в. бічне ребро дорівнює b та утворює з площиною основи кут β;
IV група
г. відстань від основи висоти до бічної грані дорівнює d, а двогранний кут при ребрі основи α.

5. Підсумки уроку.

А зараз давайте підсумуємо те, що ми вивчили і виконаємо тренувальні вправи тестового змісту.
Метод «Чотири ЩО?»

• Що ви дізналися, навчилися на уроці?
• Що сподобалося найбільше?
• Що було найскладнішим?
• Що треба ще вивчити?

6. Повідомлення домашнього завдання.

Опрацювати Розділ 2: § 22 (ст. 152 – 154)
Учні, які ще не досить впевнені в своїх знаннях виконують № 803 (а – б) та № 805
Опрацювати доведення теореми про площу бічної поверхні правильної піраміди самостійно (ст. 153)
№ 803 (г) та № 830

Методичні та дидактичні матеріали

1. Блог учителя "Цікава геометрія"
2. Cтінгазета
3. Тест для перевірки знань
4. Ментальні карти
5. Інтерактивна гра
6. Запрошення на гурток
7. Електронний журнал (https://docs.google.com/spreadsheets/d/11XGcoQxyom82UoYVCuPbiV_VjfFvMrm5mdydW1K3NQs/edit?usp=sharing)

Інформаційні ресурси

Друковані джерела

1. Апостолова Г.В. Геометрія. 11 клас. Академічний і профільний рівень
2. Бевз Г.П., Бевз В.Г., Владімірова Н.Г., Владіміров В.М. Геометрія. 11 клас. Академічний та профільний рівень
3. Бевз Г.П., Бевз В.Г., Владімірова Н.Г. Геометрія 10-11

Відеоматеріали

1. чотирикутна піраміда
2. Як зробити правильну піраміду з паперу

Електронні ресурси

1. Правильна піраміда
2. Українські піраміди
3. Калькулятор площі поверхні піраміди

---

Автор статті

Студентка фізико-математичного факультету 6 курсу, спеціальність "МІ17М" Коровкіна Ольга

Центральноукраїнський державний педагогічний університет імені Володимира Винниченка