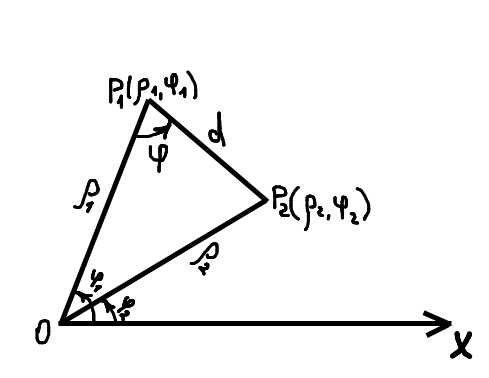
Теореми додавання для циліндричних функцій.

Нехай задані точки: Неможливо розібрати вираз (невідома помилка): P_1(\rho_1,\varphi_1)

, Неможливо розібрати вираз (невідома помилка): P_2(\rho_2,\varphi_2)
, 0(0,0) в полярній системі координат.

Нехай Неможливо розібрати вираз (невідома помилка): \rho_1>\rho_1

 , Неможливо розібрати вираз (невідома помилка): |{P_1P_2}|=d
, Неможливо розібрати вираз (невідома помилка): 0\leq|\varphi|<\frac{\pi}{2}

В таких позначеннях виконується співвідношення:

Неможливо розібрати вираз (невідома помилка): {d^2}={\rho_1}^2+{\rho_2}^2-2{\rho_1}{\rho_2}cos(\varphi_1-\varphi_2)

Неможливо розібрати вираз (невідома помилка): e^{(2i\varphi)}=\frac{\rho_1-\rho_2e^{-i(\varphi_1-\varphi_2)}}{\rho_1-\rho_2e^{i(\varphi_1-\varphi_2)}}

Для будь-якої циліндричної функції Неможливо розібрати вираз (невідома помилка): {Z_m(z)}

справедлива теорема додавання:

Неможливо розібрати вираз (невідома помилка): {Z_m({\alpha}{d})}e^{{i}{m}{\varphi}}=\sum^{+\infty}_{k=-\infty}{Z_{m+k}}({\alpha}{\rho_1}){J_k}({\alpha}{\rho_2})e^{ik(\varphi_1-\varphi_2)}

  , де Неможливо розібрати вираз (невідома помилка): {\alpha}=const

Значення циліндричної функції в будь-якій точці можна записати у вигляді ряду по функціям Бесселя, якщо відомі параметри у одній фіксованій точці Неможливо розібрати вираз (невідома помилка): {P_1}

Частковий випадок:

Неможливо розібрати вираз (невідома помилка): \varphi_1-\varphi_2={\pi}

Неможливо розібрати вираз (невідома помилка): {Z_m({\alpha}(\rho_1+\rho_2))}=\sum^{+\infty}_{k=-\infty}{Z_k({\alpha}{\rho_1})}{J_{m-k}({\alpha}{\rho_2})}