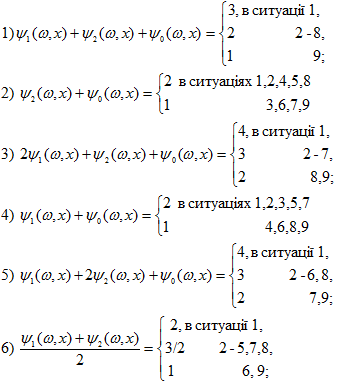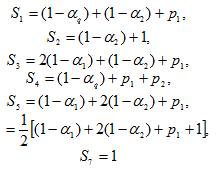Відмінності між версіями «Одноетапна Р-модель з імовірнісними обмеженнями. Алгоритм побудови розв’язувального правила. Приклад.»
| Рядок 1: | Рядок 1: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Формально задача записується у наступному вигляді: | Формально задача записується у наступному вигляді: | ||
| Рядок 11: | Рядок 5: | ||
<math> P{x(\omega)\in G_i(\omega)}\ge\alpha_i,i=1,2,...,m</math> (4.2) | <math> P{x(\omega)\in G_i(\omega)}\ge\alpha_i,i=1,2,...,m</math> (4.2) | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
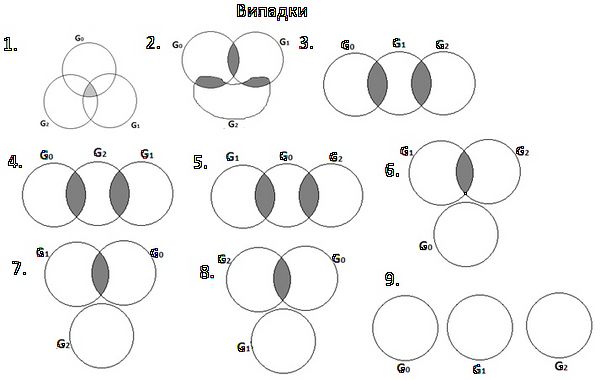
Можна вказати наступні дев'ять попарно несумісних ситуацій взаємного розміщення множин <math> G_i, i=0,1,2,</math> які показують всі можливі випадки. | Можна вказати наступні дев'ять попарно несумісних ситуацій взаємного розміщення множин <math> G_i, i=0,1,2,</math> які показують всі можливі випадки. | ||
| Рядок 80: | Рядок 51: | ||
<math> u_i^j</math> - умовна ймовірність події <math> x \in U^j</math> за умови, що має місце ''і''-та ситуація взаємного розміщення множин <math> G_k</math>. | <math> u_i^j</math> - умовна ймовірність події <math> x \in U^j</math> за умови, що має місце ''і''-та ситуація взаємного розміщення множин <math> G_k</math>. | ||
| + | |||
| + | Мають місце співвідношення: <math> \sum^{7}_{j=1} u_i^j =1, i=1,...,9 </math>. Задача (4.1)-(4.2) еквівалентна наступній задачі ЛП: | ||
| + | |||
| + | <math> f(u)=\sum^{9}_{i=1} p_i(u_i^1+u_i^2+u_i^3+u_i^5) \rightarrow sup? i=1,...,9 </math>. (4.3) | ||
| + | |||
| + | <math> f(u)=\sum^{9}_{i=1} p_i(u_i^1+u_i^2+u_i^3+u_i^5) \rightarrow sup, </math> (4.3) | ||
| + | |||
| + | <math> \sum^{9}_{i=1} p_i(u_i^1+u_i^2+u_i^4+u_i^6) \geqslant \alpha_1 </math> (4.4) | ||
| + | |||
| + | <math> \sum^{9}_{i=1} p_i(u_i^1+u_i^3+u_i^4+u_i^7) \geqslant \alpha_2 </math> (4.5) | ||
| + | |||
| + | <math> \sum^{9}_{i=1}u_i^j =1 , i=1,...9,</math> (4.6) | ||
| + | |||
| + | <math> u_i^j \geqslant 0 , i=1,...9, j=1,...,7</math> . (4.7) | ||
| + | |||
| + | Деякі зі змінних <math> u_i^j </math> для окремих ситуацій рівні 0. Маємо: | ||
| + | |||
| + | <math> \begin{cases} u_i^1=0, i=2,...,9, \\ u_i^2=0, i=4,6,8,9, \\ u_i^3=0, i=3,6,7,9,\\u_i^4=0, i=5,7,8,9 \end{cases} </math> (4.8) | ||
| + | |||
| + | Побудуємо двоїсту задачу до задачі (4.3)-(4.8): | ||
| + | |||
| + | <math> g(\lambda)=-\alpha_1 \lambda_1 - \alpha_2\lambda_2+ \sum^{9}_{i=1}\lambda_{i+2} \rightarrow inf </math> (4.9) | ||
| + | |||
| + | <math> \begin{cases} \lambda_{i+2}\geqslant\begin{cases} p_i(1+\lambda_1+\lambda_2), i=1,\\ p_i(1+\lambda_1+\lambda_2)-\lambda_i^1, i=2,...,9,\end{cases}\\ | ||
| + | \lambda_{i+2}\geqslant\begin{cases} p_i(1+\lambda_1), i=1,2,3,5,7,\\ p_i(1+\lambda_2)+\lambda_i^2, i=1,2,3,5,7,\end{cases}\\ | ||
| + | \lambda_{i+2}\geqslant\begin{cases} p_i(1+\lambda_2), i=1,2,3,5,7,\\ p_i(1+\lambda_2)-\lambda_i^3, i=3,6,7,9,\end{cases}\\ | ||
| + | \lambda_{i+2}\geqslant\begin{cases} p_i(\lambda_1+\lambda_2), i=1,2,3,4,6,\\ p_i(\lambda_1+\lambda_2)-\lambda_i^4, i=5,7,8,9,\end{cases}\\ | ||
| + | \lambda_{i+2}\geqslant p_i, i=1,...,9,\\ | ||
| + | \lambda_{i+2}\geqslant p_i\lambda_1, i=1,...,9,\\ | ||
| + | \lambda_{i+2}\geqslant p_i\lambda_2, i=1,...,9, | ||
| + | \end{cases} | ||
| + | </math> (4.10) | ||
| + | |||
| + | <math> \lambda_1 \geqslant 0,\lambda_2 \geqslant 0 </math> (4.11) | ||
| + | |||
| + | |||
| + | Тут двоїсті змінні <math> \lambda_1 ,\lambda_2 </math> відповідають обмеженням (4.4) та (4.5) прямої задачі, змінні <math> \lambda_{i+2} (i=1,...,9) </math> відповідають умовам (4.6), а <math> \lambda_i^j(i=1,...,9, j=1,2,3,4)</math> - умовам (4.8). | ||
| + | |||
| + | Позначимо через <math> \phi_i^k (\lambda_1, \lambda_2), (i=1,...,9; k=1,...7)</math> лінійні функції змінних <math> \lambda_1 ,\lambda_2 </math> які входять у праві частини умов (4.10), а через </math> лінійні функції змінних <math> K(i)</math> - множину індексів, для яких відповідні умови із співвідношень (4.10) не містять змінних <math> \lambda_i^k</math>. Тоді нерівності (4.10) можна переписати у вигляді: | ||
| + | |||
| + | <math> \lambda_{i+2}\geqslant \begin{cases}\phi_i^k, k\in K(i), \\ \phi_i^k - \lambda_i^k, k\notin K(i). \end{cases} </math> (4.12) | ||
| + | |||
| + | Маємо наступні функції: | ||
| + | |||
| + | <math> \phi_i(\lambda_1,\lambda_2) = max_{k\in K(i)} {\phi_i^k (\lambda_1,\lambda_2)} </math> (4.13) | ||
| + | |||
| + | <math> \zeta_i(\lambda_1,\lambda_2, \lambda_i^k) = max_{k \in K(i)} {\phi_i^k (\lambda_1,\lambda_2) - \lambda_i^k } </math> (4.14) | ||
| + | |||
| + | Тоді: | ||
| + | |||
| + | <math> \lambda_i+2 \geqslant max {\phi_i, \zeta_i} </math> (4.15) | ||
| + | |||
| + | '''Лема 4.1.''' На оптимальному плані задачі (4.9)-(4.11) мають місце рівності | ||
| + | |||
| + | <math> \lambda_i+2 = phi_i(\lambda_1,\lambda_2), (i=1,…9) </math> (4.16) | ||
| + | |||
| + | '''Теорема 4.2.''' Якщо умови задачі (4.1)-(4.2) сумісні, то sup''f(x)''за умов (4.4.)-(4.7) рівний найменшому з семи чисел: | ||
| + | |||
| + | <math> S_1=(1-\alpha_1)+p_1-p_9, </math> | ||
| + | |||
| + | <math> S_2=(1-\alpha_2)+1-p_3-p_6-p_7-p_9, </math> | ||
| + | |||
| + | <math> S_3=2(1-\alpha_1)+(1-\alpha_2)+p_1-p_8-p_9, </math> | ||
| + | |||
| + | <math> S_4=(1-\alpha_1)+1-p_4-p_6-p_8-p_9, </math> | ||
| + | |||
| + | <math> S_5=(1-\alpha_1)+2(1-\alpha_2)+p_1-p_7-p_9, </math> | ||
| + | |||
| + | <math> S_6={1/2}[(1-\alpha_1)+(1-\alpha_2)+1-p_1-p_6-p_9], </math> | ||
| + | |||
| + | <math> S_7=1 </math> | ||
| + | [[Файл:YMDO2.jpg|600px|thumb|right]] | ||
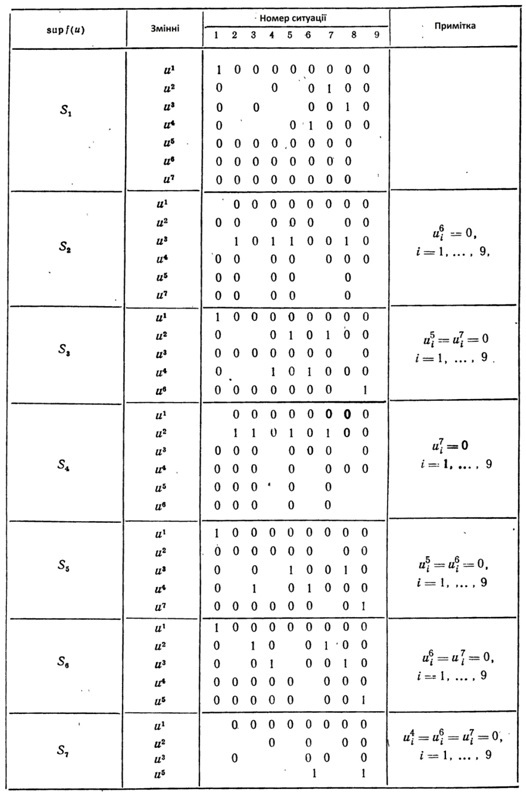
| + | Умова <math> f(u)-S_k </math> разом з обмеженнями (4.10), (4.11) висікає множину оптимальних планів задачі. Для кожного набору параметрів умов задачі <math> (\alpha_1,\alpha_2,p_i) </math> оптимальні значення <math> u_i^j </math> належать одній з семи множин. Використовуючи другу теорему двоїстості лінійного програмування, можна виділити серед компонент розв'язку "вільні" та "закріплені". Таким чином отримаємо можливість, не розв'язуючи задачі, визначити оптимальні значення частини змінних , незалежно від реалізації випадкових параметрів умов задачі. Маючи на увазі, крім цього, співвідношення (4.8), отримаємо таблицю 4.1. | ||
| + | |||
| + | Використовуючи таблицю 4.1. можна спростити рівняння і нерівності, які визначають сім (по числу Sk) можливих багатогранних множин оптимальних планів задачі (4.3)-(4.7). Маємо: | ||
| + | |||
| + | <math> \begin{cases} p_2(u_2^2+u_2^4)+ p_4 u_4^4+ p_5 u_5^2+ p_9 u_9^6 =\alpha_1 - p_1 - p_3 - p_6 - p_7,\\ p_2(u_2^2+u_2^4)+ p_4 u_3^4 + p_5 u_5^2+ p_9 u_9^6 =\alpha_2 - p_1 - p_4 - p_6 - p_8,\\ u_2^2 +u_2^3+u_2^4=1, u_3^2+u_3^4 =1, \\ u_4^3 +u_4^4=1, u_5^2+u_5^3 =1,\\ u_9^2 +u_9^6+u_9^7=1, u_i^j \geqslant 0 | ||
| + | \end{cases}</math> (4.19) | ||
| + | |||
| + | <math> \begin{cases} p_3(u_3^2+u_3^5)+ p_6 u_6^5+ p_7( u_7^2+u_7^5)+p_9 u_9^5 =1-\alpha_2,\\ p_2u_1^1+ p_3 (u_3^2 u_3^4)+ p_6 u_6^4 + p_7 u_7^2=\alpha_1 \\ u_1^1 +u_1^3=1, u_3^2+u_3^4 + u_3^5+u_3^7=1, \\ u_5^4 +u_6^5+u_6^7=1, u_7^2+u_7^5+u_7^7 =1,\\ u_5^9 +u_9^7=1, u_i^j \geqslant 0 | ||
| + | \end{cases}</math> (4.20) | ||
| + | |||
| + | [[Файл:YMDO3.png|600px]] | ||
| + | |||
| + | Таким чином, маємо: | ||
| + | |||
| + | '''Наслідок 4.2.''' Множина оптимальних планів задачі (4.3)-(4.7) визначається таблицею 4.1. та однією з систем (4.19)-(4.25) (в залежності від значень α2, α1, та pi). | ||
| + | |||
| + | '''Теорема 4.3.''' Якщо задача (4.1)-(4.2) сумісна, то існує ф-я <math> x*(\omega) </math> яка є розв'язком задачі. При цьому, якщо верхня грань цільового функціонала <math> S(\alpha_1,\alpha_2)</math> рівна k-му числу системи, яка визначається теоремою 4.2., тоді розв'язки задачі і тільки вони задовольняють умовам (4.2) та k-му рівнянню наступної системи: | ||
| + | |||
| + | [[Файл:Ymdo4.png|400px]] | ||
| + | |||
| + | '''Приклад.''' Розглянемо наступну задачу стохастичного програмування: | ||
| + | |||
| + | <math> P\{c(\omega) x(\omega) \geqslant L{\omega) } \rightarrow sup,</math> (4.26) | ||
| + | |||
| + | <math> \begin{cases} P\{A(\omega) x(\omega) \leqslant b{\omega)} \geqslant \alpha_1,\\ P{x(\omega) \geqslant 0} \geqslant \alpha_2\end{cases}</math> (4.27) | ||
| + | |||
| + | Припускається, що вип. вел. <math> L(\omega)</math> , всі компоненти вип. векторів <math> c(\omega) i b(\omega)</math> та елементи вип. матриці <math> A(\omega)</math> невід'ємні майже при всіх <math> \omega</math> Тоді з ймовірністю 1 множина <math> G_1 \cap G_2 \ne \varnothing </math>. | ||
| + | |||
| + | Нехай крім цього <math>P \{ c(\omega) =0. </math>. Це означає, що <math> G_1 \cap G_2 \ne \varnothing </math> з ймовірністю 1. | ||
| + | |||
| + | Таким чином, з 9 ситуацій з додатною ймовірністю з'язляються тільки 3: 1, 2, 4. Тобто: <math> p_3=p_5=p_6=p_7=p_8=p_9=0 </math> (4.28) | ||
| + | |||
| + | <math> p_1=p_2=p_4=1 </math> (4.29) | ||
| + | |||
| + | Випишемо, враховуючи (4.28)-(4.29), можливі значення верхньої грані цільової функції задачі (4.1)-(4.2): | ||
| + | |||
| + | [[Файл:3ytfe.png]] | ||
| + | |||
| + | Очевидно, що <math> S_2\geqslant S_1, S_5 \geqslant S_1</math>. Крім цього, якщо <math> S_1 < 1</math> то <math> S_6 , S_1</math>. Якщо ж <math> S_1 \geqslant 1</math> то <math> S_6 \geqslant 1</math>.Отже, <math> S_2 \geqslant S_7</math>. Тобто оптимальне значення цільової функції задачі (4.1)-(4.2) може дорівнювати одному з 3-х чисел <math> S_1, S_4, S_7</math>. Розглянемо ці випадки послідовно: | ||
| + | |||
| + | А) <math> S(\alpha_1,\alpha_2)=S_1= (1-\alpha_1)+(1-\alpha_2)+p_1</math> | ||
| + | |||
| + | [[Файл:4345f.png]] | ||
Версія за 21:03, 11 квітня 2013
Формально задача записується у наступному вигляді:
Неможливо розібрати вираз (невідома помилка): P{x(\omega)\in G_0(\omega)}\rightarrow sup,
(4.1)
Неможливо розібрати вираз (невідома помилка): P{x(\omega)\in G_i(\omega)}\ge\alpha_i,i=1,2,...,m
(4.2)
Можна вказати наступні дев'ять попарно несумісних ситуацій взаємного розміщення множин Неможливо розібрати вираз (невідома помилка): G_i, i=0,1,2,
які показують всі можливі випадки.
1. Неможливо розібрати вираз (невідома помилка): G_1\cap G_2 \cap G_0 \ne \varnothing
2. Неможливо розібрати вираз (невідома помилка): G_1\cap G_2 \cap G_0 = \varnothing, G_1\cap G_2 = \varnothing, G_1\cap G_0 \ne \varnothing
3. Неможливо розібрати вираз (невідома помилка): G_1\cap G_2 \cap G_0 = \varnothing, G_1\cap G_2 \ne \varnothing, G_1\cap G_0 \ne \varnothing
4. Неможливо розібрати вираз (невідома помилка): G_1\cap G_2 \ne \varnothing, G_1\cap G_0 = \varnothing, G_2\cap G_0 \ne \varnothing
5. Неможливо розібрати вираз (невідома помилка): G_1\cap G_2 = \varnothing, G_1\cap G_0 \ne \varnothing, G_2\cap G_0 \ne \varnothing
6. Неможливо розібрати вираз (невідома помилка): G_1\cap G_2 = \varnothing, G_1\cap G_0 = \varnothing, G_2\cap G_0 = \varnothing
7. Неможливо розібрати вираз (невідома помилка): G_1\cap G_2 = \varnothing, G_1\cap G_0 \ne \varnothing, G_2\cap G_0 = \varnothing
8. Неможливо розібрати вираз (невідома помилка): G_1\cap G_2 = \varnothing, G_1\cap G_0 = \varnothing, G_2\cap G_0 \ne \varnothing
9. Неможливо розібрати вираз (невідома помилка): G_1\cap G_2 = G_1\cap G_0 = G_2\cap G_0 = \varnothing
Нехай Неможливо розібрати вираз (невідома помилка): \Omega_i
‒ множина тих Неможливо розібрати вираз (невідома помилка): \omega \in \Omega при яких реалізується і-та ситуація і Неможливо розібрати вираз (невідома помилка): p_i=P\Omega_i, i=1,...,9.
Розчленуємо множину Неможливо розібрати вираз (невідома помилка): U=\bigcup\limits_{k=0}^2 G_k
на 7 підмножин, які попарно не перетинаються, наступним чином:
Неможливо розібрати вираз (невідома помилка): U^1=G_0 \cap G_1 \cap G_2 ,
Неможливо розібрати вираз (невідома помилка): U^2=(G_0 \cap G_1)\setminus G_0 \cap G_1\cap G_2 ,
Неможливо розібрати вираз (невідома помилка): U^3=(G_0 \cap G_2) \setminus G_0 \cap G_1\cap G_2 ,
Неможливо розібрати вираз (невідома помилка): U^4=(G_1 \cap G_2)\setminus G_0 \cap G_1\cap G_2 ,
Неможливо розібрати вираз (невідома помилка): U^5=G_0\setminus [(G_0\cap G_1)\cup (G_0 \cap G_2)] ,
Неможливо розібрати вираз (невідома помилка): U^6=G_1 \setminus [(G_0\cap G_1)\cup (G_1 \cap G_2)] ,
Неможливо розібрати вираз (невідома помилка): U^7=G_2 \setminus [(G_0\cap G_2)\cup (G_1 \cap G_2)] ,
Очевидно, що Неможливо розібрати вираз (невідома помилка): U=\bigcup\limits_{j=0}^7 U^j; U^i \cap U^j = \varnothing
Введемо змінні Неможливо розібрати вираз (невідома помилка): u_i^j
Неможливо розібрати вираз (невідома помилка): u_i^j=P{x\in U^j | i}
Неможливо розібрати вираз (невідома помилка): u_i^j
- умовна ймовірність події Неможливо розібрати вираз (невідома помилка): x \in U^j за умови, що має місце і-та ситуація взаємного розміщення множин Неможливо розібрати вираз (невідома помилка): G_k
.
Мають місце співвідношення: Неможливо розібрати вираз (невідома помилка): \sum^{7}_{j=1} u_i^j =1, i=1,...,9 . Задача (4.1)-(4.2) еквівалентна наступній задачі ЛП:
Неможливо розібрати вираз (невідома помилка): f(u)=\sum^{9}_{i=1} p_i(u_i^1+u_i^2+u_i^3+u_i^5) \rightarrow sup? i=1,...,9 . (4.3)
Неможливо розібрати вираз (невідома помилка): f(u)=\sum^{9}_{i=1} p_i(u_i^1+u_i^2+u_i^3+u_i^5) \rightarrow sup,
(4.3)
Неможливо розібрати вираз (невідома помилка): \sum^{9}_{i=1} p_i(u_i^1+u_i^2+u_i^4+u_i^6) \geqslant \alpha_1
(4.4)
Неможливо розібрати вираз (невідома помилка): \sum^{9}_{i=1} p_i(u_i^1+u_i^3+u_i^4+u_i^7) \geqslant \alpha_2
(4.5)
Неможливо розібрати вираз (невідома помилка): \sum^{9}_{i=1}u_i^j =1 , i=1,...9,
(4.6)
Неможливо розібрати вираз (невідома помилка): u_i^j \geqslant 0 , i=1,...9, j=1,...,7
. (4.7)
Деякі зі змінних Неможливо розібрати вираз (невідома помилка): u_i^j
для окремих ситуацій рівні 0. Маємо:
Неможливо розібрати вираз (невідома помилка): \begin{cases} u_i^1=0, i=2,...,9, \\ u_i^2=0, i=4,6,8,9, \\ u_i^3=0, i=3,6,7,9,\\u_i^4=0, i=5,7,8,9 \end{cases}
(4.8)
Побудуємо двоїсту задачу до задачі (4.3)-(4.8):
Неможливо розібрати вираз (невідома помилка): g(\lambda)=-\alpha_1 \lambda_1 - \alpha_2\lambda_2+ \sum^{9}_{i=1}\lambda_{i+2} \rightarrow inf
(4.9)
Неможливо розібрати вираз (невідома помилка): \begin{cases} \lambda_{i+2}\geqslant\begin{cases} p_i(1+\lambda_1+\lambda_2), i=1,\\ p_i(1+\lambda_1+\lambda_2)-\lambda_i^1, i=2,...,9,\end{cases}\\ \lambda_{i+2}\geqslant\begin{cases} p_i(1+\lambda_1), i=1,2,3,5,7,\\ p_i(1+\lambda_2)+\lambda_i^2, i=1,2,3,5,7,\end{cases}\\ \lambda_{i+2}\geqslant\begin{cases} p_i(1+\lambda_2), i=1,2,3,5,7,\\ p_i(1+\lambda_2)-\lambda_i^3, i=3,6,7,9,\end{cases}\\ \lambda_{i+2}\geqslant\begin{cases} p_i(\lambda_1+\lambda_2), i=1,2,3,4,6,\\ p_i(\lambda_1+\lambda_2)-\lambda_i^4, i=5,7,8,9,\end{cases}\\ \lambda_{i+2}\geqslant p_i, i=1,...,9,\\ \lambda_{i+2}\geqslant p_i\lambda_1, i=1,...,9,\\ \lambda_{i+2}\geqslant p_i\lambda_2, i=1,...,9, \end{cases}
(4.10)
Неможливо розібрати вираз (невідома помилка): \lambda_1 \geqslant 0,\lambda_2 \geqslant 0
(4.11)
Тут двоїсті змінні Неможливо розібрати вираз (невідома помилка): \lambda_1 ,\lambda_2
відповідають обмеженням (4.4) та (4.5) прямої задачі, змінні Неможливо розібрати вираз (невідома помилка): \lambda_{i+2} (i=1,...,9)
відповідають умовам (4.6), а Неможливо розібрати вираз (невідома помилка): \lambda_i^j(i=1,...,9, j=1,2,3,4)
- умовам (4.8).
Позначимо через Неможливо розібрати вираз (невідома помилка): \phi_i^k (\lambda_1, \lambda_2), (i=1,...,9; k=1,...7)
лінійні функції змінних Неможливо розібрати вираз (невідома помилка): \lambda_1 ,\lambda_2 які входять у праві частини умов (4.10), а через </math> лінійні функції змінних Неможливо розібрати вираз (невідома помилка): K(i) - множину індексів, для яких відповідні умови із співвідношень (4.10) не містять змінних Неможливо розібрати вираз (невідома помилка): \lambda_i^k
. Тоді нерівності (4.10) можна переписати у вигляді:
Неможливо розібрати вираз (невідома помилка): \lambda_{i+2}\geqslant \begin{cases}\phi_i^k, k\in K(i), \\ \phi_i^k - \lambda_i^k, k\notin K(i). \end{cases}
(4.12)
Маємо наступні функції:
Неможливо розібрати вираз (невідома помилка): \phi_i(\lambda_1,\lambda_2) = max_{k\in K(i)} {\phi_i^k (\lambda_1,\lambda_2)}
(4.13)
Неможливо розібрати вираз (невідома помилка): \zeta_i(\lambda_1,\lambda_2, \lambda_i^k) = max_{k \in K(i)} {\phi_i^k (\lambda_1,\lambda_2) - \lambda_i^k }
(4.14)
Тоді:
Неможливо розібрати вираз (невідома помилка): \lambda_i+2 \geqslant max {\phi_i, \zeta_i}
(4.15)
Лема 4.1. На оптимальному плані задачі (4.9)-(4.11) мають місце рівності
Неможливо розібрати вираз (невідома помилка): \lambda_i+2 = phi_i(\lambda_1,\lambda_2), (i=1,…9)
(4.16)
Теорема 4.2. Якщо умови задачі (4.1)-(4.2) сумісні, то supf(x)за умов (4.4.)-(4.7) рівний найменшому з семи чисел:
Неможливо розібрати вираз (невідома помилка): S_1=(1-\alpha_1)+p_1-p_9,
Неможливо розібрати вираз (невідома помилка): S_2=(1-\alpha_2)+1-p_3-p_6-p_7-p_9,
Неможливо розібрати вираз (невідома помилка): S_3=2(1-\alpha_1)+(1-\alpha_2)+p_1-p_8-p_9,
Неможливо розібрати вираз (невідома помилка): S_4=(1-\alpha_1)+1-p_4-p_6-p_8-p_9,
Неможливо розібрати вираз (невідома помилка): S_5=(1-\alpha_1)+2(1-\alpha_2)+p_1-p_7-p_9,
Неможливо розібрати вираз (невідома помилка): S_6={1/2}[(1-\alpha_1)+(1-\alpha_2)+1-p_1-p_6-p_9],
Неможливо розібрати вираз (невідома помилка): S_7=1
Умова Неможливо розібрати вираз (невідома помилка): f(u)-S_k
разом з обмеженнями (4.10), (4.11) висікає множину оптимальних планів задачі. Для кожного набору параметрів умов задачі Неможливо розібрати вираз (невідома помилка): (\alpha_1,\alpha_2,p_i) оптимальні значення Неможливо розібрати вираз (невідома помилка): u_i^j належать одній з семи множин. Використовуючи другу теорему двоїстості лінійного програмування, можна виділити серед компонент розв'язку "вільні" та "закріплені". Таким чином отримаємо можливість, не розв'язуючи задачі, визначити оптимальні значення частини змінних , незалежно від реалізації випадкових параметрів умов задачі. Маючи на увазі, крім цього, співвідношення (4.8), отримаємо таблицю 4.1.
Використовуючи таблицю 4.1. можна спростити рівняння і нерівності, які визначають сім (по числу Sk) можливих багатогранних множин оптимальних планів задачі (4.3)-(4.7). Маємо:
Неможливо розібрати вираз (невідома помилка): \begin{cases} p_2(u_2^2+u_2^4)+ p_4 u_4^4+ p_5 u_5^2+ p_9 u_9^6 =\alpha_1 - p_1 - p_3 - p_6 - p_7,\\ p_2(u_2^2+u_2^4)+ p_4 u_3^4 + p_5 u_5^2+ p_9 u_9^6 =\alpha_2 - p_1 - p_4 - p_6 - p_8,\\ u_2^2 +u_2^3+u_2^4=1, u_3^2+u_3^4 =1, \\ u_4^3 +u_4^4=1, u_5^2+u_5^3 =1,\\ u_9^2 +u_9^6+u_9^7=1, u_i^j \geqslant 0 \end{cases}
(4.19)
Неможливо розібрати вираз (невідома помилка): \begin{cases} p_3(u_3^2+u_3^5)+ p_6 u_6^5+ p_7( u_7^2+u_7^5)+p_9 u_9^5 =1-\alpha_2,\\ p_2u_1^1+ p_3 (u_3^2 u_3^4)+ p_6 u_6^4 + p_7 u_7^2=\alpha_1 \\ u_1^1 +u_1^3=1, u_3^2+u_3^4 + u_3^5+u_3^7=1, \\ u_5^4 +u_6^5+u_6^7=1, u_7^2+u_7^5+u_7^7 =1,\\ u_5^9 +u_9^7=1, u_i^j \geqslant 0 \end{cases}
(4.20)
Таким чином, маємо:
Наслідок 4.2. Множина оптимальних планів задачі (4.3)-(4.7) визначається таблицею 4.1. та однією з систем (4.19)-(4.25) (в залежності від значень α2, α1, та pi).
Теорема 4.3. Якщо задача (4.1)-(4.2) сумісна, то існує ф-я Неможливо розібрати вираз (невідома помилка): x*(\omega)
яка є розв'язком задачі. При цьому, якщо верхня грань цільового функціонала Неможливо розібрати вираз (невідома помилка): S(\alpha_1,\alpha_2) рівна k-му числу системи, яка визначається теоремою 4.2., тоді розв'язки задачі і тільки вони задовольняють умовам (4.2) та k-му рівнянню наступної системи:
Приклад. Розглянемо наступну задачу стохастичного програмування:
Неможливо розібрати вираз (невідома помилка): P\{c(\omega) x(\omega) \geqslant L{\omega) } \rightarrow sup,
(4.26)
Неможливо розібрати вираз (невідома помилка): \begin{cases} P\{A(\omega) x(\omega) \leqslant b{\omega)} \geqslant \alpha_1,\\ P{x(\omega) \geqslant 0} \geqslant \alpha_2\end{cases}
(4.27)
Припускається, що вип. вел. Неможливо розібрати вираз (невідома помилка): L(\omega)
, всі компоненти вип. векторів Неможливо розібрати вираз (невідома помилка): c(\omega) i b(\omega) та елементи вип. матриці Неможливо розібрати вираз (невідома помилка): A(\omega) невід'ємні майже при всіх Неможливо розібрати вираз (невідома помилка): \omega Тоді з ймовірністю 1 множина Неможливо розібрати вираз (невідома помилка): G_1 \cap G_2 \ne \varnothing
.
Нехай крім цього Неможливо розібрати вираз (невідома помилка): P \{ c(\omega) =0. . Це означає, що Неможливо розібрати вираз (невідома помилка): G_1 \cap G_2 \ne \varnothing
з ймовірністю 1.
Таким чином, з 9 ситуацій з додатною ймовірністю з'язляються тільки 3: 1, 2, 4. Тобто: Неможливо розібрати вираз (невідома помилка): p_3=p_5=p_6=p_7=p_8=p_9=0
(4.28)
Неможливо розібрати вираз (невідома помилка): p_1=p_2=p_4=1
(4.29)
Випишемо, враховуючи (4.28)-(4.29), можливі значення верхньої грані цільової функції задачі (4.1)-(4.2):
Очевидно, що Неможливо розібрати вираз (невідома помилка): S_2\geqslant S_1, S_5 \geqslant S_1 . Крім цього, якщо Неможливо розібрати вираз (невідома помилка): S_1 < 1
то Неможливо розібрати вираз (невідома помилка): S_6 , S_1
. Якщо ж Неможливо розібрати вираз (невідома помилка): S_1 \geqslant 1
то Неможливо розібрати вираз (невідома помилка): S_6 \geqslant 1
.Отже, Неможливо розібрати вираз (невідома помилка): S_2 \geqslant S_7 . Тобто оптимальне значення цільової функції задачі (4.1)-(4.2) може дорівнювати одному з 3-х чисел Неможливо розібрати вираз (невідома помилка): S_1, S_4, S_7 . Розглянемо ці випадки послідовно:
А) Неможливо розібрати вираз (невідома помилка): S(\alpha_1,\alpha_2)=S_1= (1-\alpha_1)+(1-\alpha_2)+p_1