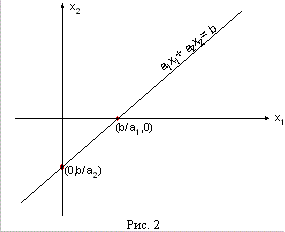Відмінності між версіями «Геометрична інтерпретація задачі лінійного програмування. Графічний метод розв’язування задач лінійного програмування»
Максим (обговорення • внесок) (→Геометрична інтерпретація задач лінійного програмування) |
Максим (обговорення • внесок) (→Геометрична інтерпретація задач лінійного програмування) |
||
| Рядок 1: | Рядок 1: | ||
== Геометрична інтерпретація задач лінійного програмування == | == Геометрична інтерпретація задач лінійного програмування == | ||
| − | Для розуміння всього в подальшого корисно знати і уявляти собі геометричну інтерпретацію завдань лінійного програмування, яку можна дати для випадків n = 2 і n = 3. | + | Для розуміння всього в подальшого корисно знати і уявляти собі геометричну інтерпретацію завдань лінійного програмування, яку можна дати для випадків <math> \ n = 2 </math> і <math> \ n = 3 </math>. |
| − | Найбільш наочна ця інтерпретація для випадку n = 2, тобто для випадку двох змінних і. Нехай нам задана задача лінійного програмування в стандартній формі | + | Найбільш наочна ця інтерпретація для випадку <math> \ n = 2 </math>, тобто для випадку двох змінних і. Нехай нам задана задача лінійного програмування в стандартній формі |
<math>c_1x_1+c_2x_2 \rArr max</math> | <math>c_1x_1+c_2x_2 \rArr max</math> | ||
| Рядок 23: | Рядок 23: | ||
[[Файл:231.gif]] | [[Файл:231.gif]] | ||
| + | |||
| + | Якщо ж <math> \ b = 0 </math>, то на прямий лежить точка (0,0). Щоб знайти іншу точку, можна взяти будь-яке відмінне від нуля значення <math> \ x_1</math> і обчислити відповідне йому значення. | ||
Версія за 15:16, 27 квітня 2012
Геометрична інтерпретація задач лінійного програмування
Для розуміння всього в подальшого корисно знати і уявляти собі геометричну інтерпретацію завдань лінійного програмування, яку можна дати для випадків Неможливо розібрати вираз (невідома помилка): \ n = 2
і Неможливо розібрати вираз (невідома помилка): \ n = 3
.
Найбільш наочна ця інтерпретація для випадку Неможливо розібрати вираз (невідома помилка): \ n = 2 , тобто для випадку двох змінних і. Нехай нам задана задача лінійного програмування в стандартній формі
Неможливо розібрати вираз (невідома помилка): c_1x_1+c_2x_2 \rArr max
Неможливо розібрати вираз (невідома помилка): a_{11}x_1+a_{12}x_2 \le b_1
Неможливо розібрати вираз (невідома помилка): a_{21}x_1+a_{22}x_2 \le b_2
......
Неможливо розібрати вираз (невідома помилка): a_{m1}x_1 + a_{m2}x_2 \le b_m
Візьмемо на площині декартову систему координат і кожній парі чисел поставимо у відповідність точку на цій площині.
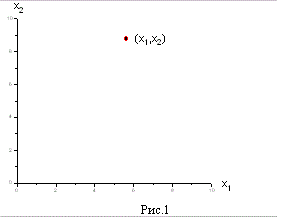
Звернемо насамперед увагу на обмеження Неможливо розібрати вираз (невідома помилка): x_1 \ge 0
і Неможливо розібрати вираз (невідома помилка): x_2 \ge 0 . Вони з усієї площині вирізають лише її першу чверть (див. рис. 1). Розглянемо тепер, які області відповідають нерівностям виду Неможливо розібрати вираз (невідома помилка): a_1x_1+a_2x_2 \ =b
. Спочатку розглянемо область, відповідну рівності Неможливо розібрати вираз (невідома помилка): a_1x_1+a_2x_2 \le =b . Як ви, звичайно, знаєте, це пряма лінія. Будувати її простіше всього по двом точкам.
Нехай Неможливо розібрати вираз (невідома помилка): b \ne 0
. Якщо взяти x_1 , то вийде Неможливо розібрати вираз (невідома помилка): x_2=\frac ba_2 . Якщо взяти , то вийде Неможливо розібрати вираз (невідома помилка): x_1=\frac ba_1 . Таким чином, на прямий лежать дві точки і. Далі через ці дві точки можна по лінійці провести пряму лінію (дивися рисунок 2).
Якщо ж Неможливо розібрати вираз (невідома помилка): \ b = 0 , то на прямий лежить точка (0,0). Щоб знайти іншу точку, можна взяти будь-яке відмінне від нуля значення Неможливо розібрати вираз (невідома помилка): \ x_1
і обчислити відповідне йому значення.