Відмінності між версіями «Золотий перетин»
Andrey (обговорення • внесок) |
Andrey (обговорення • внесок) |
||
| Рядок 1: | Рядок 1: | ||
| − | Золотий перетин — це найкомфортніша для ока пропорція, форма, в основі побудови якої лежить поєднання симетрії і золотого перетину, сприяє якнайкращому зоровому сприйняттю і появі відчуття краси і гармонії. У математиці пропорцією називають рівність двох відносин: a : b = c : d. | + | '''Золотий перетин''' — це найкомфортніша для ока пропорція, форма, в основі побудови якої лежить поєднання симетрії і золотого перетину, сприяє якнайкращому зоровому сприйняттю і появі відчуття краси і гармонії. У математиці пропорцією називають рівність двох відносин: a : b = c : d. |
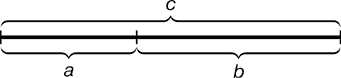
Відрізок прямої AB можна розділити точкою C на дві частини наступними способами: | Відрізок прямої AB можна розділити точкою C на дві частини наступними способами: | ||
Версія за 12:57, 26 листопада 2008
Золотий перетин — це найкомфортніша для ока пропорція, форма, в основі побудови якої лежить поєднання симетрії і золотого перетину, сприяє якнайкращому зоровому сприйняттю і появі відчуття краси і гармонії. У математиці пропорцією називають рівність двох відносин: a : b = c : d.
Відрізок прямої AB можна розділити точкою C на дві частини наступними способами:
- на дві рівні частини AB : АС = АВ : ВС,
- на дві нерівні частини в будь-якому відношенні (такі частини пропорції не утворюють): таким чином, коли АВ : ВС = ВС : АС.
Останнє і є золоте ділення або ділення відрізка в крайньому і середньому відношенні.
Золотий перетин — це таке пропорційне ділення відрізка на нерівні частини, при якому весь відрізок так відноситься до більшої частини, як сама велика частина відноситься до меншої; або іншими словами, менший відрізок так відноситься до більшого, як більший до всього.
а : b = b : c або c : b = b : а.
Відрізки золотої пропорції виражаються нескінченним ірраціональним дробом 0,618..., якщо c прийняти за одиницю, а = 0,382. Відношення ж відрізків а і b складає 1,618. Прямокутник з таким відношенням сторін стали називати золотим прямокутником. Він також володіє цікавими властивостями. Якщо від нього відрізати квадрат, то знову залишиться золотий прямокутник. Цей процес можна продовжувати до безкінечності. А якщо провести діагональ першого і другого прямокутника, то точка їх перетину належатиме всім золотим прямокутникам, які одержали. Є і золотий трикутник (рівнобедрений трикутник, у якого відношення довжини бічної сторони до довжини основи дорівнює 1,618), і золотий кубоїд (прямокутний паралелепіпед з ребрами, що мають довжини 1,618, 1 і 0,618). Золотий перетин не є штучним явищем. Воно дуже широко поширене в природі: золотий перетин можна знайти в пропорціях тіл багатьох рослин і тварин, а також морських раковин і пташиних яєць.
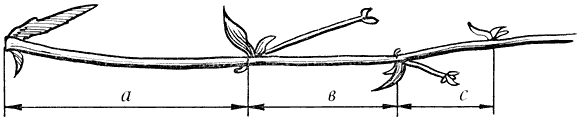
Приклад використання золотого перетину в рослинному світі: цикорій.
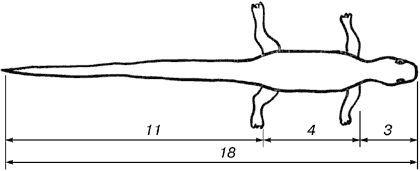
Приклад використання золотого перетину в тваринному світі: ящірка живородюча.
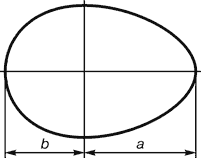
Приклад використання золотого перетину в тваринному світі: пташине яйце.
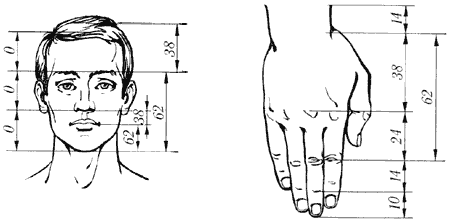
Але найбільш вражаючий приклад "застосування" природою принципу золотого перетину — людське тіло. Воно цілком і його частини (обличчя, руки, грона рук і т. д.) наскрізь пронизані пропорцією 1,618.
Золоті пропорції в частинах тіла людини.
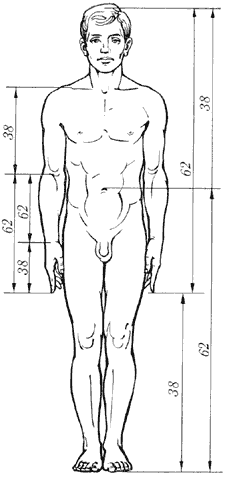
Золоті пропорції в фігурі людини.
Принцип золотого перетину був відкритий людьми ще у глибокій старовині. Знамениті єгипетські піраміди в Гізі, наприклад, засновані на пропорціях золотого перетину. Молодші мексиканські піраміди і античний храм Парфенон також містять в собі пропорцію 1,618.
З золотим перетином пов'язано ім'я італійського математика Фібоначчі. Ряд чисел 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 і т.д. відомий як ряд Фібоначчі. Отримав він цей ряд, розмірковуючи на тему про те, скільки пар кроликів народиться від однієї пари (при місячній розгляді). Кожен член ряду, починаючи з третього, дорівнює сумі двох попередніх, а відношення суміжних чисел ряду наближається до відношенню золотого перетину (21 : 34 = 0,617; 34 : 55 = 0,618). Не зв'язуючи цей ряд із золотим перетином, Фібоначчі відкрив закономірність, до якої незмінно приходили всі дослідники золотого перетину в природі, мистецтві.
З розвитком дизайну і технічної естетики дія закону золотого перетину розповсюдилася на конструювання машин, меблів і т.д. Проектування комп'ютерних інтерфейсів — не виключення. Форми діалогових вікон і елементів управління, сторони яких відносяться як 1,618, дуже привабливі для користувачів. Наприклад, дуже багато захоплень у користувачів програми Chameleon Clock (http://www.softshape.com) викликає така, здавалося б, буденна річ, як вид діалогового вікна Властивості. А все тому, що при його проектуванні використовувався саме принцип золотого перетину.
Продемонструємо на невеликому прикладі, як же застосовується золотий перетин в розробці інтерфейсів.
Припустимо, що ми працюємо в Delphi, і нам потрібно привести до пропорцій золотого перетину діалогове вікно (і його елементи), в якому задаються параметри роботи для розробників програми. У вікні розташовані такі елементи: мітка (TLabel) та рядок введення (TEdit), групбокс (TGroupBox) з двома чекбоксами (TCheckBox) та дві кнопки (TButton) "OK", "Cancel". Після початкового компонування вікна отримуємо варіант 1.