Відмінності між версіями «Стаття проекту " Урок майбутнього!" Леонова Інна»
813899 (обговорення • внесок) (→6. Сприйняття нового матеріалу.) |
813899 (обговорення • внесок) (→6. Сприйняття нового матеріалу.) |
||
| Рядок 66: | Рядок 66: | ||
===6. Сприйняття нового матеріалу.=== | ===6. Сприйняття нового матеріалу.=== | ||
| − | Поверхня циліндра складається з двох рівних основ і бічної поверхні. Якщо поверхню циліндра розрізати по колах основ і одній із твірних, а потім розгорнути на площині, то дістанемо розгортку циліндра (рис.265). вона складається з прямокутника, сторони якого дорівнюють довжині кола основ і висоті циліндра, і двох кругів, що є основами циліндра. | + | [[Файл:П1.png|праворуч|200пкс]] |
| − | + | <big> Поверхня циліндра складається з двох рівних основ і бічної поверхні. Якщо поверхню циліндра розрізати по колах основ і одній із твірних, а потім розгорнути на площині, то дістанемо розгортку циліндра (рис.265). вона складається з прямокутника, сторони якого дорівнюють довжині кола основ і висоті циліндра, і двох кругів, що є основами циліндра.<br /> | |
Площею бічної і повної поверхні циліндра називають площу розгортки бічної і повної поверхонь. | Площею бічної і повної поверхні циліндра називають площу розгортки бічної і повної поверхонь. | ||
Тоді площа бічної повірхні і площа повної поверхні визначаються формулами: | Тоді площа бічної повірхні і площа повної поверхні визначаються формулами: | ||
| + | |||
| + | Sбічн = 2πRH.<br /> | ||
| + | Sцил = Sбічн + 2Sосн, Sцил = 2πRH + 2πR^2 = 2πR(H + R).<br /> | ||
| + | |||
| + | де R, H — радіус і висота циліндра відповідно. | ||
| + | |||
| + | Об'єм циліндра дорівнює добутку площі його основи на висоту V = Sосн ∙ H. | ||
| + | |||
| + | Якщо радіус основи циліндра дорівнює R, а висота Н, то його об'єм | ||
| + | V = πR2H.</big> | ||
Версія за 15:05, 5 червня 2018
Навчальний предмет
Геометрія
Вік учнів, клас
16-18 років, 11 клас
Тема уроку
Циліндр. Об'єм циліндра
Тип уроку
комбінований
Мета уроку
Навчальна мета:
- формування знань учнів про об’єм циліндра та навиків його
обчислення;
- показати застосування циліндра в побуті, техніці;
Розвивальна мета:
- розвивати в учнів логічне мислення,
- увагу,
- просторову уяву,
- уміння знаходити помилки та неточності у відповідях товаришів,
- уміння працювати в групах.
Виховна мета:
- виховувати організованість,
- уміння долати труднощі,
- здатність вибирати необхідну інформацію.
Хід уроку
1. Організаційний етап
Привітання з учнями. Перевірка готовності учнів до уроку. Налаштування на роботу.
Девіз уроку: Ми живемо в геометричний період.
Усе навколо – геометрія.
Ле Корбюзьє
2. Перевірка домашнього завдання.
Перевірити наявність виконаного домашнього завдання та відповісти на запитання учнів, які виникли в них при розв'язуванні задач.
3. Актуалізація опорних знань.
Фронтальна бесіда:
- Заповність пропуски:
- Твірними циліндра називаються ... які сполучають відповідні тчоки ... кіл основи;
- Твірні циліндра ... і ...;
- Поверхня циліндра складається із ... і ...;
- Радіус циліднра - це радіус ...;
- Висотою циліндра називається відстань між ...;
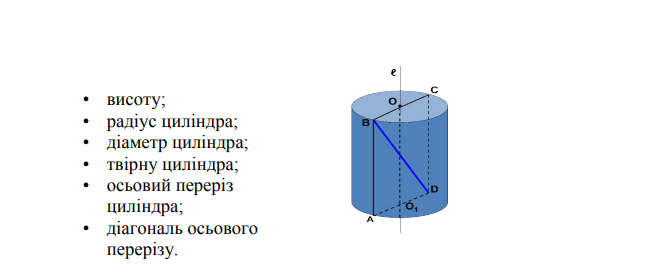
- На даному зображенні циліндра назвіть:
4. Мотивація навчальної діяльності.
Світ, в якому ми живемо, наповнений геометрією будинків і вулиць, творінням природи й людини.
Якщо озирнутися навколо, можна побачити багато речей які мають циліндричну форму.
Це і предмети побуту, продукти харчування, канцелярське та хімічне приладдя, косметичні товари, різноманітні деталі тощо.


На практиці часто виникає потреба знати не тільки яку геометричну форму мають деякі предмети , а й знати їх об'єми.
5. Повіломлення теми, мети і завдань уроку.
Сьогодні ми навчимося знаходити об'єм одного з тіл обертання - циліндра, а також продемонструємо зв'язок математичної теорії з практикою.
6. Сприйняття нового матеріалу.
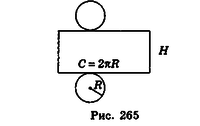
Поверхня циліндра складається з двох рівних основ і бічної поверхні. Якщо поверхню циліндра розрізати по колах основ і одній із твірних, а потім розгорнути на площині, то дістанемо розгортку циліндра (рис.265). вона складається з прямокутника, сторони якого дорівнюють довжині кола основ і висоті циліндра, і двох кругів, що є основами циліндра.
Площею бічної і повної поверхні циліндра називають площу розгортки бічної і повної поверхонь.
Тоді площа бічної повірхні і площа повної поверхні визначаються формулами:
Sбічн = 2πRH.
Sцил = Sбічн + 2Sосн, Sцил = 2πRH + 2πR^2 = 2πR(H + R).
де R, H — радіус і висота циліндра відповідно.
Об'єм циліндра дорівнює добутку площі його основи на висоту V = Sосн ∙ H.
Якщо радіус основи циліндра дорівнює R, а висота Н, то його об'єм V = πR2H.