Відмінності між версіями «Механічні напруження»
| Рядок 10: | Рядок 10: | ||
Розрізняють дві складові вектора механічного напруги: | Розрізняють дві складові вектора механічного напруги: | ||
| − | Нормальне механічне напруження - докладено на одиничну площадку перетину, по нормалі до перетину (позначається | + | Нормальне механічне напруження - докладено на одиничну площадку перетину, по нормалі до перетину (позначається σ ). |
| − | Дотичне механічне напруження - докладено на одиничну площадку перетину, в площині перерізу по дотичній (позначається | + | Дотичне механічне напруження - докладено на одиничну площадку перетину, в площині перерізу по дотичній (позначається τ ). |
Сукупність напружень, що діють за різними майданчикам, проведеним через дану точку, називається напруженим станом у точці. | Сукупність напружень, що діють за різними майданчикам, проведеним через дану точку, називається напруженим станом у точці. | ||
| + | '''В системі СІ механічне напруження вимірюється в паскалях.''' | ||
| + | |||
| + | |||
| + | '''Тензор механічної напруги''' | ||
| + | |||
| + | [[Файл: Stress_tensor.png]] | ||
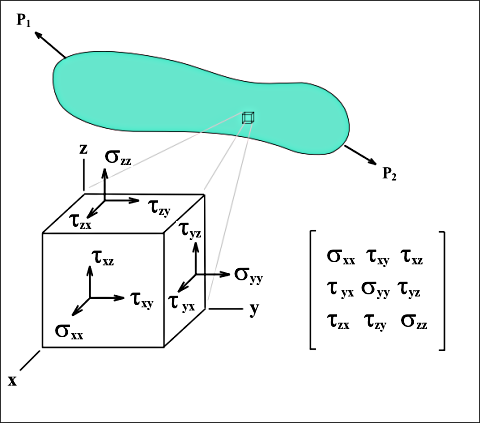
| + | Повний тензор механічної напруги елементарного об'єму тіла. Буквою σ позначені нормальні механічні напруги, а дотичні буквою τ. | ||
| + | |||
| + | Більш строго механічне напруження - тензорна величина. Компоненти тензора напружень σij дорівнюють відношенню компоненти сили ∆F_i , Що діє на елементарну площадку ∆S до її площі: | ||
| + | |||
| + | σij = ∆F_i/∆S_j | ||
| + | |||
| + | Тут під ∆S_j розуміються компоненти вектора, утвореного із нормалі до елементарної майданчику n ⃗ і її площі ∆S : | ||
| + | |||
| + | ∆S ⃗= n ⃗∆S | ||
| + | |||
| + | Таким чином сила, що діє на якийсь обсяг V дорівнює інтегралу тензора напруги на кордоні цього обсягу по поверхні цього обсягу S (За відсутності об'ємних сил): | ||
| + | |||
| + | Fi=∮_S▒〖σ_ij dS_j 〗 | ||
Поточна версія на 20:58, 19 травня 2013
Механічне напруга - це міра внутрішніх сил, що виникають в деформується тілі під впливом різних факторів. Механічне напруження в точці тіла визначається як відношення внутрішньої сили до одиниці площі в даній точці розглянутого перерізу.
Напруження є результатом взаємодії частинок тіла при його навантаженні. Зовнішні сили прагнуть змінити взаємне розташування частинок, а виникаючі при цьому напруги перешкоджають зсуву часток, обмежуючи його в більшості випадків деякою малою величиною.
Q =F/S Q - механічне напруження. F - сила, що виникла в тілі при деформації. S - площа.
Розрізняють дві складові вектора механічного напруги:
Нормальне механічне напруження - докладено на одиничну площадку перетину, по нормалі до перетину (позначається σ ). Дотичне механічне напруження - докладено на одиничну площадку перетину, в площині перерізу по дотичній (позначається τ ).
Сукупність напружень, що діють за різними майданчикам, проведеним через дану точку, називається напруженим станом у точці.
В системі СІ механічне напруження вимірюється в паскалях.
Тензор механічної напруги
Повний тензор механічної напруги елементарного об'єму тіла. Буквою σ позначені нормальні механічні напруги, а дотичні буквою τ.
Більш строго механічне напруження - тензорна величина. Компоненти тензора напружень σij дорівнюють відношенню компоненти сили ∆F_i , Що діє на елементарну площадку ∆S до її площі:
σij = ∆F_i/∆S_j
Тут під ∆S_j розуміються компоненти вектора, утвореного із нормалі до елементарної майданчику n ⃗ і її площі ∆S :
∆S ⃗= n ⃗∆S
Таким чином сила, що діє на якийсь обсяг V дорівнює інтегралу тензора напруги на кордоні цього обсягу по поверхні цього обсягу S (За відсутності об'ємних сил):
Fi=∮_S▒〖σ_ij dS_j 〗