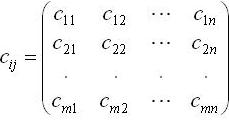Відмінності між версіями «Економічна і математична постановка ТЗ.»
Матеріал з Вікі ЦДУ
| Рядок 1: | Рядок 1: | ||
Класична транспортна задача лінійного програмування фор-мулюється так: деякий однорідний продукт, що знаходиться у m постачальників Аі в обсягах <math>a_{1} ,a_{2} ,...,a_{m}</math> одиниць відповідно необ-хідно перевезти n споживачам Bj в обсягах <math>b_{1} ,b_{2} ,...,b_{n}</math> одиниць. При цьому виконується умова, що загальний наявний обсяг про-дукції у постачальників дорівнює загальному попиту всіх спожи-вачів. Відомі вартості Cij перевезень одиниці продукції від кож-ного Аі-го постачальника до кожного Вj-го споживача, що подані як елементи матриці виду: | Класична транспортна задача лінійного програмування фор-мулюється так: деякий однорідний продукт, що знаходиться у m постачальників Аі в обсягах <math>a_{1} ,a_{2} ,...,a_{m}</math> одиниць відповідно необ-хідно перевезти n споживачам Bj в обсягах <math>b_{1} ,b_{2} ,...,b_{n}</math> одиниць. При цьому виконується умова, що загальний наявний обсяг про-дукції у постачальників дорівнює загальному попиту всіх спожи-вачів. Відомі вартості Cij перевезень одиниці продукції від кож-ного Аі-го постачальника до кожного Вj-го споживача, що подані як елементи матриці виду: | ||
[[Файл:Безымяннывй.JPG]] | [[Файл:Безымяннывй.JPG]] | ||
| + | |||
Необхідно визначити план перевезень, за якого вся продукція була б вивезена від постачальників, повністю задоволені потреби споживачів і загальна вартість всіх перевезень була б мінімаль-ною. | Необхідно визначити план перевезень, за якого вся продукція була б вивезена від постачальників, повністю задоволені потреби споживачів і загальна вартість всіх перевезень була б мінімаль-ною. | ||
У такій постановці задачі ефективність плану перевезень ви-значається його вартістю і така задача має назву транспортної задачі за критерієм вартості перевезень. | У такій постановці задачі ефективність плану перевезень ви-значається його вартістю і така задача має назву транспортної задачі за критерієм вартості перевезень. | ||
| + | |||
| + | Позначимо через <math>x_{ij}</math> <math>A_{i}</math> | ||
Версія за 14:09, 16 травня 2012
Класична транспортна задача лінійного програмування фор-мулюється так: деякий однорідний продукт, що знаходиться у m постачальників Аі в обсягах Неможливо розібрати вираз (невідома помилка): a_{1} ,a_{2} ,...,a_{m}
одиниць відповідно необ-хідно перевезти n споживачам Bj в обсягах Неможливо розібрати вираз (невідома помилка): b_{1} ,b_{2} ,...,b_{n}
одиниць. При цьому виконується умова, що загальний наявний обсяг про-дукції у постачальників дорівнює загальному попиту всіх спожи-вачів. Відомі вартості Cij перевезень одиниці продукції від кож-ного Аі-го постачальника до кожного Вj-го споживача, що подані як елементи матриці виду:
Необхідно визначити план перевезень, за якого вся продукція була б вивезена від постачальників, повністю задоволені потреби споживачів і загальна вартість всіх перевезень була б мінімаль-ною. У такій постановці задачі ефективність плану перевезень ви-значається його вартістю і така задача має назву транспортної задачі за критерієм вартості перевезень.
Позначимо через Неможливо розібрати вираз (невідома помилка): x_{ij}
Неможливо розібрати вираз (невідома помилка): A_{i}