Відмінності між версіями «Інтеграли Френеля та інтеграл ймовірностей»
| Рядок 1: | Рядок 1: | ||
| − | [[Файл:Fresnel Integrals (Unnormalised).svg|250px|thumb| | + | [[Файл:250px-Fresnel Integrals (Unnormalised).svg.png|250px|thumb| |
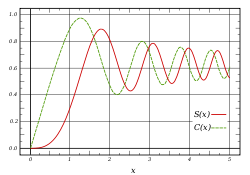
<font color=#b30000>''S''(''x'')</font> и <font color=#00b300>''C''(''x'')</font>. Максимальное значение для ''C''(''x'') примерно равно 0.977451424. Если использовать <math>\pi t^2</math> вместо <math>t^2</math>, то график изменит вертикальный и горизонтальный масштаб (см. ниже).]] | <font color=#b30000>''S''(''x'')</font> и <font color=#00b300>''C''(''x'')</font>. Максимальное значение для ''C''(''x'') примерно равно 0.977451424. Если использовать <math>\pi t^2</math> вместо <math>t^2</math>, то график изменит вертикальный и горизонтальный масштаб (см. ниже).]] | ||
Версія за 20:13, 20 травня 2010
Интегралы Френеля S(x) и C(x) — это специальные функции, названные в честь Огюстена Жана Френеля и используемые в оптике. Они возникают при расчёте дифракции Френеля и определяются как
- Неможливо розібрати вираз (невідома помилка): S(x)=\int\limits_0^x \sin(t^2)\,dt,\quad C(x)=\int\limits_0^x \cos(t^2)\,dt.
Параметрический график S(x) и C(x) даёт кривую на плоскости, называемую спиралью Корню или клотоидой.
Зміст
Разложение в ряд
, а не Неможливо розібрати вираз (невідома помилка): t^2
, как на рисунке выше.Интегралы Френеля могут быть представлены степенными рядами, сходящимися при всех x:
- Неможливо розібрати вираз (невідома помилка): S(x)=\int\limits_0^x \sin(t^2)\,dt=\sum_{n=0}^{\infin}(-1)^n\frac{x^{4n+3}}{(4n+3)(2n+1)!},
- Неможливо розібрати вираз (невідома помилка): C(x)=\int\limits_0^x \cos(t^2)\,dt=\sum_{n=0}^{\infin}(-1)^n\frac{x^{4n+1}}{(4n+1)(2n)!}.
Некоторые авторы[1] используют в качестве аргумента тригонометрических подынтегральных функций Неможливо розібрати вираз (невідома помилка): \frac{\pi}{2}t^2
. Полученные функции получаются из определённых выше сжатием графика по оси Y в Неможливо розібрати вираз (невідома помилка): \sqrt{\frac{2}{\pi}}
раз и растяжением вдоль оси X во столько же раз.
Спираль Корню
Шаблон:Основная статья Спираль Корню, также известная как клотоида, — это кривая, являющаяся параметрическим графиком S(t) от C(t). Спираль Корню была придумана Мари Альфредом Корню для облегчения расчёта дифракции в прикладных задачах.
Так как
- Неможливо розібрати вираз (невідома помилка): C\,'(t)^2 + S\,'(t)^2 = \sin^2(t^2) + \cos^2(t^2) = 1,
то в такой параметризации касательный вектор имеет единичную длину, так что t является длиной кривой, измеряемой от точки (0,0). Следовательно, обе ветви спирали имеют бесконечную длину.
Кривизна этой кривой в любой точке пропорциональна длине дуги, заключённой между этой точкой и началом координат. Благодаря этому свойству она применяется в строительстве дорог, так как угловое ускорение машины, движущейся по этой кривой с постоянной скоростью, будет изменяться линейно
Свойства
- C(x) и S(x) — нечётные функции x.
- Используя разложение в ряд, можно построить аналитическое продолжение интегралов Френеля на всю комплексную плоскость. Комплексные интегралы Френеля выражаются через функцию ошибок как
- Неможливо розібрати вираз (невідома помилка): S(x)=\frac{\sqrt{\pi}}{4} \left( \sqrt{i}\,\mathrm{erf}(\sqrt{i}\,x) + \sqrt{-i}\,\mathrm{erf}(\sqrt{-i}\,x) \right)
- Неможливо розібрати вираз (невідома помилка): C(x)=\frac{\sqrt{\pi}}{4} \left( \sqrt{-i}\,\mathrm{erf}(\sqrt{i}\,x) + \sqrt{i}\,\mathrm{erf}(\sqrt{-i}\,x) \right)
.
- Интегралы Френеля не выражаются через элементарные функции, кроме частных случаев. Предел этих функций при Неможливо розібрати вираз (невідома помилка): x \rightarrow \infty
равен
- Неможливо розібрати вираз (невідома помилка): \int\limits_{0}^{\infty} \cos t^2\,dt = \int\limits_{0}^{\infty} \sin t^2\,dt = \frac{\sqrt{2\pi}}{4} = \sqrt{\frac{\pi}{8}}.
Вычисление
Пределы функций C и S при Неможливо розібрати вираз (невідома помилка): x \rightarrow \infty
могут быть найдены с помощью контурного интегрирования. Для этого берётся контурный интеграл функции
- Неможливо розібрати вираз (невідома помилка): e^{-\frac{1}{2}t^2}
по границе сектора на комплексной плоскости, образованного осью абсцисс, лучом Неможливо розібрати вираз (невідома помилка): y=x
, Неможливо розібрати вираз (невідома помилка): x \geqslant 0
и окружностью радиуса R с центром в начале координат.
При Неможливо розібрати вираз (невідома помилка): R \rightarrow \infty
интеграл по дуге стремится к 0, интеграл по вещественной оси стремится к значению интеграла Пуассона
- Неможливо розібрати вираз (невідома помилка): \int\limits_{0}^{\infty} e^{-\frac{1}{2}t^2}dt = \sqrt{\frac {\pi}{2}},
и, после некоторых преобразований, интеграл вдоль оставшегося луча может быть выражен через предельное значение интеграла Френеля.
См. также
Примечания
- Milton Abramowitz and Irene A. Stegun, eds. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. — New York: Dover, 1972. (См. часть 7) Шаблон:Ref-en
Внешние ссылки
- Шаблон:MathWorld Шаблон:Ref-en
- Шаблон:MathWorld Шаблон:Ref-en
- R. Nave, The Cornu spiral, Hyperphysics (2002) (Использует πt²/2 вместо t².) Шаблон:Ref-en
- Шаблон:Cite web Шаблон:Ref-en
Категория:Физическая оптика Категория:Специальные функции
en:Fresnel integral
Помилка цитування: Для наявного тегу <ref> не знайдено відповідного тегу <references/>