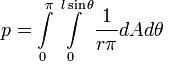Відмінності між версіями «Метод статистичних випробовувань»
| (не показано одну проміжну версію цього учасника) | |||
| Рядок 1: | Рядок 1: | ||
| − | '''Метод Монте-Карло''' (за назвою міста, яке відоме своїми гральними домами) — загальна назва групи числових методів, | + | '''Метод Монте-Карло''' (за назвою міста, яке відоме своїми гральними домами) — загальна назва групи числових методів, заснованих на одержанні великої кількості реалізацій стохастичного (випадкового) процесу, який формується у той спосіб, щоб його імовірнісні характеристики збыгалися з аналогічними величинами задачі, яка вирішується. Використовується для вирішення задач у фізиці, математиці, економіці, оптимізації, теорії управління тощо. |
'''Метод Монте-Карло''' — це метод імітації для приблизного відтворення реальних явищ. Він об'єднує аналіз чутливості (сприйнятливості) і аналіз розподілювання ймовірностей вхідних змінних. Цей метод дає змогу побудувати модель, мінімізуючи дані, а також максимізувати значення даних, які використовуються в моделі. Побудова моделі починається з визначення функціональних залежностей у реальній системі. Після чого можна одержати кількісне рішення, використовуючи теорію ймовірності й таблиці випадкових чисел. | '''Метод Монте-Карло''' — це метод імітації для приблизного відтворення реальних явищ. Він об'єднує аналіз чутливості (сприйнятливості) і аналіз розподілювання ймовірностей вхідних змінних. Цей метод дає змогу побудувати модель, мінімізуючи дані, а також максимізувати значення даних, які використовуються в моделі. Побудова моделі починається з визначення функціональних залежностей у реальній системі. Після чого можна одержати кількісне рішення, використовуючи теорію ймовірності й таблиці випадкових чисел. | ||
| Рядок 23: | Рядок 23: | ||
3. Оскільки дві області знаходяться в співвідношенні π / 4 , об'єкти повинні потрапити в області приблизно в тій же пропорції. Таким чином, підрахувавши кількість об'єктів в колі і розділити на загальну кількість об'єктів в квадраті, отримаємо наближене значення π / 4. | 3. Оскільки дві області знаходяться в співвідношенні π / 4 , об'єкти повинні потрапити в області приблизно в тій же пропорції. Таким чином, підрахувавши кількість об'єктів в колі і розділити на загальну кількість об'єктів в квадраті, отримаємо наближене значення π / 4. | ||
| − | 4. Помноживши результат на 4 | + | 4. Помноживши результат на 4, отримаємо наближене значення власне самого π. |
== Історія == | == Історія == | ||
=== Алгоритм Буффона для визначення числа Пі === | === Алгоритм Буффона для визначення числа Пі === | ||
| − | Випадкові величини використовувалися для вирішення різних прикладних завдань достатньо давно. Прикладом може служити спосіб визначення числа Пі, який був запропонований Буффоном ще в 1777 році. Суть методу була в киданні голки довжиною L на | + | Випадкові величини використовувалися для вирішення різних прикладних завдань достатньо давно. Прикладом може служити спосіб визначення числа Пі, який був запропонований Буффоном ще в 1777 році. Суть методу була в киданні голки довжиною L на площину, розкреслену паралельними прямими, розташованими на відстані r один від одного (див. Рис. 1). [[Image:Buffon_Pi.jpg|thumb|200px|'''Рисунок 1.''' Метод Буффона]] Вірогідність (як видно з подальшого контексту, йдеться не про вірогідність, а про математичне чекання кількості перетинів за один дослід; вірогідністю це стає лише за умови, що L) того, що відрізок пересіче пряму, пов'язана з числом Пі: |
[[Image:Int11.JPG]], | [[Image:Int11.JPG]], | ||
де | де | ||
| − | * A — відстань від початку голки до | + | * A — відстань від початку голки до найближчої до неї прямої; |
* O — кут голки відносно прямих. | * O — кут голки відносно прямих. | ||
Цей інтеграл легко взяти: [[Image:Int22.JPG]] (при умові, що r > L) тому підрахувавши долю відрізків, що пересікають прямі, можна приблизно визначити це число. При збільшенні кількості спроб точність отримуваного результату збільшуватиметься. | Цей інтеграл легко взяти: [[Image:Int22.JPG]] (при умові, що r > L) тому підрахувавши долю відрізків, що пересікають прямі, можна приблизно визначити це число. При збільшенні кількості спроб точність отримуваного результату збільшуватиметься. | ||
| − | У 1864 році капітан Фокс, видужуючи після поранення, щоб якось зайняти себе, реалізував експеримент по киданню голки. Результати представлені в | + | У 1864 році капітан Фокс, видужуючи після поранення, щоб якось зайняти себе, реалізував експеримент по киданню голки. Результати представлені в таблиці: |
<TABLE width="100%" height="1%" BORDER=1 CELLPADdING=0> | <TABLE width="100%" height="1%" BORDER=1 CELLPADdING=0> | ||
| Рядок 83: | Рядок 83: | ||
Коментарі: | Коментарі: | ||
* Обертання плоскості застосовувалося (і як показують результати — успішно) для того, щоб зменшити систематичну помилку. | * Обертання плоскості застосовувалося (і як показують результати — успішно) для того, щоб зменшити систематичну помилку. | ||
| − | * У третій спробі довжина голки була більше | + | * У третій спробі довжина голки була більше за відстань між лініями, що дозволило не збільшуючи числа кидань ефективно збільшити число подій і підвищити точність. |
=== Зв'язок стохастичних процесів і диференціальних рівнянь === | === Зв'язок стохастичних процесів і диференціальних рівнянь === | ||
| − | Створення математичного апарату стохастичних методів почалося в кінці 19-го століття. У 1899 році лорд Релей показав, що одновимірне випадкове блукання на | + | Створення математичного апарату стохастичних методів почалося в кінці 19-го століття. У 1899 році лорд Релей показав, що одновимірне випадкове блукання на безкінечних гратах може давати наближене вирішення параболічного диференціального рівняння. Андрій Колмогоров в 1931 році дав великий поштовх розвитку стохастичних підходів до вирішення різних математичних завдань, оскільки він зумів довести, що ланцюги Маркова пов'язані з деякими інтегро-дифференціальними рівняннями. У 1933 році Іван Петровський показав, що випадкове блукання, створююче Марківський ланцюг, асимптотика пов'язане з вирішенням еліптичного диференціального рівняння в частинних похідних. Після цих відкриттів стало зрозуміло, що стохастичні процеси можна описувати диференціальними рівняннями і, відповідно, досліджувати при допомозі добре на той момент розроблених математичних методів вирішення цих рівнянь. |
| − | === Народження методу Монте-Карло в Лос- | + | === Народження методу Монте-Карло в Лос-Аламосі === |
| − | Спочатку Енріко Фермі в 1930-х роках в Італії, а потім Джон фон Нейман і Станіслав Улам в 1940-х в Лос- | + | Спочатку Енріко Фермі в 1930-х роках в Італії, а потім Джон фон Нейман і Станіслав Улам в 1940-х в Лос-Аламосі передбачили, що можна використовувати зв'язок між стохастичними процесами і диференціальними рівняннями «у зворотний бік». Вони запропонували використовувати стохастичний підхід для апроксимації багатовимірних інтегралів в рівняннях перенесення, що виникли у зв'язку із завданням про рух нейтрона в ізотропному середовищі. |
| − | Ідея була розвинена Уламом, який, за іронією долі, також як і Фокс боровся з вимушеним неробством під час одужання після хвороби, і, розкладаючи пасьянси, задався питанням, яка вірогідність того, що пасьянс «складеться». Йому в голову прийшла ідея, що замість того, щоб використовувати звичайні для подібних завдань міркування комбінаторики, можна просто поставити «експеримент» велике число разів і, таким чином, підрахувавши число вдалих результатів, оцінити їх вірогідність. Він же запропонував використовувати комп'ютери для розрахунків методом Монте-Карло. | + | Ідея була розвинена Уламом, який, за іронією долі, також, як і Фокс, боровся з вимушеним неробством під час одужання після хвороби, і, розкладаючи пасьянси, задався питанням, яка вірогідність того, що пасьянс «складеться». Йому в голову прийшла ідея, що замість того, щоб використовувати звичайні для подібних завдань міркування комбінаторики, можна просто поставити «експеримент» велике число разів і, таким чином, підрахувавши число вдалих результатів, оцінити їх вірогідність. Він же запропонував використовувати комп'ютери для розрахунків методом Монте-Карло. |
| − | Поява перших електронних комп'ютерів, які могли з великою швидкістю генерувати псевдовипадкові числа, різко розширила круг завдань, для вирішення яких стохастичний підхід виявився ефективнішим, ніж інші математичні методи. Після цього стався великий прорив і метод Монте-Карло застосовувався в багатьох завданнях, проте його використання не завжди було виправдане через велику кількість обчислень, необхідних для здобуття відповіді із заданою точністю. | + | Поява перших електронних комп'ютерів, які могли з великою швидкістю генерувати псевдовипадкові числа, різко розширила круг завдань, для вирішення яких стохастичний підхід виявився ефективнішим, ніж інші математичні методи. Після цього стався великий прорив, і метод Монте-Карло застосовувався в багатьох завданнях, проте його використання не завжди було виправдане через велику кількість обчислень, необхідних для здобуття відповіді із заданою точністю. |
| − | Роком народження методу Монте-Карло вважається 1949 рік, коли в світ виходить стаття Метрополіса і Улама «Метод Монте-Карло». Назва методу походить від назви міста в князівстві Монако, широко відомого своїми багаточисельними казино, оскільки саме рулетка є одним з | + | Роком народження методу Монте-Карло вважається 1949 рік, коли в світ виходить стаття Метрополіса і Улама «Метод Монте-Карло». Назва методу походить від назви міста в князівстві Монако, широко відомого своїми багаточисельними казино, оскільки саме рулетка є одним з найвідоміших генераторів випадкових чисел. Станіслав Улам пише в своїй автобіографії «Пригоди математика», що назва була запропонована Ніколасом Метрополісом на честь його дядька, який був азартним гравцем. |
=== Подальший розвиток і сучасність === | === Подальший розвиток і сучасність === | ||
У 1950-х роках метод використовувався для розрахунків при розробці водневої бомби. Основні заслуги в розвитку методу в цей час належать співробітникам лабораторій ВПС США і корпорації RAND. | У 1950-х роках метод використовувався для розрахунків при розробці водневої бомби. Основні заслуги в розвитку методу в цей час належать співробітникам лабораторій ВПС США і корпорації RAND. | ||
| − | У 1970-х роках в нової області математики — теорії обчислювальної складності було показано, що існує клас завдань, складність (кількість обчислень, необхідних для здобуття точної відповіді) яких зростає з розмірністю завдання експоненціально. Інколи можна, пожертвувавши точністю, знайти алгоритм, складність якого зростає повільніше, але є велика кількість завдань, для якої цього не можна зробити (наприклад, завдання визначення об'єму опуклого тіла в ''''n''''- | + | У 1970-х роках в нової області математики — теорії обчислювальної складності було показано, що існує клас завдань, складність (кількість обчислень, необхідних для здобуття точної відповіді) яких зростає з розмірністю завдання експоненціально. Інколи можна, пожертвувавши точністю, знайти алгоритм, складність якого зростає повільніше, але є велика кількість завдань, для якої цього не можна зробити (наприклад, завдання визначення об'єму опуклого тіла в ''''n''''-мірному евклідовому просторі) і метод Монте-Карло є єдиною можливістю для здобуття досить точної відповіді за прийнятний час. |
В даний час основні зусилля дослідників направлені на створення ефективних Монте-Карло алгоритмів різних фізичних, хімічних і соціальних процесів для паралельних обчислювальних систем. | В даний час основні зусилля дослідників направлені на створення ефективних Монте-Карло алгоритмів різних фізичних, хімічних і соціальних процесів для паралельних обчислювальних систем. | ||
| Рядок 108: | Рядок 108: | ||
Припустимо, необхідно взяти інтеграл від деякої функції. Скористаємося неформальним геометричним описом інтеграла і розумітимемо його як площа під графіком цієї функції. | Припустимо, необхідно взяти інтеграл від деякої функції. Скористаємося неформальним геометричним описом інтеграла і розумітимемо його як площа під графіком цієї функції. | ||
| − | Для визначення цієї площі можна скористатися одним із звичайних чисельних методів інтеграції: розбити відрізок на підвідрізки, підрахувати площу під графіком функції на кожному з них і скласти. Передбачимо, що для функції, представленої на малюнку 2, досить розбиття на 25 відрізків | + | Для визначення цієї площі можна скористатися одним із звичайних чисельних методів інтеграції: розбити відрізок на підвідрізки, підрахувати площу під графіком функції на кожному з них і скласти. Передбачимо, що для функції, представленої на малюнку 2, досить розбиття на 25 відрізків і, отже, обчислення 25 значень функції. Представимо тепер, ми маємо справу з n-мірною функцією. Тоді нам необхідно 25^n відрізків і стільки ж обчислень значення функції. При розмірності функції більше 10 завдання стає величезним. Оскільки простори великої розмірності зустрічаються, зокрема, в завданнях теорії струн, а також багатьох інших фізичних завданнях, де є системи з багатьма мірами свободи, необхідно мати метод рішення,який би не настільки сильно залежав від розмірності. Саме такою властивістю володіє метод Монте-Карло. |
=== Звичайний алгоритм Монте-Карло інтегрування === | === Звичайний алгоритм Монте-Карло інтегрування === | ||
| Рядок 134: | Рядок 134: | ||
Традиційно метод Монте-Карло застосовувався для визначення різних фізичних параметрів систем, що знаходяться в стані термодинамічної рівноваги. Припустимо є набір W(S) можливих станів фізичної системи S. Для визначення середнього значення [[Image:Aover.JPG]] деякої величини A необхідно розрахувати [[Image:Summ.JPG]], где підсумовування виробляється по тих, що всім складаються '''S''' з '''W(S)''', '''P(S)''' — вірогідність стану '''S'''. | Традиційно метод Монте-Карло застосовувався для визначення різних фізичних параметрів систем, що знаходяться в стані термодинамічної рівноваги. Припустимо є набір W(S) можливих станів фізичної системи S. Для визначення середнього значення [[Image:Aover.JPG]] деякої величини A необхідно розрахувати [[Image:Summ.JPG]], где підсумовування виробляється по тих, що всім складаються '''S''' з '''W(S)''', '''P(S)''' — вірогідність стану '''S'''. | ||
| − | === Динамічне ( | + | === Динамічне (кінетичне) формулювання === |
=== Пряме моделювання методом Монте-Карло === | === Пряме моделювання методом Монте-Карло === | ||
| Рядок 142: | Рядок 142: | ||
* Моделювання опромінення твердих тіл іонами в наближенні бінарних зіткнень. | * Моделювання опромінення твердих тіл іонами в наближенні бінарних зіткнень. | ||
* Пряме Монте-Карло моделювання розріджених газів. | * Пряме Монте-Карло моделювання розріджених газів. | ||
| − | * Більшість кінетичних Монте-Карло моделей належать до прямих (зокрема, дослідження молекулярно-пучкової | + | * Більшість кінетичних Монте-Карло моделей належать до прямих (зокрема, дослідження молекулярно-пучкової епітакси). |
=== Квантовий метод Монте-Карло === | === Квантовий метод Монте-Карло === | ||
| Рядок 162: | Рядок 162: | ||
Імітаційні (алгоритмічні) моделі можуть бути детермінованими і стохастичними. В останньому випадку за допомогою датчиків (генераторів) випадкових чисел імітується вплив (дія) невизначених і випадкових чинників. Такий метод імітаційного моде¬лювання дістав назву методу статистичного моделювання (статистичних прогонів, чи методу Монте-Карло). На даний час цей метод вважають одним із найефективніших методів дослідження складних систем, а часто і єдиним практично доступним методом отримання нової інформації щодо поведінки гіпотетичної системи (на етапі її проектування). | Імітаційні (алгоритмічні) моделі можуть бути детермінованими і стохастичними. В останньому випадку за допомогою датчиків (генераторів) випадкових чисел імітується вплив (дія) невизначених і випадкових чинників. Такий метод імітаційного моде¬лювання дістав назву методу статистичного моделювання (статистичних прогонів, чи методу Монте-Карло). На даний час цей метод вважають одним із найефективніших методів дослідження складних систем, а часто і єдиним практично доступним методом отримання нової інформації щодо поведінки гіпотетичної системи (на етапі її проектування). | ||
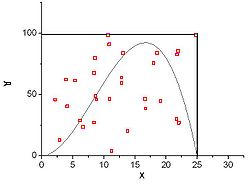
| − | Винахідником методу Монте-Карло називають Станіслава Улама (Stanislaw Ulam), американського математика, який народився у м. Львові. С.Улам перш за все відомий як | + | [[Image:Imagesmmc2013.jpg|thumb|300px|Приклад графічної інтерпретації методу, застосованої до комбінації залежностей]] |
| + | |||
| + | Винахідником методу Монте-Карло називають Станіслава Улама (Stanislaw Ulam), американського математика, який народився у м. Львові. С.Улам перш за все відомий як людина, яка брала участь в проектуванні водневої бомби з Едуардом Теллером на початку 50-х років. Під час II Світової Війни Станіслав Марцин Улам і Джон фон Нейман (Neumann) працювали в Лос-Аламосі на Манхеттенському Проекті над моделюванням нейтронної дифузії в розщеплюваному матеріалі. Метод Монте-Карло він винайшов в 1946 р., коли одужуючи після хвороби, і, розкладаючи пасьянси, задався питанням, яка вірогідність того, що пасьянс «складеться». Йому в голову прийшла ідея, що замість того, щоб використовувати звичайні для подібних завдань міркування комбінаторики, можна просто поставити «експеримент» велике число раз і, таким чином, підрахувавши число вдалих результатів, оцінити їх вірогідність. Він же запропонував використовувати комп'ютери для розрахунків методом Монте-Карло. Працюючи з Джоном фон Нейманом і Ніколасом Метрополісом (N. Metropolis), він розвивав алгоритми для комп'ютерних виконань, також як і досліджував засіб перетворення не випадкових проблем у випадкові форми, які полегшили б їх розв’язок через статистичне здійснення вибірки. Ця робота перетворила статистичне здійснення вибірки з математичної цікавості на формальну методологію, що застосовується до широкого кола різноманітних проблем. Поява перших електронних комп'ютерів, які могли з великою швидкістю генерувати псевдовипадкові числа, різко розширила круг завдань, для вирішення яких стохастичний підхід виявився ефективнішим, ніж інші математичні методи. Після цього відбувся великий прорив і метод Монте-Карло застосовувався в багатьох завданнях, проте його використання не завжди було виправдано через велику кількість обчислень, необхідних для отримання відповіді із заданою точністю. | ||
| + | |||
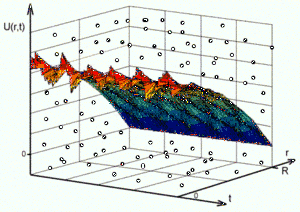
| + | [[Image:A17 i03mmc2013.gif|thumb|300px|Приклад графічної інтерпретації методу у тривимірному просторі]] | ||
Метод Монте-Карло — це сукупність формальних процедур, засобами яких відтворюються на ЕОМ будь-які випадкові фактори (випадкові події, випадкові величини з довільним розподілом, випадкові вектори тощо). У межах цього підходу будується ймовірнісна модель, яка відповідає математичній чи фізичній задачі, і на ній реалізується випадкова вибірка. «Розігрування» вибірок за методом Монте-Карло є основним принципом імітаційного моделювання систем із стохастичними (випадковими, імовірними) елементами. | Метод Монте-Карло — це сукупність формальних процедур, засобами яких відтворюються на ЕОМ будь-які випадкові фактори (випадкові події, випадкові величини з довільним розподілом, випадкові вектори тощо). У межах цього підходу будується ймовірнісна модель, яка відповідає математичній чи фізичній задачі, і на ній реалізується випадкова вибірка. «Розігрування» вибірок за методом Монте-Карло є основним принципом імітаційного моделювання систем із стохастичними (випадковими, імовірними) елементами. | ||
Метод Монте-Карло — це метод імітації для приблизного відтворення реальних явищ. Він об'єднує аналіз чутливості (сприйнятливості) і аналіз розподілювання ймовірностей вхідних змінних. Цей метод дає змогу побудувати модель, мінімізуючи дані, а також максимізувати значення даних, які використовуються в моделі. Побудова моделі починається з визначення функціональних залежностей у реальній системі. Після чого можна одержати кількісне рішення, використовуючи теорію ймовірності й таблиці випадкових чисел. [2, стр.70] | Метод Монте-Карло — це метод імітації для приблизного відтворення реальних явищ. Він об'єднує аналіз чутливості (сприйнятливості) і аналіз розподілювання ймовірностей вхідних змінних. Цей метод дає змогу побудувати модель, мінімізуючи дані, а також максимізувати значення даних, які використовуються в моделі. Побудова моделі починається з визначення функціональних залежностей у реальній системі. Після чого можна одержати кількісне рішення, використовуючи теорію ймовірності й таблиці випадкових чисел. [2, стр.70] | ||
| − | Метод статистичного моделювання (чи метод Монте- | + | Метод статистичного моделювання (чи метод Монте-Карло) — це спосіб дослідження невизначених (стохастичних) економічних об’єктів і процесів, коли не повністю (до певної міри) є відомими внутрішні взаємодії в цих системах. |
| − | Цей метод полягає у модельному відтворенні процесу за допомогою стохастичної математичної моделі та обчисленні характеристик цього процесу. Одне таке відтворення можливого (випадкового) стану функціонування модельованої системи | + | Цей метод полягає у модельному відтворенні процесу за допомогою стохастичної математичної моделі та обчисленні характеристик цього процесу. Одне таке відтворення можливого (випадкового) стану функціонування модельованої системи називають реалізацією (чи імітаційним прогоном).Після кожного прогону реєструють сукупність параметрів, що характеризують випадкову подію (її реалізацію). Метод ґрунтується на багатократних прогонах (випадкових реалізаціях) на підставі побудованої моделі з подальшим статистичним опрацюванням отриманих даних з метою визначення числових характеристик досліджуваного об’єкта (процесу) у вигляді статистичних оцінок його параметрів. Процес моделювання економічної системи зводиться до машинної імітації досліджуваного процесу, котрий моделюється на ЕОМ з усіма суттєвими невизначеностями, випадковостями і породженим ними ризиком. |
Метод Монте-Карло широко використовується у всіх випадках імітації на ЕОМ. На сьогодні він охоплює будь-яку техніку статистичного здійснення вибірки, яке використовується для приблизних рішень кількісних проблем. | Метод Монте-Карло широко використовується у всіх випадках імітації на ЕОМ. На сьогодні він охоплює будь-яку техніку статистичного здійснення вибірки, яке використовується для приблизних рішень кількісних проблем. | ||
| − | Він | + | Він застосовується: |
Для визначення площі довільних фігур. | Для визначення площі довільних фігур. | ||
| Рядок 182: | Рядок 186: | ||
Для моделювання поведінки складних екологічних та економічних систем. | Для моделювання поведінки складних екологічних та економічних систем. | ||
| − | Розв’язування задач методом статистичного моделювання полягає в | + | Розв’язування задач методом статистичного моделювання полягає в: |
* Опрацювання й побудова структурної схеми процесу, виявлення основних взаємозв’язків; | * Опрацювання й побудова структурної схеми процесу, виявлення основних взаємозв’язків; | ||
| Рядок 198: | Рядок 202: | ||
Оскільки випадкові події й випадкові функції можуть подаватися з використанням випадкових величин, то й моделювання випадкових подій і випадкових функцій проводиться за допомогою випадкових величин. | Оскільки випадкові події й випадкові функції можуть подаватися з використанням випадкових величин, то й моделювання випадкових подій і випадкових функцій проводиться за допомогою випадкових величин. | ||
| − | Імітаційна модель — логіко-математичний опис об'єкту, який може бути використаний для експериментування на комп'ютері в цілях проектування, аналізу і оцінки функціонування об'єкту. Імітаційне моделювання — це окремий випадок математичного моделювання, метод дослідження, заснований на тому, що система, яка вивчається, замінюється імітатором і з ним проводяться експерименти з метою отримання інформації про цю систему | + | Імітаційна модель — логіко-математичний опис об'єкту, який може бути використаний для експериментування на комп'ютері в цілях проектування, аналізу і оцінки функціонування об'єкту. Імітаційне моделювання — це окремий випадок математичного моделювання, метод дослідження, заснований на тому, що система, яка вивчається, замінюється імітатором і з ним проводяться експерименти з метою отримання інформації про цю систему. |
== Література == | == Література == | ||
Поточна версія на 07:55, 27 травня 2013
Метод Монте-Карло (за назвою міста, яке відоме своїми гральними домами) — загальна назва групи числових методів, заснованих на одержанні великої кількості реалізацій стохастичного (випадкового) процесу, який формується у той спосіб, щоб його імовірнісні характеристики збыгалися з аналогічними величинами задачі, яка вирішується. Використовується для вирішення задач у фізиці, математиці, економіці, оптимізації, теорії управління тощо.
Метод Монте-Карло — це метод імітації для приблизного відтворення реальних явищ. Він об'єднує аналіз чутливості (сприйнятливості) і аналіз розподілювання ймовірностей вхідних змінних. Цей метод дає змогу побудувати модель, мінімізуючи дані, а також максимізувати значення даних, які використовуються в моделі. Побудова моделі починається з визначення функціональних залежностей у реальній системі. Після чого можна одержати кількісне рішення, використовуючи теорію ймовірності й таблиці випадкових чисел.
Огляд
Не існує єдиного методу Монте-Карло, цей термін описує великий і широко використовуваний клас підходів. Проте ці підходи використовують в своїй основі єдиний шаблон:
1. Визначити область можливих вхідних даних.
2. Випадковим чином згенерувати вхідні дані із визначеної вище області за допомогою деякого заданого розподілу ймовірностей.
3. Виконати детерміновані обчислення над вхідними даними.
4. Проміжні результати окремих розрахунків звести у кінцевий результат.
Наприклад, значення π можна наблизити використанням методу Монте-Карло:
1. Намалюйте квадрат на підлозі, а потім вмалюйте коло всередину нього. З геометрії, співвідношення площі вписаною кола до площі зовнішнього квадрата становить π / 4.
2. Рівномірно розкидати деякі об'єкти однакового розміру по всій площі квадрата. Наприклад, це можуть бути зерна рису.
3. Оскільки дві області знаходяться в співвідношенні π / 4 , об'єкти повинні потрапити в області приблизно в тій же пропорції. Таким чином, підрахувавши кількість об'єктів в колі і розділити на загальну кількість об'єктів в квадраті, отримаємо наближене значення π / 4.
4. Помноживши результат на 4, отримаємо наближене значення власне самого π.
Зміст
Історія
Алгоритм Буффона для визначення числа Пі
Випадкові величини використовувалися для вирішення різних прикладних завдань достатньо давно. Прикладом може служити спосіб визначення числа Пі, який був запропонований Буффоном ще в 1777 році. Суть методу була в киданні голки довжиною L на площину, розкреслену паралельними прямими, розташованими на відстані r один від одного (див. Рис. 1). Вірогідність (як видно з подальшого контексту, йдеться не про вірогідність, а про математичне чекання кількості перетинів за один дослід; вірогідністю це стає лише за умови, що L) того, що відрізок пересіче пряму, пов'язана з числом Пі:де
- A — відстань від початку голки до найближчої до неї прямої;
- O — кут голки відносно прямих.
Цей інтеграл легко взяти: (при умові, що r > L) тому підрахувавши долю відрізків, що пересікають прямі, можна приблизно визначити це число. При збільшенні кількості спроб точність отримуваного результату збільшуватиметься.
У 1864 році капітан Фокс, видужуючи після поранення, щоб якось зайняти себе, реалізував експеримент по киданню голки. Результати представлені в таблиці:
| Число кидків | Число пересічень | Довжина голки | Відстань між прямими | Обертання | Значення Пі | |
|---|---|---|---|---|---|---|
| Перша спроба | 500 | 236 | 3 | 4 | Відсутня | 3,1780 |
| Друга спроба | 530 | 253 | 3 | 4 | Присутня | 3,1423 |
| Третя спроба | 590 | 939 | 5 | 2 | Присутня | 3,1416 |
Коментарі:
- Обертання плоскості застосовувалося (і як показують результати — успішно) для того, щоб зменшити систематичну помилку.
- У третій спробі довжина голки була більше за відстань між лініями, що дозволило не збільшуючи числа кидань ефективно збільшити число подій і підвищити точність.
Зв'язок стохастичних процесів і диференціальних рівнянь
Створення математичного апарату стохастичних методів почалося в кінці 19-го століття. У 1899 році лорд Релей показав, що одновимірне випадкове блукання на безкінечних гратах може давати наближене вирішення параболічного диференціального рівняння. Андрій Колмогоров в 1931 році дав великий поштовх розвитку стохастичних підходів до вирішення різних математичних завдань, оскільки він зумів довести, що ланцюги Маркова пов'язані з деякими інтегро-дифференціальними рівняннями. У 1933 році Іван Петровський показав, що випадкове блукання, створююче Марківський ланцюг, асимптотика пов'язане з вирішенням еліптичного диференціального рівняння в частинних похідних. Після цих відкриттів стало зрозуміло, що стохастичні процеси можна описувати диференціальними рівняннями і, відповідно, досліджувати при допомозі добре на той момент розроблених математичних методів вирішення цих рівнянь.
Народження методу Монте-Карло в Лос-Аламосі
Спочатку Енріко Фермі в 1930-х роках в Італії, а потім Джон фон Нейман і Станіслав Улам в 1940-х в Лос-Аламосі передбачили, що можна використовувати зв'язок між стохастичними процесами і диференціальними рівняннями «у зворотний бік». Вони запропонували використовувати стохастичний підхід для апроксимації багатовимірних інтегралів в рівняннях перенесення, що виникли у зв'язку із завданням про рух нейтрона в ізотропному середовищі.
Ідея була розвинена Уламом, який, за іронією долі, також, як і Фокс, боровся з вимушеним неробством під час одужання після хвороби, і, розкладаючи пасьянси, задався питанням, яка вірогідність того, що пасьянс «складеться». Йому в голову прийшла ідея, що замість того, щоб використовувати звичайні для подібних завдань міркування комбінаторики, можна просто поставити «експеримент» велике число разів і, таким чином, підрахувавши число вдалих результатів, оцінити їх вірогідність. Він же запропонував використовувати комп'ютери для розрахунків методом Монте-Карло.
Поява перших електронних комп'ютерів, які могли з великою швидкістю генерувати псевдовипадкові числа, різко розширила круг завдань, для вирішення яких стохастичний підхід виявився ефективнішим, ніж інші математичні методи. Після цього стався великий прорив, і метод Монте-Карло застосовувався в багатьох завданнях, проте його використання не завжди було виправдане через велику кількість обчислень, необхідних для здобуття відповіді із заданою точністю.
Роком народження методу Монте-Карло вважається 1949 рік, коли в світ виходить стаття Метрополіса і Улама «Метод Монте-Карло». Назва методу походить від назви міста в князівстві Монако, широко відомого своїми багаточисельними казино, оскільки саме рулетка є одним з найвідоміших генераторів випадкових чисел. Станіслав Улам пише в своїй автобіографії «Пригоди математика», що назва була запропонована Ніколасом Метрополісом на честь його дядька, який був азартним гравцем.
Подальший розвиток і сучасність
У 1950-х роках метод використовувався для розрахунків при розробці водневої бомби. Основні заслуги в розвитку методу в цей час належать співробітникам лабораторій ВПС США і корпорації RAND.
У 1970-х роках в нової області математики — теорії обчислювальної складності було показано, що існує клас завдань, складність (кількість обчислень, необхідних для здобуття точної відповіді) яких зростає з розмірністю завдання експоненціально. Інколи можна, пожертвувавши точністю, знайти алгоритм, складність якого зростає повільніше, але є велика кількість завдань, для якої цього не можна зробити (наприклад, завдання визначення об'єму опуклого тіла в 'n'-мірному евклідовому просторі) і метод Монте-Карло є єдиною можливістю для здобуття досить точної відповіді за прийнятний час. В даний час основні зусилля дослідників направлені на створення ефективних Монте-Карло алгоритмів різних фізичних, хімічних і соціальних процесів для паралельних обчислювальних систем.
Інтегрування методом Монте-Карло
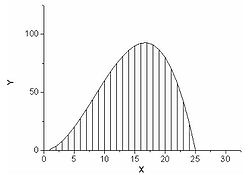
Припустимо, необхідно взяти інтеграл від деякої функції. Скористаємося неформальним геометричним описом інтеграла і розумітимемо його як площа під графіком цієї функції.
Для визначення цієї площі можна скористатися одним із звичайних чисельних методів інтеграції: розбити відрізок на підвідрізки, підрахувати площу під графіком функції на кожному з них і скласти. Передбачимо, що для функції, представленої на малюнку 2, досить розбиття на 25 відрізків і, отже, обчислення 25 значень функції. Представимо тепер, ми маємо справу з n-мірною функцією. Тоді нам необхідно 25^n відрізків і стільки ж обчислень значення функції. При розмірності функції більше 10 завдання стає величезним. Оскільки простори великої розмірності зустрічаються, зокрема, в завданнях теорії струн, а також багатьох інших фізичних завданнях, де є системи з багатьма мірами свободи, необхідно мати метод рішення,який би не настільки сильно залежав від розмірності. Саме такою властивістю володіє метод Монте-Карло.
Звичайний алгоритм Монте-Карло інтегрування
Для визначення площі під графіком функції можна використовувати наступний стохастичний алгоритм:
- обмежимо функцію прямокутником (n-вимірнім паралелепіпедом в разі багатьох вимірів), площу якого S(par) можна легко обчислити;
- «накидаємо» в цей прямокутник (паралелепіпед) деяку кількість точок N штук), координати яких вибиратимемо випадковим чином;
- визначимо число точок (K штук), які попадуть під графік функції;
- площа області, обмеженою функцією і осями координат, S дається
Для малого числа вимірів інтегрованої функції продуктивність Монте-Карло інтеграції набагато нижча, ніж продуктивність детермінованих методів. Проте, в деяких випадках, коли функція задана неявно, а необхідно визначити область, задану у вигляді складних нерівностей, стохастичний метод може виявитися переважнішим.
Використання вибірки за значимістю
Очевидно, що точність обчислень можна збільшити, якщо область, що обмежує шукану функцію, буде максимальна до неї наближена. Для цього необхідно використовувати випадкові величини з розподілом, форма якого максимально близька до форми інтегрованої функції. На цьому заснований один з методів поліпшення збіжності в обчисленнях методом Монте-Карло: вибірка за значимістю.
Оптимізація
Застосування в фізіці
Комп'ютерне моделювання грає в сучасній фізиці важливу роль і метод Монте-Карло є одним з найпоширеніших в багатьох областях від квантової фізики до фізики твердого тіла, фізики плазми і астрофізики.
Алгоритм Метрополіса
Традиційно метод Монте-Карло застосовувався для визначення різних фізичних параметрів систем, що знаходяться в стані термодинамічної рівноваги. Припустимо є набір W(S) можливих станів фізичної системи S. Для визначення середнього значення деякої величини A необхідно розрахувати
, где підсумовування виробляється по тих, що всім складаються S з W(S), P(S) — вірогідність стану S.
Динамічне (кінетичне) формулювання
Пряме моделювання методом Монте-Карло
Пряме моделювання методом Монте-Карло якого-небудь фізичного процесу має на увазі моделювання поведінки окремих елементарних частин фізичної системи. По суті це пряме моделювання близьке до рішення задачі з перших принципів, проте зазвичай для прискорення розрахунків допускається вживання яких-небудь фізичних наближень. Прикладом можуть служити розрахунки різних процесів методом молекулярної динаміки: з одного боку система описується через поведінку її елементарних складених частин, з іншого боку, використовуваний потенціал взаємодії частенько є емпіричним.
Приклади прямого моделювання методом Монте-Карло:
- Моделювання опромінення твердих тіл іонами в наближенні бінарних зіткнень.
- Пряме Монте-Карло моделювання розріджених газів.
- Більшість кінетичних Монте-Карло моделей належать до прямих (зокрема, дослідження молекулярно-пучкової епітакси).
Квантовий метод Монте-Карло
Квантовий метод Монте-Карло широко застосовується для дослідження складних молекул і твердих тіл. Цю назву об'єднує декілька різних методів. Перший з них це варіаційний метод Монте-Карло, яке по суті є чисельною інтеграцією багатовимірних інтегралів, що виникають при вирішенні рівняння Шредінгера. Для вирішення завдання, в якому бере участь 1000 електронів, необхідне узяття 3000-мірних інтегралів, і при вирішенні таких завдань метод Монте-Карло має величезну перевагу в продуктивності у порівнянні з іншими чисельними методами інтеграції. Інший різновид методу Монте-Карло — це дифузійний метод Монте-Карло, який, втім, не дуже раціональний.
Імітаційне моделювання
Існує клас об'єктів, для яких з різних причин не розроблені аналітичні моделі або не розроблені методи розв'язування задач про такі моделі. В цьому випадку математична модель замінюється імітатором або імітаційною моделлю.
Поняття імітаційної моделі
Імітаційна модель — логіко-математичний опис об'єкту, який може бути використаний для експериментування на комп'ютері в цілях проектування, аналізу і оцінки функціонування об'єкту. Імітаційне моделювання — це окремий випадок математичного моделювання, метод дослідження, заснований на тому, що система, яка вивчається, замінюється імітатором і з ним проводяться експерименти з метою отримання інформації про цю систему. Експериментування з імітатором називають імітацією (імітація — це збагнення суті явища, не вдаючись до експериментів на реальному об'єкті).
Імітаційне моделювання
Імітаційне моделювання (машинна імітація) - особлива форма проведення експериментів на ЕОМ з математичними моделями, які з певним ступенем ймовірності описують закономірності функціонування реальних систем і об’єктів. Це метод, що дозволяє будувати моделі процесів, що описують, як ці процеси проходили б насправді. Таку модель можна «програти» в часі як для одного випробування, так і заданої їх кількості. При цьому результати визначатимуться випадковим характером процесів. За цими даними можна отримати достатньо стійку статистику. Імітація як метод розв'язування нетривіальних задач отримала початковий розвиток у зв'язку із створенням ЕОМ в 1950х — 1960х роках. Імітаційні (алгоритмічні) моделі можуть бути детермінованими і стохастичними. В останньому випадку за допомогою датчиків (генераторів) випадкових чисел імітується вплив (дія) невизначених і випадкових чинників. Такий метод імітаційного моде¬лювання дістав назву методу статистичного моделювання (статистичних прогонів, чи методу Монте-Карло). На даний час цей метод вважають одним із найефективніших методів дослідження складних систем, а часто і єдиним практично доступним методом отримання нової інформації щодо поведінки гіпотетичної системи (на етапі її проектування).
Винахідником методу Монте-Карло називають Станіслава Улама (Stanislaw Ulam), американського математика, який народився у м. Львові. С.Улам перш за все відомий як людина, яка брала участь в проектуванні водневої бомби з Едуардом Теллером на початку 50-х років. Під час II Світової Війни Станіслав Марцин Улам і Джон фон Нейман (Neumann) працювали в Лос-Аламосі на Манхеттенському Проекті над моделюванням нейтронної дифузії в розщеплюваному матеріалі. Метод Монте-Карло він винайшов в 1946 р., коли одужуючи після хвороби, і, розкладаючи пасьянси, задався питанням, яка вірогідність того, що пасьянс «складеться». Йому в голову прийшла ідея, що замість того, щоб використовувати звичайні для подібних завдань міркування комбінаторики, можна просто поставити «експеримент» велике число раз і, таким чином, підрахувавши число вдалих результатів, оцінити їх вірогідність. Він же запропонував використовувати комп'ютери для розрахунків методом Монте-Карло. Працюючи з Джоном фон Нейманом і Ніколасом Метрополісом (N. Metropolis), він розвивав алгоритми для комп'ютерних виконань, також як і досліджував засіб перетворення не випадкових проблем у випадкові форми, які полегшили б їх розв’язок через статистичне здійснення вибірки. Ця робота перетворила статистичне здійснення вибірки з математичної цікавості на формальну методологію, що застосовується до широкого кола різноманітних проблем. Поява перших електронних комп'ютерів, які могли з великою швидкістю генерувати псевдовипадкові числа, різко розширила круг завдань, для вирішення яких стохастичний підхід виявився ефективнішим, ніж інші математичні методи. Після цього відбувся великий прорив і метод Монте-Карло застосовувався в багатьох завданнях, проте його використання не завжди було виправдано через велику кількість обчислень, необхідних для отримання відповіді із заданою точністю.
Метод Монте-Карло — це сукупність формальних процедур, засобами яких відтворюються на ЕОМ будь-які випадкові фактори (випадкові події, випадкові величини з довільним розподілом, випадкові вектори тощо). У межах цього підходу будується ймовірнісна модель, яка відповідає математичній чи фізичній задачі, і на ній реалізується випадкова вибірка. «Розігрування» вибірок за методом Монте-Карло є основним принципом імітаційного моделювання систем із стохастичними (випадковими, імовірними) елементами. Метод Монте-Карло — це метод імітації для приблизного відтворення реальних явищ. Він об'єднує аналіз чутливості (сприйнятливості) і аналіз розподілювання ймовірностей вхідних змінних. Цей метод дає змогу побудувати модель, мінімізуючи дані, а також максимізувати значення даних, які використовуються в моделі. Побудова моделі починається з визначення функціональних залежностей у реальній системі. Після чого можна одержати кількісне рішення, використовуючи теорію ймовірності й таблиці випадкових чисел. [2, стр.70] Метод статистичного моделювання (чи метод Монте-Карло) — це спосіб дослідження невизначених (стохастичних) економічних об’єктів і процесів, коли не повністю (до певної міри) є відомими внутрішні взаємодії в цих системах. Цей метод полягає у модельному відтворенні процесу за допомогою стохастичної математичної моделі та обчисленні характеристик цього процесу. Одне таке відтворення можливого (випадкового) стану функціонування модельованої системи називають реалізацією (чи імітаційним прогоном).Після кожного прогону реєструють сукупність параметрів, що характеризують випадкову подію (її реалізацію). Метод ґрунтується на багатократних прогонах (випадкових реалізаціях) на підставі побудованої моделі з подальшим статистичним опрацюванням отриманих даних з метою визначення числових характеристик досліджуваного об’єкта (процесу) у вигляді статистичних оцінок його параметрів. Процес моделювання економічної системи зводиться до машинної імітації досліджуваного процесу, котрий моделюється на ЕОМ з усіма суттєвими невизначеностями, випадковостями і породженим ними ризиком.
Метод Монте-Карло широко використовується у всіх випадках імітації на ЕОМ. На сьогодні він охоплює будь-яку техніку статистичного здійснення вибірки, яке використовується для приблизних рішень кількісних проблем. Він застосовується:
Для визначення площі довільних фігур.
Для вибору найкращих стратегій в задачах, де присутні багато випадкових факторів.
Для визначення ймовірності, чи відбудеться якась подія.
Для побудови різних геометричних об”єктів, в тому числі лабіринтів та фракталів.
Для моделювання поведінки складних екологічних та економічних систем.
Розв’язування задач методом статистичного моделювання полягає в:
- Опрацювання й побудова структурної схеми процесу, виявлення основних взаємозв’язків;
- Формалізований опис процесу;
- Моделювання випадкових явищ (випадкових подій, випадкових величин, випадкових функцій), що притаманні досліджуваній системі;
- Моделювання процесу функціонування системи (на підставі використання даних, що отримані на попередньому етапі) — відтворення процесу відповідно до розробленої структурної схеми і формалізованого опису (імітаційні прогони);
- Накопичення результатів моделювання (імітаційних прогонів), статистичне опрацювання, аналіз та інтерпретація їх.
Будь-які твердження стосовно характеристик модельованої системи повинні ґрунтуватися на результатах відповідних перевірок за допомогою методів математичної статистики.
Оскільки випадкові події й випадкові функції можуть подаватися з використанням випадкових величин, то й моделювання випадкових подій і випадкових функцій проводиться за допомогою випадкових величин.
Імітаційна модель — логіко-математичний опис об'єкту, який може бути використаний для експериментування на комп'ютері в цілях проектування, аналізу і оцінки функціонування об'єкту. Імітаційне моделювання — це окремий випадок математичного моделювання, метод дослідження, заснований на тому, що система, яка вивчається, замінюється імітатором і з ним проводяться експерименти з метою отримання інформації про цю систему.
Література
Микитюк П.П. Інноваційний менеджмент: Навчальний посібник. – Тернопіль: Економічна думка, 2006. – 295 с.
http://znaimo.com.ua/Метод_Монте-Карло
Літнарович Р.М. Побудова і дослідження істинної моделі якості засвоєння базової дисципліни. Апроксимація поліномом першого степеня.. МЕГУ, Рівне, 2009, –32с.
Літнарович Р.М. Основи математики. Дослідження результатів психолого-педагогічного експерименту експоненціальною функцією. Частина 4. МЕГУ, Рівне, 2006, –17с.
Літнарович Р.М. Дослідження точності апроксимації результатів психолого-педагогічного експерименту методом статистичних випробувань Монте Карло.Ч.1.МЕГУ, Рівне,2006,-45с.