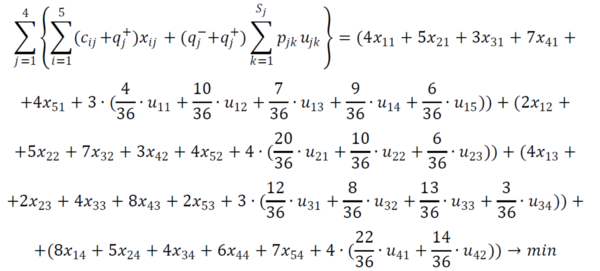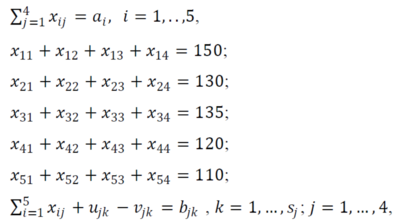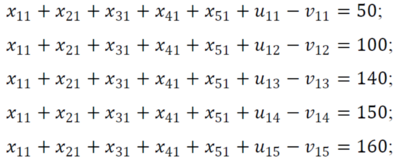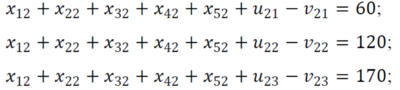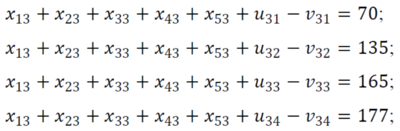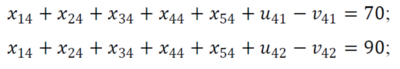Відмінності між версіями «Стохастична транспортна задача. Дискретний розподіл попиту.»
(Створена сторінка: Нехай тепер попит <math>\ b_j(w) </math> розподілений дискретно. В цьому випадку детермінований ек...) |
4625918 (обговорення • внесок) |
||
| (не показані 9 проміжних версій 2 учасників) | |||
| Рядок 1: | Рядок 1: | ||
| − | + | Транспортна задача — задача про оптимальний план перевезення продуктів із пунктів відправлення до пунктів споживання за умови, що витрати на перевезення будуть мінімальними. | |
| + | |||
| + | Стохастична транспортна задача – задача про оптимальний план перевезення продуктів із пунктів відправлення до пунктів споживання за умови, що витрати на перевезення будуть мінімальними та попит на продукцію буде випадковим. | ||
| + | |||
| + | Розглянемо тепер попит <math>\ b_j(w) </math> розподілений дискретно. В цьому випадку детермінований еквівалент стохастичної транспортної задачі виявляється задачею лінійного програмування. | ||
Припустимо, що попит <math>\ b_j </math> в j-му пункті споживані приймає значення <math>\ b_{jk} </math> з ймовірностями <math>\ p_{jk} </math> <math>\ (k=1,...,s_j) </math>. Нехай <math>\ q^{(-)}_j </math> і <math>\ q^{(+)}_j </math> - штраф за дефіцит і витрати зберігання одиниці продукту. | Припустимо, що попит <math>\ b_j </math> в j-му пункті споживані приймає значення <math>\ b_{jk} </math> з ймовірностями <math>\ p_{jk} </math> <math>\ (k=1,...,s_j) </math>. Нехай <math>\ q^{(-)}_j </math> і <math>\ q^{(+)}_j </math> - штраф за дефіцит і витрати зберігання одиниці продукту. | ||
| Рядок 7: | Рядок 11: | ||
Цільова функція стохастичної транспортної задачі – математичне сподівання сумарних витрат – записується у вигляді | Цільова функція стохастичної транспортної задачі – математичне сподівання сумарних витрат – записується у вигляді | ||
<math>\ \sum^{n}_{j=1} \left \{\sum^{m}_{i=1} {c_{ij}x_{ij}} + q^{(-)}_j \sum^{s_j}_{k=1} {p_{jk}u_{jk}} + q^{(+)}_j \sum^{s_j}_{k=1} {p_{jk}v_{jk}} \right \}</math> | <math>\ \sum^{n}_{j=1} \left \{\sum^{m}_{i=1} {c_{ij}x_{ij}} + q^{(-)}_j \sum^{s_j}_{k=1} {p_{jk}u_{jk}} + q^{(+)}_j \sum^{s_j}_{k=1} {p_{jk}v_{jk}} \right \}</math> | ||
| + | Завжди має місце рівність <math> \sum^{m}_{i=1} {x_{ij}+u_{jk}-v_{jk}} = b_{jk} </math>, <math>\ k=1,...,s_{j} </math> ; <math>\ j=1,...,n </math>. | ||
| + | Обчислюючи <math>\ v_{jk} </math> із останньої рівності, перепишемо вираз для цільового функціонала задачі | ||
| + | <math>\ \sum^{n}_{j=1} \left \{\sum^{m}_{i=1} {(c_{ij} + q^{(+)}_j)x_{ij}} +(q^{(-)}_j+q^{(+)}_j) \sum^{s_j}_{k=1} {p_{jk}u_{jk}} \right \} - \sum^{n}_{j=1} {q^{(+)}_j \bar{b}_j} </math> | ||
| + | |||
| + | Де <math> \bar{b}_j = Mb_j(w)= \sum^{s_j}_{k=1} {p_{jk}b_{jk}} </math>. Останній член в виразі для критерію якості розв’язку стохастичної транспортної задачі не містить параметрів управління. Тому в формальній моделі задачі його можна опустити. | ||
| + | Таким чином, детермінований еквівалент стохастичної транспортної задачі з дискретним розподілом попиту може бути представлений наступною моделлю лінійного програмування: | ||
| + | |||
| + | <math>\ \sum^{n}_{j=1} \left \{\sum^{m}_{i=1} {(c_{ij} + q^{(+)}_{ij})x_{j}} +(q^{(-)}_{ij}+q^{(+)}_{ij}) \sum^{s_j}_{k=1} {p_{jk}u_{jk}} \right \} \rightarrow min </math> , | ||
| + | |||
| + | <math> \sum^{n}_{j=1} {x_{ij}=a_i} </math>, <math>\ i=1,...,m </math> | ||
| + | |||
| + | <math> \sum^{m}_{i=1} {x_{ij}+u_{jk}-v_{jk}} = b_{jk} </math> , <math>\ k=1,...,s_j </math>; <math>\ j=1,...,n </math> | ||
| + | |||
| + | <math> \sum^{n}_{j=1} \sum^{s_j}_{k=1} {(v_{jk}-u_{jk})} = \sum^{m}_{i=1} {a_i} - \sum^{n}_{j=1} \sum^{s_j}_{k=1} {b_jk} </math> | ||
| + | |||
| + | <math>\ x_{ij} \geq 0 </math>, <math>\ u_{jk} \geq 0 </math>, <math>\ v_{jk} \geq 0 </math>, <math>\ i=1,...,m </math>, <math>\ k=1,...,s_j </math>, <math>\ j=1,...,n </math>. | ||
| + | |||
| + | Приклад побудови детермінованого еквівалента стохастичної транспортної задачі з дискретно розподіленим попитом | ||
| + | |||
| + | Нехай ми маємо 5 пунктів постачальників цегли в різних містах: Київ, Донецьк, Харків, Одеса, Вінниця зі своїми обсягами товару відповідно (150;130;135;120;110). Ми маємо 4 підприємства в м. Кропивницький, які потребують поставки товару: «Епіцентр», «Агрохімресурс», «Креатив», «Червона Зірка». Матриця цін перевезень цегли від постачальників до споживачів така: | ||
| + | [[Файл:Рис1.png|200px]] | ||
| + | Попит у кожного споживача стохастичний. Також вводяться значення штрафів за надлишок а також недостачу товару [[Файл:рис2.png|100px]] та [[Файл:рис3.png|100px]] відповідно. | ||
| + | Ми маємо статистичні дані по кожному з підприємств споживачів по замовленню цегли за останні три роки. | ||
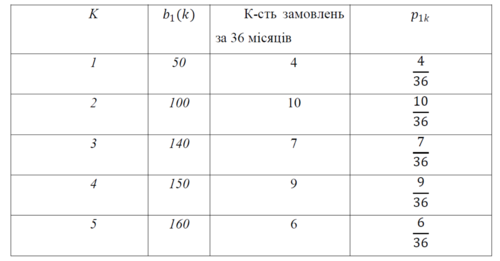
| + | Запишемо таблицю попиту для першого підприємства «Епіцентр»: | ||
| + | Таблиця попиту для першого підприємства | ||
| + | [[Файл:Table1.png|500px]] | ||
| + | |||
| + | Запишемо таблицю попиту для другого підприємства «Агрохімресурс»: | ||
| + | Таблиця попиту для другого підприємства <br> | ||
| + | [[Файл:Ttable2.png|500px]] | ||
| + | |||
| + | Запишемо таблицю попиту для третього підприємства «Креатив»: | ||
| + | Таблиця попиту для третього підприємства <br> | ||
| + | [[Файл:Table3.png|500px]] | ||
| + | |||
| + | Запишемо таблицю попиту для четвертого підприємства «Червона Зірка»: | ||
| + | Таблиця попиту для четвертого підприємства<br> | ||
| + | [[Файл:Table4.png|500px]]<br> | ||
| + | |||
| + | Відмітимо, що 𝑥<sub>''ij''</sub> – обсяг перевезень з А<sub>''i''</sub>-го пункта в B<sub>''j''</sub>-ому споживачу.<br> | ||
| + | Введемо допоміжні змінні u<sub>''jk''</sub> та v<sub>''jk''</sub> – обсяг дефіциту та надлишку.<br> | ||
| + | Запишемо цільову функцію [[Файл:Рис4.jpg|500px]]<br> | ||
| + | Доцільна рівність [[Файл:Рис5.png|500px]]<br> | ||
| + | Виразивши v<sub>''jk''</sub> з останньої рівності та підставивши цей вираз у цільову функцію отримаємо: [[Файл:Рис6.png|400px]]<br> | ||
| + | |||
| + | Розпишемо її детальніше<br> | ||
| + | [[Файл:Рис7.png|600px]]<br> | ||
| + | |||
| + | Та маємо обмеження<br> | ||
| + | [[Файл:Рис8.png|400px]]<br> | ||
| + | |||
| + | Обмеження для 1-го замовника<br> | ||
| + | [[Файл:Рис9.png|400px]]<br> | ||
| + | |||
| + | Обмеження для 2-го замовника<br> | ||
| + | [[Файл:Рис10.png|400px]]<br> | ||
| + | |||
| + | Обмеження для 3-го замовника<br> | ||
| + | [[Файл:Рис11.png|400px]]<br> | ||
| + | |||
| + | Обмеження для 4-го замовника<br> | ||
| + | [[Файл:Рис12.png|400px]]<br> | ||
| + | <p><big><i>x<sub>ij</sub>≥0, u<sub>jk</sub>≥0, i = 1, ..., 5; k = 1, ..., s<sub>j</sub>; j = 1, ..., 4.</i></big></p> | ||
| + | Отже ми отримали модель лінійного програмування, яка містить 48 змінних. | ||
| + | |||
| + | |||
| + | |||
| + | Виконала: [[Користувач:Лисенко Наталія Дмитрівна|Лисенко Наталія Дмитрівна ]] | ||
| + | |||
| + | Доповнювала: [[Користувач:4625918|Андреєва Ольга]] | ||
Поточна версія на 12:39, 13 травня 2020
Транспортна задача — задача про оптимальний план перевезення продуктів із пунктів відправлення до пунктів споживання за умови, що витрати на перевезення будуть мінімальними.
Стохастична транспортна задача – задача про оптимальний план перевезення продуктів із пунктів відправлення до пунктів споживання за умови, що витрати на перевезення будуть мінімальними та попит на продукцію буде випадковим.
Розглянемо тепер попит Неможливо розібрати вираз (невідома помилка): \ b_j(w)
розподілений дискретно. В цьому випадку детермінований еквівалент стохастичної транспортної задачі виявляється задачею лінійного програмування.
Припустимо, що попит Неможливо розібрати вираз (невідома помилка): \ b_j
в j-му пункті споживані приймає значення Неможливо розібрати вираз (невідома помилка): \ b_{jk}
з ймовірностями Неможливо розібрати вираз (невідома помилка): \ p_{jk}
Неможливо розібрати вираз (невідома помилка): \ (k=1,...,s_j)
. Нехай Неможливо розібрати вираз (невідома помилка): \ q^{(-)}_j
і Неможливо розібрати вираз (невідома помилка): \ q^{(+)}_j
- штраф за дефіцит і витрати зберігання одиниці продукту.
Введемо допоміжні зміні Неможливо розібрати вираз (невідома помилка): \ u_{jk}
і Неможливо розібрати вираз (невідома помилка): \ v_{jk}
, рівні відповідні величини дефіциту (і надлишкового продукту) в j-м пункті споживання при реалізації k-го варіанту попиту, тобто при Неможливо розібрати вираз (невідома помилка): \ b_j=b_{jk} .
Цільова функція стохастичної транспортної задачі – математичне сподівання сумарних витрат – записується у вигляді Неможливо розібрати вираз (невідома помилка): \ \sum^{n}_{j=1} \left \{\sum^{m}_{i=1} {c_{ij}x_{ij}} + q^{(-)}_j \sum^{s_j}_{k=1} {p_{jk}u_{jk}} + q^{(+)}_j \sum^{s_j}_{k=1} {p_{jk}v_{jk}} \right \}
Завжди має місце рівність Неможливо розібрати вираз (невідома помилка): \sum^{m}_{i=1} {x_{ij}+u_{jk}-v_{jk}} = b_{jk} , Неможливо розібрати вираз (невідома помилка): \ k=1,...,s_{j}
; Неможливо розібрати вираз (невідома помилка): \ j=1,...,n
. Обчислюючи Неможливо розібрати вираз (невідома помилка): \ v_{jk}
із останньої рівності, перепишемо вираз для цільового функціонала задачі
Неможливо розібрати вираз (невідома помилка): \ \sum^{n}_{j=1} \left \{\sum^{m}_{i=1} {(c_{ij} + q^{(+)}_j)x_{ij}} +(q^{(-)}_j+q^{(+)}_j) \sum^{s_j}_{k=1} {p_{jk}u_{jk}} \right \} - \sum^{n}_{j=1} {q^{(+)}_j \bar{b}_j}
Де Неможливо розібрати вираз (невідома помилка): \bar{b}_j = Mb_j(w)= \sum^{s_j}_{k=1} {p_{jk}b_{jk}}
. Останній член в виразі для критерію якості розв’язку стохастичної транспортної задачі не містить параметрів управління. Тому в формальній моделі задачі його можна опустити.
Таким чином, детермінований еквівалент стохастичної транспортної задачі з дискретним розподілом попиту може бути представлений наступною моделлю лінійного програмування:
Неможливо розібрати вираз (невідома помилка): \ \sum^{n}_{j=1} \left \{\sum^{m}_{i=1} {(c_{ij} + q^{(+)}_{ij})x_{j}} +(q^{(-)}_{ij}+q^{(+)}_{ij}) \sum^{s_j}_{k=1} {p_{jk}u_{jk}} \right \} \rightarrow min
,
Неможливо розібрати вираз (невідома помилка): \sum^{n}_{j=1} {x_{ij}=a_i} , Неможливо розібрати вираз (невідома помилка): \ i=1,...,m
Неможливо розібрати вираз (невідома помилка): \sum^{m}_{i=1} {x_{ij}+u_{jk}-v_{jk}} = b_{jk}
, Неможливо розібрати вираз (невідома помилка): \ k=1,...,s_j
- Неможливо розібрати вираз (невідома помилка): \ j=1,...,n
Неможливо розібрати вираз (невідома помилка): \sum^{n}_{j=1} \sum^{s_j}_{k=1} {(v_{jk}-u_{jk})} = \sum^{m}_{i=1} {a_i} - \sum^{n}_{j=1} \sum^{s_j}_{k=1} {b_jk}
Неможливо розібрати вираз (невідома помилка): \ x_{ij} \geq 0
, Неможливо розібрати вираз (невідома помилка): \ u_{jk} \geq 0
, Неможливо розібрати вираз (невідома помилка): \ v_{jk} \geq 0
, Неможливо розібрати вираз (невідома помилка): \ i=1,...,m
, Неможливо розібрати вираз (невідома помилка): \ k=1,...,s_j
, Неможливо розібрати вираз (невідома помилка): \ j=1,...,n
.
Приклад побудови детермінованого еквівалента стохастичної транспортної задачі з дискретно розподіленим попитом
Нехай ми маємо 5 пунктів постачальників цегли в різних містах: Київ, Донецьк, Харків, Одеса, Вінниця зі своїми обсягами товару відповідно (150;130;135;120;110). Ми маємо 4 підприємства в м. Кропивницький, які потребують поставки товару: «Епіцентр», «Агрохімресурс», «Креатив», «Червона Зірка». Матриця цін перевезень цегли від постачальників до споживачів така:
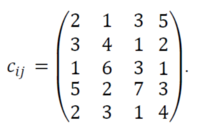 Попит у кожного споживача стохастичний. Також вводяться значення штрафів за надлишок а також недостачу товару
Попит у кожного споживача стохастичний. Також вводяться значення штрафів за надлишок а також недостачу товару ![]() та
та ![]() відповідно.
Ми маємо статистичні дані по кожному з підприємств споживачів по замовленню цегли за останні три роки.
Запишемо таблицю попиту для першого підприємства «Епіцентр»:
Таблиця попиту для першого підприємства
відповідно.
Ми маємо статистичні дані по кожному з підприємств споживачів по замовленню цегли за останні три роки.
Запишемо таблицю попиту для першого підприємства «Епіцентр»:
Таблиця попиту для першого підприємства
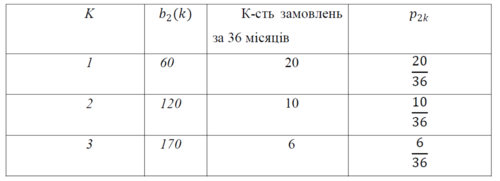
Запишемо таблицю попиту для другого підприємства «Агрохімресурс»:
Таблиця попиту для другого підприємства
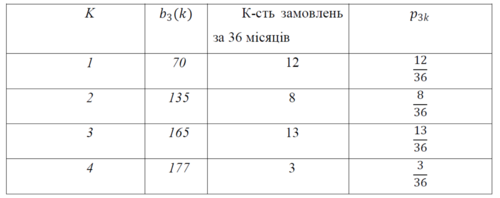
Запишемо таблицю попиту для третього підприємства «Креатив»:
Таблиця попиту для третього підприємства
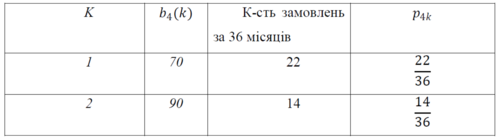
Запишемо таблицю попиту для четвертого підприємства «Червона Зірка»:
Таблиця попиту для четвертого підприємства
Відмітимо, що 𝑥ij – обсяг перевезень з Аi-го пункта в Bj-ому споживачу.
Введемо допоміжні змінні ujk та vjk – обсяг дефіциту та надлишку.
Запишемо цільову функцію ![]()
Доцільна рівність ![]()
Виразивши vjk з останньої рівності та підставивши цей вираз у цільову функцію отримаємо: 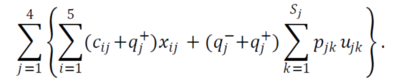
xij≥0, ujk≥0, i = 1, ..., 5; k = 1, ..., sj; j = 1, ..., 4.
Отже ми отримали модель лінійного програмування, яка містить 48 змінних.
Виконала: Лисенко Наталія Дмитрівна
Доповнювала: Андреєва Ольга