Відмінності між версіями «Класифікація квазілінійних систем»
Tenatin (обговорення • внесок) (Створена сторінка: Поняття характеристик дозволяє класифікувати рівняння математичної фізики. Розглянемо ...) |
Tenatin (обговорення • внесок) |
||
| (не показано 9 проміжних версій цього учасника) | |||
| Рядок 1: | Рядок 1: | ||
| − | Поняття характеристик дозволяє класифікувати рівняння математичної фізики. Розглянемо систему рівнянь у приватних похідних першого порядку, символічно представимо у вигляді | + | Поняття характеристик дозволяє класифікувати рівняння математичної фізики. Розглянемо систему рівнянь у приватних похідних першого порядку, символічно представимо у вигляді<br> |
| − | + | [[Файл:Tenatin1.PNG]] | |
| − | Тут u і f є n-мірні вектори невідомих і відомих функцій відповідно; С - матриця коефіцієнтів, що залежать від x, t. Ця система - майже лінійна. Систему (1) зведемо до одного рівняння n-го порядку і n-1 зв'язкам. Поставимо задачу відшукання умов розв'язності задачі Коші поблизу кривої g в площині x, t. Для знаходженням перших похідних поблизу цієї кривої систему (1) слід доповнити рівняннями | + | Тут u і f є n-мірні вектори невідомих і відомих функцій відповідно; С - матриця коефіцієнтів, що залежать від x, t. Ця система - майже лінійна. Систему (1) зведемо до одного рівняння n-го порядку і n-1 зв'язкам. Поставимо задачу відшукання умов розв'язності задачі Коші поблизу кривої g в площині x, t. Для знаходженням перших похідних поблизу цієї кривої систему (1) слід доповнити рівняннями <br> |
| − | + | [[Файл:Tenatin2.PNG]] | |
| − | Розв'язність цього завдання пов'язана з визначником | + | Розв'язність цього завдання пов'язана з визначником <br> |
| − | + | [[Файл:Tenatin3.PNG]] | |
Тому характеристиками є криві, що задовольняють рівнянням dx / dt = k (x, t), в яких поля коефіцієнтів локального нахилу характеристик k (x, t), очевидно. Суть власні числа матриці С. Спектр похідної матриці з дійсними коефіцієнтами в загальному випадку є підмножина комплексних чисел. Якщо спектр дійсний і простий у будь-якій точці даної області, то система (1) називаеться (5)гіперболічною. Якщо спектр комплексний (звичайно, якщо n парне), то система – (6)еліптична. В інших випадках будови спектра система називається параболічної. Таким чином, тільки гіперболічні системи мають інваріантну систему координат, що складається з характеристик. | Тому характеристиками є криві, що задовольняють рівнянням dx / dt = k (x, t), в яких поля коефіцієнтів локального нахилу характеристик k (x, t), очевидно. Суть власні числа матриці С. Спектр похідної матриці з дійсними коефіцієнтами в загальному випадку є підмножина комплексних чисел. Якщо спектр дійсний і простий у будь-якій точці даної області, то система (1) називаеться (5)гіперболічною. Якщо спектр комплексний (звичайно, якщо n парне), то система – (6)еліптична. В інших випадках будови спектра система називається параболічної. Таким чином, тільки гіперболічні системи мають інваріантну систему координат, що складається з характеристик. | ||
| − | + | Слово "інваріантний" означає зв'язаність з самим рівнянням, а не з його конкретним записом в тій чи іншій системі координат. Для таких систем має сенс завдання Коші у відкритій області, узгодженої з розташуванням поля характеристик, і не мають сенсу постановки в обмежених областях. Гіперболічні системи описують поширення збурень з кінцевою швидкістю. Для еліптичних систем характеристики відсутні, і мають сенс тільки завдання на замкнутої області (хай і нескінченної), а умови на кордоні називаютя крайовими. Збурення граничних умов поширюються цими системами миттєво ("дифузійним механізмом"). (7)Приклад еліптичної системи - рівняння Лапласа | |
| − | + | Для цього рівняння другого порядку розрізняють задачу Діріхле (на кордоні задано значення функції), завдання Неймана (на кордоні задана похідна по нормалі до кордону) і змішану задачу. Параболічні системи, що мають поле характеристик, не утворить систему координат, допускають постановки в відкритій області, узгодженої з розташуванням характеристик. Тобто крайові ("початково-граничні") завдання для параболічних систем можуть мати сенс, а можуть і не мати його. (8)Наприклад, рівняння дифузії (теплопровідності) з умовами, заданими в області описує розподіл субстанції v по простору: початкові особливості з часом згладжуються. Але якщо поставити завдання на області з спочатку гладкого профілю протягом зворотного ходу часу неминуче будуть виникати особливості, тобто вирішення такого завдання будуть нестійкими. Завдання, в яких потрібно встановити "минуле" по справжньому, відносяться до некоректних по Адамара завданням. Коректність по Адамара означає існування, єдиність і стійкість рішення (в даному випадку по відношенню до обурення початкових умов). Причина таких властивостей параболічного рівняння дифузії криється в його неінваріантни по відношенню до заміни. | |
Класифікація систем з використанням характеристик обощаются на квазілінійних системи (тобто системи диференціальних рівнянь, лінійні відносно старших похідних, але містять в коефіцієнтах шукані функції та їх похідні нижчих порядків) і на системи з числом незалежних змінних більше двох (тоді характеристики є вже поверхнями) . Досліджуємо, наприклад, систему (1) є квазілінійної, вважаючи початкові "обурення" кінцевими. | Класифікація систем з використанням характеристик обощаются на квазілінійних системи (тобто системи диференціальних рівнянь, лінійні відносно старших похідних, але містять в коефіцієнтах шукані функції та їх похідні нижчих порядків) і на системи з числом незалежних змінних більше двох (тоді характеристики є вже поверхнями) . Досліджуємо, наприклад, систему (1) є квазілінійної, вважаючи початкові "обурення" кінцевими. | ||
| − | Введенням функції тиску | + | Введенням функції тиску [[Файл:Tenatin4.PNG]] ця система зводиться до наступного:<br> |
| − | + | [[Файл:Снимок5.PNG]] | |
| − | За зразком, даному для квазілінійних систем (додаючи до незалежних змінних v), або елементарними складанням і відніманням рівнянь отримуємо: | + | За зразком, даному для квазілінійних систем (додаючи до незалежних змінних v), або елементарними складанням і відніманням рівнянь отримуємо:<br> |
| − | + | [[Файл:Tenatin6.PNG]] | |
| − | Очевидно, характеристиками системи будуть криві (12) | + | Очевидно, характеристиками системи будуть криві (12)[[Файл:Tenatin7.PNG]] , на яких постійні відповідні величини (картинка) Тут на відміну від системи, яка описує малі обурення, а являє собою поле місцевої швидкості звуку, [[Файл:Tenatin8.PNG]] -- відносні швидкості поширення хвиль по газу. Уздовж першого сімейства характеристик поширюється хвиля розрідження, вздовж другого - хвиля стиснення. |
| + | == Література == | ||
| + | 1. Моисеев Н. Н< Элементы теории оптимальных систем. М.: Наука, 1975. <br> | ||
| + | 2. Первозванский А. А., Гайцгори В. Г. Декомпозиция, агрегирование и приближен- • | ||
| + | нал оптимизация. М.: Наука, 1979.<br> | ||
| + | 3;. Черноуськб Ф. Л., Колмановский В. Б. Вычислительные и приближенные методы | ||
| + | оптимального управления // Матем. анализ. (Итоги науки и техн.) М.: ВИНИТИ,, | ||
| + | . 1977. Т. 14. С. 101-166.<br> | ||
| + | 4. Альбрехт Э. Г. Об управлении движением нелинейных систем//Дйффёренц. | ||
| + | ур-ния. 1966. Т. 2. № 3. С. 324-334. <br> | ||
Поточна версія на 09:40, 18 травня 2012
Поняття характеристик дозволяє класифікувати рівняння математичної фізики. Розглянемо систему рівнянь у приватних похідних першого порядку, символічно представимо у вигляді
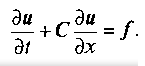
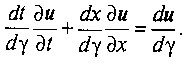
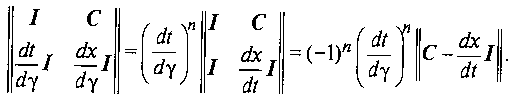
ця система зводиться до наступного:
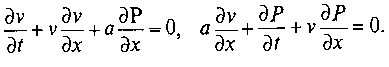
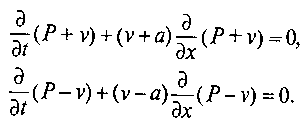
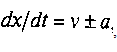
-- відносні швидкості поширення хвиль по газу. Уздовж першого сімейства характеристик поширюється хвиля розрідження, вздовж другого - хвиля стиснення.
Література
1. Моисеев Н. Н< Элементы теории оптимальных систем. М.: Наука, 1975.
2. Первозванский А. А., Гайцгори В. Г. Декомпозиция, агрегирование и приближен- •
нал оптимизация. М.: Наука, 1979.
3;. Черноуськб Ф. Л., Колмановский В. Б. Вычислительные и приближенные методы
оптимального управления // Матем. анализ. (Итоги науки и техн.) М.: ВИНИТИ,,
. 1977. Т. 14. С. 101-166.
4. Альбрехт Э. Г. Об управлении движением нелинейных систем//Дйффёренц.
ур-ния. 1966. Т. 2. № 3. С. 324-334.
