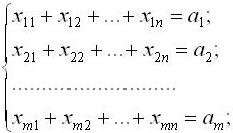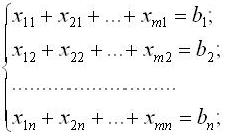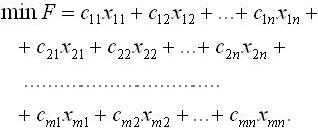Відмінності між версіями «Економічна і математична постановка ТЗ.»
| (не показані 34 проміжні версії цього учасника) | |||
| Рядок 1: | Рядок 1: | ||
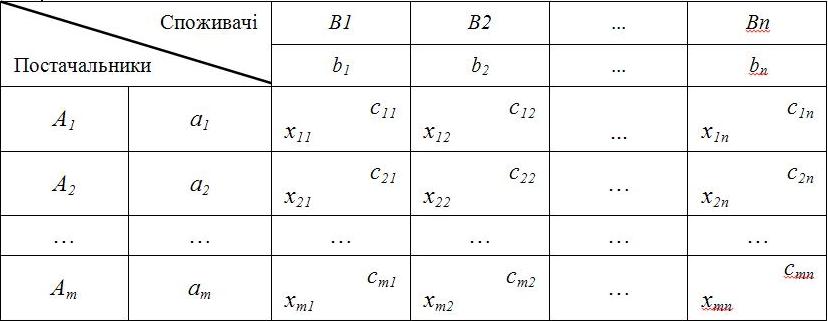
| − | Класична транспортна задача лінійного програмування фор-мулюється так: деякий однорідний продукт, що знаходиться у m постачальників | + | Класична транспортна задача лінійного програмування фор-мулюється так: деякий однорідний продукт, що знаходиться у m постачальників <math>A_{i}</math> в обсягах <math>a_{1} ,a_{2} ,...,a_{m}</math> одиниць відповідно необ-хідно перевезти n споживачам <math>B_{j}</math> в обсягах <math>b_{1} ,b_{2} ,...,b_{n}</math> одиниць. При цьому виконується умова, що загальний наявний обсяг про-дукції у постачальників дорівнює загальному попиту всіх спожи-вачів. Відомі вартості <math>C_{ij}</math> перевезень одиниці продукції від кож-ного <math>A_{i}</math>-го постачальника до кожного <math>B_{j}</math>-го споживача, що подані як елементи матриці виду: |
| + | [[Файл:Безымяннывй.JPG]] | ||
| + | |||
| + | Необхідно визначити план перевезень, за якого вся продукція була б вивезена від постачальників, повністю задоволені потреби споживачів і загальна вартість всіх перевезень була б мінімаль-ною. | ||
| + | У такій постановці задачі ефективність плану перевезень ви-значається його вартістю і така задача має назву транспортної задачі за критерієм вартості перевезень. | ||
| + | |||
| + | Позначимо через <math>x_{ij}</math> обсяг продукції, що перевозиться від <math>A_{i}</math> постачальника до <math>B_{j}</math> споживача <math>(i=\overline {1,m} ;\,\,j=\overline {1,n} )</math> | ||
| + | |||
| + | [[Файл:Безымянwqный.JPG]] | ||
| + | |||
| + | Мають виконуватися такі умови: | ||
| + | |||
| + | 1) сумарний обсяг продукції, що вивозиться з кожного і-го пункту, має дорівнювати запасу продукції в даному пункті: | ||
| + | |||
| + | [[Файл:Безымянsddfsfный.JPG]] | ||
| + | |||
| + | 2) сумарний обсяг продукції, що ввезений кожному j-му спо-живачеві, має дорівнювати його потребам: | ||
| + | |||
| + | [[Файл:Копия Безымяwнsddfsfный.JPG]] | ||
| + | |||
| + | 3) сумарна вартість всіх перевезень повинна бути мінімаль-ною: | ||
| + | |||
| + | [[Файл:Безымянныйddddd.JPG]] | ||
| + | |||
| + | |||
| + | Очевидно, що <math>x_{ij} \ge 0,\,\;\,i=\overline {1,m} ;\;\,\,j=\overline {1,n}</math> | ||
| + | |||
| + | У скороченій формі запису математична модель транспортної за-дачі за критерієм вартості перевезень має такий вигляд: | ||
| + | |||
| + | <math>\min F=\sum\limits_{i=1}^m {\sum\limits_{j=1}^n {c_{ij} x_{ij} } }</math> (1) | ||
| + | |||
| + | за обмежень: | ||
| + | |||
| + | <math>\sum\limits_{j=1}^n {x_{ij} =a_{i} } \,\,\,\left( {i=\overline {1,m} } | ||
| + | \right) | ||
| + | </math> (2) | ||
| + | |||
| + | <math>\sum\limits_{j=1}^n {x_{ij} =b_{j} } \,\,\,\left( {i=\overline {1,n} } | ||
| + | \right) | ||
| + | </math> (3) | ||
| + | |||
| + | <math>x_{ij} \ge 0\,\,\,\,\left( {i=\overline {1,m} ;\,\,\,j=\overline {1,n} } | ||
| + | \right) | ||
| + | </math> (4) | ||
| + | |||
| + | У розглянутій задачі має виконуватися умова: | ||
| + | |||
| + | <math>\sum\limits_{i=1}^m {a_{i} } =\sum\limits_{j=1}^n {b_{j} }</math> (5) | ||
| + | |||
| + | Транспортну задачу називають збалансованою, або закри-тою, якщо виконується умова (5). Якщо ж така умова не вико-нується, то транспортну задачу називають незбалансованою, або відкритою. | ||
| + | |||
| + | Домовимося планом транспортної задачі називати будь-який невід’ємний розв’язок системи обмежень (2)—(4), який позначають матрицею <math>X=x_{ij}</math> <math>\left( {i=\overline {1,m} ;\,\,\,j=\overline {1,n} } \right)</math>. Значення невідомих величин <math>x_{ij}</math> — обсяги продукції, що мають бути перевезені від i-х постачальників до j-х споживачів, називатимемо перевезеннями. | ||
| + | |||
| + | Оптимальним планом транспортної задачі називають матри-цю <math>X^{\ast }=x_{ij}^{\ast }</math> <math>\left( {i=\overline {1,m} ;\,\,\,j=\overline {1,n} } \right)</math>, яка задовольняє умови задачі, і для якої цільова функція (1) набирає найменшого значення. | ||
Поточна версія на 15:08, 16 травня 2012
Класична транспортна задача лінійного програмування фор-мулюється так: деякий однорідний продукт, що знаходиться у m постачальників Неможливо розібрати вираз (невідома помилка): A_{i}
в обсягах Неможливо розібрати вираз (невідома помилка): a_{1} ,a_{2} ,...,a_{m}
одиниць відповідно необ-хідно перевезти n споживачам Неможливо розібрати вираз (невідома помилка): B_{j}
в обсягах Неможливо розібрати вираз (невідома помилка): b_{1} ,b_{2} ,...,b_{n}
одиниць. При цьому виконується умова, що загальний наявний обсяг про-дукції у постачальників дорівнює загальному попиту всіх спожи-вачів. Відомі вартості Неможливо розібрати вираз (невідома помилка): C_{ij}
перевезень одиниці продукції від кож-ного Неможливо розібрати вираз (невідома помилка): A_{i}
-го постачальника до кожного Неможливо розібрати вираз (невідома помилка): B_{j}
-го споживача, що подані як елементи матриці виду:
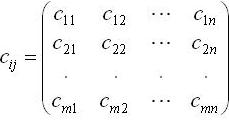
Необхідно визначити план перевезень, за якого вся продукція була б вивезена від постачальників, повністю задоволені потреби споживачів і загальна вартість всіх перевезень була б мінімаль-ною. У такій постановці задачі ефективність плану перевезень ви-значається його вартістю і така задача має назву транспортної задачі за критерієм вартості перевезень.
Позначимо через Неможливо розібрати вираз (невідома помилка): x_{ij}
обсяг продукції, що перевозиться від Неможливо розібрати вираз (невідома помилка): A_{i}
постачальника до Неможливо розібрати вираз (невідома помилка): B_{j}
споживача Неможливо розібрати вираз (невідома помилка): (i=\overline {1,m} ;\,\,j=\overline {1,n} )
Мають виконуватися такі умови:
1) сумарний обсяг продукції, що вивозиться з кожного і-го пункту, має дорівнювати запасу продукції в даному пункті:
2) сумарний обсяг продукції, що ввезений кожному j-му спо-живачеві, має дорівнювати його потребам:
3) сумарна вартість всіх перевезень повинна бути мінімаль-ною:
Очевидно, що Неможливо розібрати вираз (невідома помилка): x_{ij} \ge 0,\,\;\,i=\overline {1,m} ;\;\,\,j=\overline {1,n}
У скороченій формі запису математична модель транспортної за-дачі за критерієм вартості перевезень має такий вигляд:
Неможливо розібрати вираз (невідома помилка): \min F=\sum\limits_{i=1}^m {\sum\limits_{j=1}^n {c_{ij} x_{ij} } }
(1)
за обмежень:
Неможливо розібрати вираз (невідома помилка): \sum\limits_{j=1}^n {x_{ij} =a_{i} } \,\,\,\left( {i=\overline {1,m} } \right)
(2)
Неможливо розібрати вираз (невідома помилка): \sum\limits_{j=1}^n {x_{ij} =b_{j} } \,\,\,\left( {i=\overline {1,n} } \right)
(3)
Неможливо розібрати вираз (невідома помилка): x_{ij} \ge 0\,\,\,\,\left( {i=\overline {1,m} ;\,\,\,j=\overline {1,n} } \right)
(4)
У розглянутій задачі має виконуватися умова:
Неможливо розібрати вираз (невідома помилка): \sum\limits_{i=1}^m {a_{i} } =\sum\limits_{j=1}^n {b_{j} }
(5)
Транспортну задачу називають збалансованою, або закри-тою, якщо виконується умова (5). Якщо ж така умова не вико-нується, то транспортну задачу називають незбалансованою, або відкритою.
Домовимося планом транспортної задачі називати будь-який невід’ємний розв’язок системи обмежень (2)—(4), який позначають матрицею Неможливо розібрати вираз (невідома помилка): X=x_{ij}
Неможливо розібрати вираз (невідома помилка): \left( {i=\overline {1,m} ;\,\,\,j=\overline {1,n} } \right)
. Значення невідомих величин Неможливо розібрати вираз (невідома помилка): x_{ij}
— обсяги продукції, що мають бути перевезені від i-х постачальників до j-х споживачів, називатимемо перевезеннями.
Оптимальним планом транспортної задачі називають матри-цю Неможливо розібрати вираз (невідома помилка): X^{\ast }=x_{ij}^{\ast }
Неможливо розібрати вираз (невідома помилка): \left( {i=\overline {1,m} ;\,\,\,j=\overline {1,n} } \right)
, яка задовольняє умови задачі, і для якої цільова функція (1) набирає найменшого значення.