Відмінності між версіями «Критерії опорного плану.»

Матеріал з Вікі ЦДУ
Перейти до: навігація, пошук
(→‎Теорема)
(→‎Теорема)
 
(не показані 2 проміжні версії цього учасника)
Рядок 7: Рядок 7:
 
Вектори, що відповідають базисним клітинам, тобто базис-ним змінним, є лінійно незалежними, і потрібно довести ацик-лічність набору клітин, що відповідає будь-якій системі ліній-но незалежних векторів. Допустимо протилежне. Нехай деяка підсистема з даної системи базисних векторів утворює цикл, а саме:
 
Вектори, що відповідають базисним клітинам, тобто базис-ним змінним, є лінійно незалежними, і потрібно довести ацик-лічність набору клітин, що відповідає будь-якій системі ліній-но незалежних векторів. Допустимо протилежне. Нехай деяка підсистема з даної системи базисних векторів утворює цикл, а саме:
  
−
<math>(i_1,j_1); (i_1,j_2); (i_2,j_2) ;...; (i_k,j_k); (i_k,j_l)</math>(5.11)
+
<math>\ (i_1,j_1); (i_1,j_2); (i_2,j_2) ;...; (i_k,j_k); (i_k,j_l)</math>(5.11)
  
 
Складемо лінійну комбінацію таких векторів, що дорівнює нулю. Оскільки кожна змінна входить у систему обмежень лише двічі, то базисні вектори матимуть вид:
 
Складемо лінійну комбінацію таких векторів, що дорівнює нулю. Оскільки кожна змінна входить у систему обмежень лише двічі, то базисні вектори матимуть вид:
Рядок 23: Рядок 23:
 
Проте рівність (5.12) суперечить умові лінійної незалежності базисних векторів, отже, послідовність (5.11) є ациклічною.
 
Проте рівність (5.12) суперечить умові лінійної незалежності базисних векторів, отже, послідовність (5.11) є ациклічною.
 
Достатність. Нехай деякий план транспортної задачі є ацик¬лічним. Потрібно показати, що він є опорним планом, тобто до-вести лінійну незалежність векторів, що відповідають ненульо-вим компонентам плану.
 
Достатність. Нехай деякий план транспортної задачі є ацик¬лічним. Потрібно показати, що він є опорним планом, тобто до-вести лінійну незалежність векторів, що відповідають ненульо-вим компонентам плану.
 +
 
Всякий план не може містити від’ємних компонент, а кіль-кість лінійно незалежних між собою векторів у обмеженнях транспортної задачі завжди дорівнює m + n – 1, так що кількість відмінних від нуля компонент плану, якщо він опорний, не пере-вищує цієї величини.
 
Всякий план не може містити від’ємних компонент, а кіль-кість лінійно незалежних між собою векторів у обмеженнях транспортної задачі завжди дорівнює m + n – 1, так що кількість відмінних від нуля компонент плану, якщо він опорний, не пере-вищує цієї величини.
 
Позначимо множину всіх заповнених клітин через Н, а відпо-відні вектори —  . Доведемо достатність, міркуючи від супро-тивного. Нехай вектори  лінійно залежні. Розглянемо нульову лінійну комбінацію цих векторів:
 
Позначимо множину всіх заповнених клітин через Н, а відпо-відні вектори —  . Доведемо достатність, міркуючи від супро-тивного. Нехай вектори  лінійно залежні. Розглянемо нульову лінійну комбінацію цих векторів:
  
−
<math>\sum_{(i,j)\in H} \lambda_ij*a_{ij}{^*}</math>(5.13)
+
<math>\sum_{(i,j)\in H} \lambda_{ij}*a_{ij}{^*}</math>(5.13)
  
 
Деякі з коефіцієнтів  можуть відрізнятися від нуля. Нехай один з таких коефіцієнтів відповідає індексам <math> \ (i_1,j_1)</math> ,  тобто <math>\lambda_{i_1}{j_1}</math>. Тоді відповідний доданок у рівності (5.13) можна перенести в лі-ву частину рівняння:
 
Деякі з коефіцієнтів  можуть відрізнятися від нуля. Нехай один з таких коефіцієнтів відповідає індексам <math> \ (i_1,j_1)</math> ,  тобто <math>\lambda_{i_1}{j_1}</math>. Тоді відповідний доданок у рівності (5.13) можна перенести в лі-ву частину рівняння:
  
−
<math>- \lambda_{i_1}{j_1}*a_{i_1}{j_1}^* = \sum_{(i,j)\in H_1} \lambda_ij*a_ij^* </math>(5.14)
+
<math>- \lambda_{i_1}{j_1}*a_{i_1}{j_1}^* = \sum_{(i,j)\in H_1} \lambda_{ij}*a_{ij}{^*} </math>(5.14)
  
−
де <math>H_1=H-(i_1,j_1)</math>.
+
де <math>\ H_1=H-(i_1,j_1)</math>.
  
 
Оскільки і1-ша компонента в лівій частині (5.14) відмінна від нуля, то в правій частині також має бути хоча б один доданок з  
 
Оскільки і1-ша компонента в лівій частині (5.14) відмінна від нуля, то в правій частині також має бути хоча б один доданок з  
 
і-ою компонентою, що відмінна від нуля. Припустимо, що  . Відповідний доданок також можна перенести в ліву частину (5.14):
 
і-ою компонентою, що відмінна від нуля. Припустимо, що  . Відповідний доданок також можна перенести в ліву частину (5.14):
  
−
<math>- \lambda_{i_1}{j_1}*a_{i_1}{j_1}^* -\lambda_{i_1}{j_2}*a_{i_1}{j_2}^* = \sum_{(i,j)\in H_2} \lambda_ij*a_ij^*</math>(5.15)
+
<math>- \lambda_{i_1}{j_1}*a_{i_1}{j_1}^* -\lambda_{i_1}{j_2}*a_{i_1}{j_2}^* = \sum_{(i,j)\in H_2} \lambda_{ij}*a_{ij}{^*}</math>(5.15)
  
 
де <math>H_2=H_1-(i_1,j_1)</math>.  
 
де <math>H_2=H_1-(i_1,j_1)</math>.  
  
−
Оскільки <math>j_2 \ne j_1</math>  (інакше клітина (i_1,j_1  входила б у суму (5.13) двічі) і компонента m+j_2  лівої частини (5.15) відмінна від нуля, то серед доданків правої частини знайдеться хоча б один, для якого <math>\lambda_{i_2}{j_2} \ne 0</math> . Перенесемо його також в ліву частину рівняння. Отримаємо:
+
Оскільки <math>j_2 \ne j_1</math>  (інакше клітина (i_1,j_1  входила б у суму (5.13) двічі) і компонента m+j_2  лівої частини (5.15) відмінна від нуля, то серед доданків правої частини знайдеться хоча б один, для якого <math>\lambda_{i_2}{j_2} \ne 0</math>.
  
−
<math>- \lambda_{i_1}{j_1}*a_{i_1}{j_1}^* -\lambda_{i_1}{j_2}*a_{i_1}{j_2}^* -\lambda_{i_2}{j_2}*a_{i_2}{j_2}^*= \sum_{(i,j)\in H_3} \lambda_ij*a_ij^*</math>(5.16)
+
Перенесемо його також в ліву частину рівняння. Отримаємо:
 +
 
 +
<math>- \lambda_{i_1}{j_1}*a_{i_1}{j_1}^* -\lambda_{i_1}{j_2}*a_{i_1}{j_2}^* -\lambda_{i_2}{j_2}*a_{i_2}{j_2}^*= \sum_{(i,j)\in H_3} \lambda_{ij}*a_{ij}{^*}</math>(5.16)
  
 
де <math>H_3=H_2-(i_1,j_1)</math>.
 
де <math>H_3=H_2-(i_1,j_1)</math>.
 
Оскільки кількість заповнених клітин, що входять у множину Н, а отже, і кількість векторів a_ij^*  скінченна і не перевищує числа m*n =N, то через N кроків описаний процес перенесень обов’язково закінчиться.
 
Оскільки кількість заповнених клітин, що входять у множину Н, а отже, і кількість векторів a_ij^*  скінченна і не перевищує числа m*n =N, то через N кроків описаний процес перенесень обов’язково закінчиться.
 +
 
Після деякої непарної кількості кроків 2k-1  дістанемо рів-ність:
 
Після деякої непарної кількості кроків 2k-1  дістанемо рів-ність:
  
−
<math>- \sum_{p=1}^k \lambda_{i_p}{j_p}*a_{i_p}{j_p}^* - \sum_{p=1}^k-1 \lambda_{i_p}{j_{p+1}}*a_{i_p}{j_{p+1}}^* = \sum_{(i,j)\in H_{2*k-1}} \lambda_ij*a_ij^*</math>(5.17)
+
<math>- \sum_{p=1}^k \lambda_{i_p}{j_p}*a_{i_p}{j_p}^* - \sum_{p=1}^k-1 \lambda_{i_p}{j_{p+1}}*a_{i_p}{j_{p+1}}^* = \sum_{(i,j)\in H_{2*k-1}} \lambda_{ij}*a_{ij}{^*}</math>(5.17)
  
−
де H_{2*k-1}= H_{2*k-2}-(i_k,j_k) .
+
де <math>H_{2*k-1}= H_{2*k-2}-(i_k,j_k)</math> .
  
 
Якщо кількість кроків була парною, матимемо:
 
Якщо кількість кроків була парною, матимемо:
−
, (5.18)
+
 
−
де .
+
<math>- \sum_{p=1}^k \lambda_{i_p}{j_p}*a_{i_p}{j_p}^* - \sum_{p=1}^k \lambda_{i_p}{j_{p+1}}*a_{i_p}{j_{p+1}}^* = \sum_{(i,j)\in H_{2*k}} \lambda_{ij}*a_{ij}{^*}</math>(5.18)
−
Розглянемо співвідношення (5.17). При деякому значенні   серед доданків другої суми лівої частини знайдеться такий, що має індекс . Тоді всі клітини, що були перенесені в ліву частину після -го кроку, утворюють цикл.
+
 
 +
де <math>H_{2*k}= H_{2*k-1}-(i_k,j_k)</math>.
 +
 
 +
Розглянемо співвідношення (5.17). При деякому значенні <math> k(2\le k \le \frac{N}{2} </math>  серед доданків другої суми лівої частини знайдеться такий, що має індекс <math>i_w=i_k, 1 \le w \le k-1</math> . Тоді всі клітини, що були перенесені в ліву частину після (2w-1) -го кроку, утворюють цикл.
 +
 
 
Аналогічні міркування стосуються також (5.18).
 
Аналогічні міркування стосуються також (5.18).
−
Покажемо, що до закінчення процесу, виходячи з рівності (5.17), обов’язково матимемо цикл. Для цього припустимо, що . Тоді, згідно з попередніми міркуваннями, в правій частині (5.17) обов’язково знайдеться доданок з індексами , для якого , бо інакше б рівність (5.17) не справджувалась. Отже, процес перенесення у разі, якщо  , буде продовжува-тись. Проте, внаслідок згаданої скінченності процесу перенесень (N ≤ m • n) умова виконання рівностей (5.17) та (5.18) рівносиль-на тому, що випадок  обов’язково матиме місце, що означа-тиме побудову циклу.
+
Покажемо, що до закінчення процесу, виходячи з рівності (5.17), обов’язково матимемо цикл. Для цього припустимо, що <math>i_k \ne i_w</math> . Тоді, згідно з попередніми міркуваннями, в правій частині (5.17) обов’язково знайдеться доданок з індексами <math>\ (i_k,j_{k+1})</math>, для якого <math> \lambda_(i_k,j_{k+1}) \ne 0</math> , бо інакше б рівність (5.17) не справджувалась. Отже, процес перенесення у разі, якщо  <math>i_k \ne i_w</math>, буде продовжува-тись. Проте, внаслідок згаданої скінченності процесу перенесень (N ≤ m * n) умова виконання рівностей (5.17) та (5.18) рівносиль-на тому, що випадок  обов’язково матиме місце, що означа-тиме побудову циклу.
−
Отже, припущення лінійної залежності векторів , що описується рівнянням (5.13), означає, що серед відповідних клітин існує цикл, але це суперечить умові теореми. Значить, до-статність згаданої умови, а разом з тим і всю теорему доведено.
+
 
 +
Отже, припущення лінійної залежності векторів <math>a_{ij}{^*} \in H</math> , що описується рівнянням (5.13), означає, що серед відповідних клітин існує цикл, але це суперечить умові теореми. Значить, до-статність згаданої умови, а разом з тим і всю теорему доведено.
 +
 
 
Отже, базисні клітини опорного плану завжди утворюють ациклічну послідовність клітин.
 
Отже, базисні клітини опорного плану завжди утворюють ациклічну послідовність клітин.
 +
 +
== Література ==
 +
Наконечний С. І., Савіна С. С. Математичне програмування: Навч. посіб. - К.: КНЕУ, 2003. - 452 с.

Поточна версія на 10:37, 4 травня 2012

Теорема

Теорема 5.1. Щоб деякий план транспортної задачі був опор¬ним, необхідно і достатньо його ациклічності.

Доведення. Необхідність. Нехай у таблиці 5.1 міститься опор¬ний план транспортної задачі, тобто не більше ніж m + n – 1 клі-тин будуть заповненими. Якщо заповнених клітин менше, ніж m + n – 1, то решта базисних клітин знаходиться серед незапов-нених. Довести необхідність умови теореми означає довести ацикліч¬ність опорного плану. Вектори, що відповідають базисним клітинам, тобто базис-ним змінним, є лінійно незалежними, і потрібно довести ацик-лічність набору клітин, що відповідає будь-якій системі ліній-но незалежних векторів. Допустимо протилежне. Нехай деяка підсистема з даної системи базисних векторів утворює цикл, а саме:

Неможливо розібрати вираз (невідома помилка): \ (i_1,j_1); (i_1,j_2); (i_2,j_2) ;...; (i_k,j_k); (i_k,j_l) (5.11)

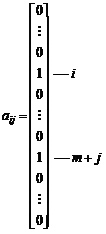
Складемо лінійну комбінацію таких векторів, що дорівнює нулю. Оскільки кожна змінна входить у систему обмежень лише двічі, то базисні вектори матимуть вид:

Vf.png

Лінійною комбінацією базисних векторів буде:

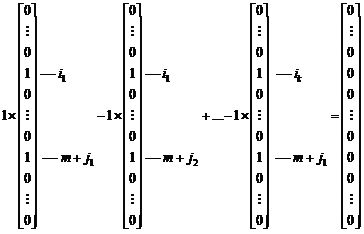
Bgf.png

Або

Неможливо розібрати вираз (невідома помилка): 1*a_{i_1}{j_1}-1*a_{i_1}{j_2}+1*a_{i_2}{j_2}- ... - 1*a_{i_k}{j_l}=0 (5.12)

Проте рівність (5.12) суперечить умові лінійної незалежності базисних векторів, отже, послідовність (5.11) є ациклічною. Достатність. Нехай деякий план транспортної задачі є ацик¬лічним. Потрібно показати, що він є опорним планом, тобто до-вести лінійну незалежність векторів, що відповідають ненульо-вим компонентам плану.

Всякий план не може містити від’ємних компонент, а кіль-кість лінійно незалежних між собою векторів у обмеженнях транспортної задачі завжди дорівнює m + n – 1, так що кількість відмінних від нуля компонент плану, якщо він опорний, не пере-вищує цієї величини. Позначимо множину всіх заповнених клітин через Н, а відпо-відні вектори — . Доведемо достатність, міркуючи від супро-тивного. Нехай вектори лінійно залежні. Розглянемо нульову лінійну комбінацію цих векторів:

Неможливо розібрати вираз (невідома помилка): \sum_{(i,j)\in H} \lambda_{ij}*a_{ij}{^*} (5.13)

Деякі з коефіцієнтів можуть відрізнятися від нуля. Нехай один з таких коефіцієнтів відповідає індексам Неможливо розібрати вираз (невідома помилка): \ (i_1,j_1) 

,  тобто Неможливо розібрати вираз (невідома помилка): \lambda_{i_1}{j_1}

. Тоді відповідний доданок у рівності (5.13) можна перенести в лі-ву частину рівняння:

Неможливо розібрати вираз (невідома помилка): - \lambda_{i_1}{j_1}*a_{i_1}{j_1}^* = \sum_{(i,j)\in H_1} \lambda_{ij}*a_{ij}{^*} (5.14)

де Неможливо розібрати вираз (невідома помилка): \ H_1=H-(i_1,j_1) .

Оскільки і1-ша компонента в лівій частині (5.14) відмінна від нуля, то в правій частині також має бути хоча б один доданок з і-ою компонентою, що відмінна від нуля. Припустимо, що . Відповідний доданок також можна перенести в ліву частину (5.14):

Неможливо розібрати вираз (невідома помилка): - \lambda_{i_1}{j_1}*a_{i_1}{j_1}^* -\lambda_{i_1}{j_2}*a_{i_1}{j_2}^* = \sum_{(i,j)\in H_2} \lambda_{ij}*a_{ij}{^*} (5.15)

де Неможливо розібрати вираз (невідома помилка): H_2=H_1-(i_1,j_1) .

Оскільки Неможливо розібрати вираз (невідома помилка): j_2 \ne j_1 

 (інакше клітина (i_1,j_1  входила б у суму (5.13) двічі) і компонента m+j_2  лівої частини (5.15) відмінна від нуля, то серед доданків правої частини знайдеться хоча б один, для якого Неможливо розібрати вираз (невідома помилка): \lambda_{i_2}{j_2} \ne 0

.

Перенесемо його також в ліву частину рівняння. Отримаємо:

Неможливо розібрати вираз (невідома помилка): - \lambda_{i_1}{j_1}*a_{i_1}{j_1}^* -\lambda_{i_1}{j_2}*a_{i_1}{j_2}^* -\lambda_{i_2}{j_2}*a_{i_2}{j_2}^*= \sum_{(i,j)\in H_3} \lambda_{ij}*a_{ij}{^*} (5.16)

де Неможливо розібрати вираз (невідома помилка): H_3=H_2-(i_1,j_1) . Оскільки кількість заповнених клітин, що входять у множину Н, а отже, і кількість векторів a_ij^* скінченна і не перевищує числа m*n =N, то через N кроків описаний процес перенесень обов’язково закінчиться.

Після деякої непарної кількості кроків 2k-1 дістанемо рів-ність:

Неможливо розібрати вираз (невідома помилка): - \sum_{p=1}^k \lambda_{i_p}{j_p}*a_{i_p}{j_p}^* - \sum_{p=1}^k-1 \lambda_{i_p}{j_{p+1}}*a_{i_p}{j_{p+1}}^* = \sum_{(i,j)\in H_{2*k-1}} \lambda_{ij}*a_{ij}{^*} (5.17)

де Неможливо розібрати вираз (невідома помилка): H_{2*k-1}= H_{2*k-2}-(i_k,j_k) 

.

Якщо кількість кроків була парною, матимемо:

Неможливо розібрати вираз (невідома помилка): - \sum_{p=1}^k \lambda_{i_p}{j_p}*a_{i_p}{j_p}^* - \sum_{p=1}^k \lambda_{i_p}{j_{p+1}}*a_{i_p}{j_{p+1}}^* = \sum_{(i,j)\in H_{2*k}} \lambda_{ij}*a_{ij}{^*} (5.18)

де Неможливо розібрати вираз (невідома помилка): H_{2*k}= H_{2*k-1}-(i_k,j_k) .

Розглянемо співвідношення (5.17). При деякому значенні Неможливо розібрати вираз (невідома помилка): k(2\le k \le \frac{N}{2} 

 серед доданків другої суми лівої частини знайдеться такий, що має індекс Неможливо розібрати вираз (невідома помилка): i_w=i_k, 1 \le w \le k-1
. Тоді всі клітини, що були перенесені в ліву частину після (2w-1) -го кроку, утворюють цикл.

Аналогічні міркування стосуються також (5.18). Покажемо, що до закінчення процесу, виходячи з рівності (5.17), обов’язково матимемо цикл. Для цього припустимо, що Неможливо розібрати вираз (невідома помилка): i_k \ne i_w 

. Тоді, згідно з попередніми міркуваннями, в правій частині (5.17) обов’язково знайдеться доданок з індексами Неможливо розібрати вираз (невідома помилка): \ (i_k,j_{k+1})

, для якого Неможливо розібрати вираз (невідома помилка): \lambda_(i_k,j_{k+1}) \ne 0 

, бо інакше б рівність (5.17) не справджувалась. Отже, процес перенесення у разі, якщо  Неможливо розібрати вираз (невідома помилка): i_k \ne i_w

, буде продовжува-тись. Проте, внаслідок згаданої скінченності процесу перенесень (N ≤ m * n) умова виконання рівностей (5.17) та (5.18) рівносиль-на тому, що випадок обов’язково матиме місце, що означа-тиме побудову циклу.

Отже, припущення лінійної залежності векторів Неможливо розібрати вираз (невідома помилка): a_{ij}{^*} \in H 

, що описується рівнянням (5.13), означає, що серед відповідних клітин існує цикл, але це суперечить умові теореми. Значить, до-статність згаданої умови, а разом з тим і всю теорему доведено.

Отже, базисні клітини опорного плану завжди утворюють ациклічну послідовність клітин.

Література

Наконечний С. І., Савіна С. С. Математичне програмування: Навч. посіб. - К.: КНЕУ, 2003. - 452 с.

Отримано з https://wiki.cusu.edu.ua/index.php?title=Критерії_опорного_плану.&oldid=66732