Відмінності між версіями «Золотий перетин»
Andrey (обговорення • внесок) |
|||
| (не показано 34 проміжні версії ще одного учасника) | |||
| Рядок 1: | Рядок 1: | ||
| − | Золотий перетин — це найкомфортніша для ока пропорція, форма, в основі побудови якої лежить поєднання симетрії і золотого перетину, сприяє якнайкращому зоровому сприйняттю і появі відчуття краси і гармонії. У математиці пропорцією називають рівність двох відносин: a : b = c : d. | + | '''Золотий перетин''' — це найкомфортніша для ока пропорція, форма, в основі побудови якої лежить поєднання симетрії і золотого перетину, сприяє якнайкращому зоровому сприйняттю і появі відчуття краси і гармонії. У математиці пропорцією називають рівність двох відносин: a : b = c : d. |
Відрізок прямої AB можна розділити точкою C на дві частини наступними способами: | Відрізок прямої AB можна розділити точкою C на дві частини наступними способами: | ||
| Рядок 11: | Рядок 11: | ||
Золотий перетин — це таке пропорційне ділення відрізка на нерівні частини, при якому весь відрізок так відноситься до більшої частини, як сама велика частина відноситься до меншої; або іншими словами, менший відрізок так відноситься до більшого, як більший до всього. | Золотий перетин — це таке пропорційне ділення відрізка на нерівні частини, при якому весь відрізок так відноситься до більшої частини, як сама велика частина відноситься до меншої; або іншими словами, менший відрізок так відноситься до більшого, як більший до всього. | ||
| − | а : b = b : c або c : b = b : а. | + | '''а : b = b : c або c : b = b : а.''' |
[[Image:Zs_p01.gif]] | [[Image:Zs_p01.gif]] | ||
| + | |||
| + | '''''Наприклад:'' a = 38,2, b = 62,8, c = 100, отже 38,2 : 62,8 = 62,8 : 100''' | ||
Відрізки золотої пропорції виражаються нескінченним ірраціональним дробом 0,618..., якщо c прийняти за одиницю, а = 0,382. Відношення ж відрізків а і b складає 1,618. Прямокутник з таким відношенням сторін стали називати золотим прямокутником. Він також володіє цікавими властивостями. Якщо від нього відрізати квадрат, то знову залишиться золотий прямокутник. Цей процес можна продовжувати до безкінечності. А якщо провести діагональ першого і другого прямокутника, то точка їх перетину належатиме всім золотим прямокутникам, які одержали. Є і золотий трикутник (рівнобедрений трикутник, у якого відношення довжини бічної сторони до довжини основи дорівнює 1,618), і золотий кубоїд (прямокутний паралелепіпед з ребрами, що мають довжини 1,618, 1 і 0,618). Золотий перетин не є штучним явищем. Воно дуже широко поширене в природі: золотий перетин можна знайти в пропорціях тіл багатьох рослин і тварин, а також морських раковин і пташиних яєць. | Відрізки золотої пропорції виражаються нескінченним ірраціональним дробом 0,618..., якщо c прийняти за одиницю, а = 0,382. Відношення ж відрізків а і b складає 1,618. Прямокутник з таким відношенням сторін стали називати золотим прямокутником. Він також володіє цікавими властивостями. Якщо від нього відрізати квадрат, то знову залишиться золотий прямокутник. Цей процес можна продовжувати до безкінечності. А якщо провести діагональ першого і другого прямокутника, то точка їх перетину належатиме всім золотим прямокутникам, які одержали. Є і золотий трикутник (рівнобедрений трикутник, у якого відношення довжини бічної сторони до довжини основи дорівнює 1,618), і золотий кубоїд (прямокутний паралелепіпед з ребрами, що мають довжини 1,618, 1 і 0,618). Золотий перетин не є штучним явищем. Воно дуже широко поширене в природі: золотий перетин можна знайти в пропорціях тіл багатьох рослин і тварин, а також морських раковин і пташиних яєць. | ||
| − | '''Приклад використання золотого перетину в рослинному світі. | + | '''Приклад використання золотого перетину в рослинному світі: цикорій.''' |
[[Image:Zs_p13.gif]] | [[Image:Zs_p13.gif]] | ||
| + | |||
| + | '''Приклад використання золотого перетину в тваринному світі: ящірка живородюча.''' | ||
| + | |||
| + | [[Image:Zs_p14.gif]] | ||
| + | |||
| + | '''Приклад використання золотого перетину в тваринному світі: пташине яйце.''' | ||
| + | |||
| + | [[Image:Zs_p15.gif]] | ||
| + | |||
Але найбільш вражаючий приклад "застосування" природою принципу золотого перетину — людське тіло. Воно цілком і його частини (обличчя, руки, грона рук і т. д.) наскрізь пронизані пропорцією 1,618. | Але найбільш вражаючий приклад "застосування" природою принципу золотого перетину — людське тіло. Воно цілком і його частини (обличчя, руки, грона рук і т. д.) наскрізь пронизані пропорцією 1,618. | ||
| + | |||
| + | '''Золоті пропорції в частинах тіла людини.''' | ||
| + | |||
| + | [[Image:Zs_p10.gif]] | ||
| + | |||
| + | '''Золоті пропорції в фігурі людини.''' | ||
| + | |||
| + | [[Image:Zs_p11.gif]] | ||
Принцип золотого перетину був відкритий людьми ще у глибокій старовині. Знамениті єгипетські піраміди в Гізі, наприклад, засновані на пропорціях золотого перетину. Молодші мексиканські піраміди і античний храм Парфенон також містять в собі пропорцію 1,618. | Принцип золотого перетину був відкритий людьми ще у глибокій старовині. Знамениті єгипетські піраміди в Гізі, наприклад, засновані на пропорціях золотого перетину. Молодші мексиканські піраміди і античний храм Парфенон також містять в собі пропорцію 1,618. | ||
| + | |||
| + | З золотим перетином пов'язано ім'я італійського математика Фібоначчі. Ряд чисел 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 і т.д. відомий як ряд Фібоначчі. Отримав він цей ряд, розмірковуючи на тему про те, скільки пар кроликів народиться від однієї пари (при місячній розгляді). Кожен член ряду, починаючи з третього, дорівнює сумі двох попередніх, а відношення суміжних чисел ряду наближається до відношенню золотого перетину (21 : 34 = 0,617; 34 : 55 = 0,618). Не зв'язуючи цей ряд із золотим перетином, Фібоначчі відкрив закономірність, до якої незмінно приходили всі дослідники золотого перетину в природі, мистецтві. | ||
З розвитком дизайну і технічної естетики дія закону золотого перетину розповсюдилася на конструювання машин, меблів і т.д. Проектування комп'ютерних інтерфейсів — не виключення. Форми діалогових вікон і елементів управління, сторони яких відносяться як 1,618, дуже привабливі для користувачів. Наприклад, дуже багато захоплень у користувачів програми Chameleon Clock (http://www.softshape.com) викликає така, здавалося б, буденна річ, як вид діалогового вікна Властивості. А все тому, що при його проектуванні використовувався саме принцип золотого перетину. | З розвитком дизайну і технічної естетики дія закону золотого перетину розповсюдилася на конструювання машин, меблів і т.д. Проектування комп'ютерних інтерфейсів — не виключення. Форми діалогових вікон і елементів управління, сторони яких відносяться як 1,618, дуже привабливі для користувачів. Наприклад, дуже багато захоплень у користувачів програми Chameleon Clock (http://www.softshape.com) викликає така, здавалося б, буденна річ, як вид діалогового вікна Властивості. А все тому, що при його проектуванні використовувався саме принцип золотого перетину. | ||
| + | |||
| + | ---- | ||
| + | Продемонструємо на невеличкому прикладі, як же застосовується золотий перетин в розробці інтерфейсів. | ||
| + | |||
| + | Припустимо, що ми працюємо в '''Delphi''', і нам потрібно привести до пропорцій золотого перетину діалогове вікно (і його елементи), в якому задаються параметри роботи для розробників програми. У вікні розташовані такі елементи: мітка ('''TLabel''') та рядок введення ('''TEdit'''), групбокс ('''TGroupBox''') з двома чекбоксами ('''TCheckBox''') та дві кнопки ('''TButton''') "'''OK'''", "'''Cancel'''". Після початкового компонування вікна отримуємо '''варіант 1 (рис.1)'''. | ||
| + | |||
| + | [[Image:2003230201.jpg]] | ||
| + | |||
| + | Оскільки значення має тільки вміст вікна, а розміри заголовка вікна можуть змінюватися у відповідності з настройками Windows, використовуємо розміри клієнтської частини вікна. Вони становлять 196х166 (ширина і висота). Розміри елементів управління - практично задаються по замовчуванню середовищем розробки. Їх розташування та коригування розмірів зараз нас не цікавлять. Наведемо до пропорції золотого перетину розміри клієнтської частини вікна виходячи зі співвідношення (висота / ширина) = 0,618. Для цього потрібно або зменшити його висоту або збільшити ширину. Оскільки зменшувати висоту нікуди, то збільшимо ширину, яка повинна дорівнювати (висота / 0,382) * 0,618 = 268. | ||
| + | |||
| + | А тепер, клієнтська частина вікна стала форматом 268х166. Тепер можна побудувати ряди Фібоначчі для двох напрямків - горизонталі і вертикалі, в порядку убування від (ширини / висоти) (зростання нам не потрібно). Кожний наступний елемент дорівнює попередньому, помноженому на 0,618. Для горизонталі - '''268, 166, 103, 64, 40, 25, 15, 9, 6, 3''', для вертикалі - '''166, 102, 63, 39, 24, 14, 6, 3'''. Видно, що вони практично однакові (з урахуванням округлення). Виходячи з цих рядів і будемо корегувати розміри і положення елементів керування у вікні. | ||
| + | |||
| + | Відразу можна помітити, що рядок введення та групбокс мають Left = 6, а мітка Top = 6, що відповідає одному з чисел ряду. Для Label цей параметр дорівнює 7, тому зрушимо позначку вліво на один піксель. Для Edit: Top = 24, що також відповідає одному з чисел ряду. Оскільки ми збільшили ширину вікна, то збільшимо і ширину Edit так, щоб відстань його правої частини становило 6 пікселів від правого краю вікна, точніше, від внутрішньої сторони його рамки (ширина буде 256). Аналогічно збільшимо по ширині і групбокс. | ||
| + | |||
| + | Змістивши кнопки до правого краю вікна (6 пікселів до рамки для кнопки "Cancel"), збільшивши відстань по горизонталі між ними з 5 до 6 пікселів. Відстань до нижньої межі вікна для кнопок (5 пікселів) також збільшимо на одиницю (до 6). | ||
| + | |||
| + | Піднімемо групбокс на 3 пікселі, щоб забезпечити відстань від його нижньої межі до кнопок у 6 пікселів. Чекбокси мають значення Left = 14, а відстань між ними - 9 пікселів, тому їх не міняємо ('''див. ряд'''). | ||
| + | |||
| + | У результаті всіх маніпуляцій отримуємо '''варіант 2 (рис. 2).''' | ||
| + | |||
| + | [[Image:2003230202.jpg]] | ||
| + | |||
| + | Порівнюючи початковий і підсумковий варіант, можна помітити, що вікно, що зображене на '''рис. 2''', виглядає набагато краще, хоча, на перший погляд, і сталося невиправдане збільшення розмірів деяких його елементів. | ||
| + | |||
| + | При проектуванні вікон програми існує певний мінімальний розмір, який потрібно витримувати між елементами (наприклад, для розглянутого випадку - 6 пікселів). Щоб полегшити роботу, можна використовувати налаштування '''Delphi''' "'''Grid size X'''", "'''Grid size X'''" при включеному чекбоксі "'''Snap to grid'''" у вікні "'''Environement options'''", вкладка "'''Preferences'''". Це не дозволить зробити відстані між елементами менше заданих мінімумів. | ||
| + | |||
| + | Потрібно відзначити, що приведення зовнішнього вигляду інтерфейсу до співвідношенням золотого перетину не повинно бути обов’язковим. Зловживати ним не варто, в усьому потрібна міра. Це бажана, але не завжди необхідна операція. Адже, крім золотого перетину, є й інші правила. Так що золоті пропорції вікон не повинні перекривати "золоті пропорції" логіки, послідовності і т.д. Головне - пізнання, і тоді правила не зроблять розробника своїм полоненим. | ||
| + | |||
| + | Аналогічним чином до пропорцій золотого перетину можна навести і зовнішній вигляд сторінок сайтів, принцип той же самий. | ||
| + | |||
| + | |||
---- | ---- | ||
[[category:РІС]] | [[category:РІС]] | ||
Поточна версія на 12:39, 24 грудня 2012
Золотий перетин — це найкомфортніша для ока пропорція, форма, в основі побудови якої лежить поєднання симетрії і золотого перетину, сприяє якнайкращому зоровому сприйняттю і появі відчуття краси і гармонії. У математиці пропорцією називають рівність двох відносин: a : b = c : d.
Відрізок прямої AB можна розділити точкою C на дві частини наступними способами:
- на дві рівні частини AB : АС = АВ : ВС,
- на дві нерівні частини в будь-якому відношенні (такі частини пропорції не утворюють): таким чином, коли АВ : ВС = ВС : АС.
Останнє і є золоте ділення або ділення відрізка в крайньому і середньому відношенні.
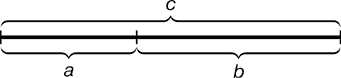
Золотий перетин — це таке пропорційне ділення відрізка на нерівні частини, при якому весь відрізок так відноситься до більшої частини, як сама велика частина відноситься до меншої; або іншими словами, менший відрізок так відноситься до більшого, як більший до всього.
а : b = b : c або c : b = b : а.
Наприклад: a = 38,2, b = 62,8, c = 100, отже 38,2 : 62,8 = 62,8 : 100
Відрізки золотої пропорції виражаються нескінченним ірраціональним дробом 0,618..., якщо c прийняти за одиницю, а = 0,382. Відношення ж відрізків а і b складає 1,618. Прямокутник з таким відношенням сторін стали називати золотим прямокутником. Він також володіє цікавими властивостями. Якщо від нього відрізати квадрат, то знову залишиться золотий прямокутник. Цей процес можна продовжувати до безкінечності. А якщо провести діагональ першого і другого прямокутника, то точка їх перетину належатиме всім золотим прямокутникам, які одержали. Є і золотий трикутник (рівнобедрений трикутник, у якого відношення довжини бічної сторони до довжини основи дорівнює 1,618), і золотий кубоїд (прямокутний паралелепіпед з ребрами, що мають довжини 1,618, 1 і 0,618). Золотий перетин не є штучним явищем. Воно дуже широко поширене в природі: золотий перетин можна знайти в пропорціях тіл багатьох рослин і тварин, а також морських раковин і пташиних яєць.
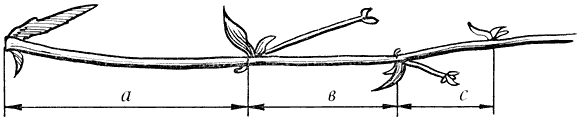
Приклад використання золотого перетину в рослинному світі: цикорій.
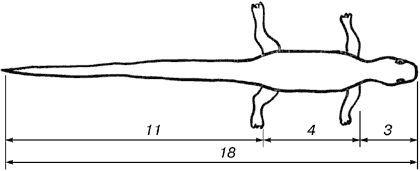
Приклад використання золотого перетину в тваринному світі: ящірка живородюча.
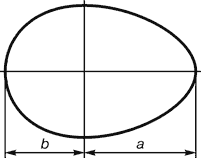
Приклад використання золотого перетину в тваринному світі: пташине яйце.
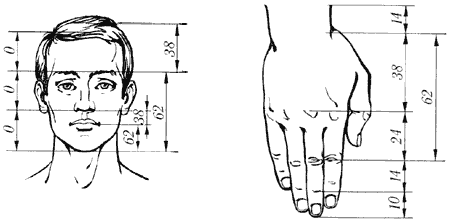
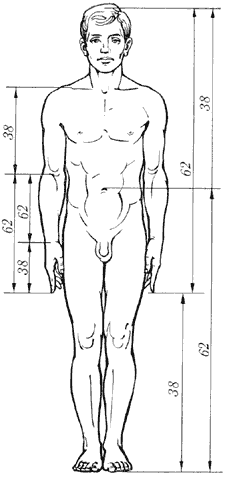
Але найбільш вражаючий приклад "застосування" природою принципу золотого перетину — людське тіло. Воно цілком і його частини (обличчя, руки, грона рук і т. д.) наскрізь пронизані пропорцією 1,618.
Золоті пропорції в частинах тіла людини.
Золоті пропорції в фігурі людини.
Принцип золотого перетину був відкритий людьми ще у глибокій старовині. Знамениті єгипетські піраміди в Гізі, наприклад, засновані на пропорціях золотого перетину. Молодші мексиканські піраміди і античний храм Парфенон також містять в собі пропорцію 1,618.
З золотим перетином пов'язано ім'я італійського математика Фібоначчі. Ряд чисел 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 і т.д. відомий як ряд Фібоначчі. Отримав він цей ряд, розмірковуючи на тему про те, скільки пар кроликів народиться від однієї пари (при місячній розгляді). Кожен член ряду, починаючи з третього, дорівнює сумі двох попередніх, а відношення суміжних чисел ряду наближається до відношенню золотого перетину (21 : 34 = 0,617; 34 : 55 = 0,618). Не зв'язуючи цей ряд із золотим перетином, Фібоначчі відкрив закономірність, до якої незмінно приходили всі дослідники золотого перетину в природі, мистецтві.
З розвитком дизайну і технічної естетики дія закону золотого перетину розповсюдилася на конструювання машин, меблів і т.д. Проектування комп'ютерних інтерфейсів — не виключення. Форми діалогових вікон і елементів управління, сторони яких відносяться як 1,618, дуже привабливі для користувачів. Наприклад, дуже багато захоплень у користувачів програми Chameleon Clock (http://www.softshape.com) викликає така, здавалося б, буденна річ, як вид діалогового вікна Властивості. А все тому, що при його проектуванні використовувався саме принцип золотого перетину.
Продемонструємо на невеличкому прикладі, як же застосовується золотий перетин в розробці інтерфейсів.
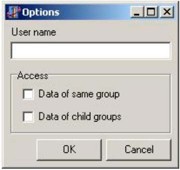
Припустимо, що ми працюємо в Delphi, і нам потрібно привести до пропорцій золотого перетину діалогове вікно (і його елементи), в якому задаються параметри роботи для розробників програми. У вікні розташовані такі елементи: мітка (TLabel) та рядок введення (TEdit), групбокс (TGroupBox) з двома чекбоксами (TCheckBox) та дві кнопки (TButton) "OK", "Cancel". Після початкового компонування вікна отримуємо варіант 1 (рис.1).
Оскільки значення має тільки вміст вікна, а розміри заголовка вікна можуть змінюватися у відповідності з настройками Windows, використовуємо розміри клієнтської частини вікна. Вони становлять 196х166 (ширина і висота). Розміри елементів управління - практично задаються по замовчуванню середовищем розробки. Їх розташування та коригування розмірів зараз нас не цікавлять. Наведемо до пропорції золотого перетину розміри клієнтської частини вікна виходячи зі співвідношення (висота / ширина) = 0,618. Для цього потрібно або зменшити його висоту або збільшити ширину. Оскільки зменшувати висоту нікуди, то збільшимо ширину, яка повинна дорівнювати (висота / 0,382) * 0,618 = 268.
А тепер, клієнтська частина вікна стала форматом 268х166. Тепер можна побудувати ряди Фібоначчі для двох напрямків - горизонталі і вертикалі, в порядку убування від (ширини / висоти) (зростання нам не потрібно). Кожний наступний елемент дорівнює попередньому, помноженому на 0,618. Для горизонталі - 268, 166, 103, 64, 40, 25, 15, 9, 6, 3, для вертикалі - 166, 102, 63, 39, 24, 14, 6, 3. Видно, що вони практично однакові (з урахуванням округлення). Виходячи з цих рядів і будемо корегувати розміри і положення елементів керування у вікні.
Відразу можна помітити, що рядок введення та групбокс мають Left = 6, а мітка Top = 6, що відповідає одному з чисел ряду. Для Label цей параметр дорівнює 7, тому зрушимо позначку вліво на один піксель. Для Edit: Top = 24, що також відповідає одному з чисел ряду. Оскільки ми збільшили ширину вікна, то збільшимо і ширину Edit так, щоб відстань його правої частини становило 6 пікселів від правого краю вікна, точніше, від внутрішньої сторони його рамки (ширина буде 256). Аналогічно збільшимо по ширині і групбокс.
Змістивши кнопки до правого краю вікна (6 пікселів до рамки для кнопки "Cancel"), збільшивши відстань по горизонталі між ними з 5 до 6 пікселів. Відстань до нижньої межі вікна для кнопок (5 пікселів) також збільшимо на одиницю (до 6).
Піднімемо групбокс на 3 пікселі, щоб забезпечити відстань від його нижньої межі до кнопок у 6 пікселів. Чекбокси мають значення Left = 14, а відстань між ними - 9 пікселів, тому їх не міняємо (див. ряд).
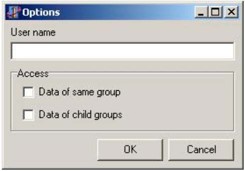
У результаті всіх маніпуляцій отримуємо варіант 2 (рис. 2).
Порівнюючи початковий і підсумковий варіант, можна помітити, що вікно, що зображене на рис. 2, виглядає набагато краще, хоча, на перший погляд, і сталося невиправдане збільшення розмірів деяких його елементів.
При проектуванні вікон програми існує певний мінімальний розмір, який потрібно витримувати між елементами (наприклад, для розглянутого випадку - 6 пікселів). Щоб полегшити роботу, можна використовувати налаштування Delphi "Grid size X", "Grid size X" при включеному чекбоксі "Snap to grid" у вікні "Environement options", вкладка "Preferences". Це не дозволить зробити відстані між елементами менше заданих мінімумів.
Потрібно відзначити, що приведення зовнішнього вигляду інтерфейсу до співвідношенням золотого перетину не повинно бути обов’язковим. Зловживати ним не варто, в усьому потрібна міра. Це бажана, але не завжди необхідна операція. Адже, крім золотого перетину, є й інші правила. Так що золоті пропорції вікон не повинні перекривати "золоті пропорції" логіки, послідовності і т.д. Головне - пізнання, і тоді правила не зроблять розробника своїм полоненим.
Аналогічним чином до пропорцій золотого перетину можна навести і зовнішній вигляд сторінок сайтів, принцип той же самий.