Відмінності між версіями «* Машина Тюринга»
Melani (обговорення • внесок) |
|||
| (не показані 6 проміжних версій 2 учасників) | |||
| Рядок 1: | Рядок 1: | ||
| − | [[Зображення: | + | [[Зображення:turingbombebletchleypark.jpg|center|]] |
| + | |||
| + | '''Машина Тюринга''' — математичне поняття, введене для формального уточнення інтуїтивного поняття алгоритму. Названа на честь англійського математика [[Алана Тюринга]], який запропонував це поняття у 1936. Аналогічну конструкцію машини згодом і незалежно від Тюринга ввів американський математик [http://uk.wikipedia.org/wiki/%D0%95%D0%BC%D1%96%D0%BB%D1%8C_%D0%9F%D0%BE%D1%81%D1%82 Еміль Пост]. | ||
| + | |||
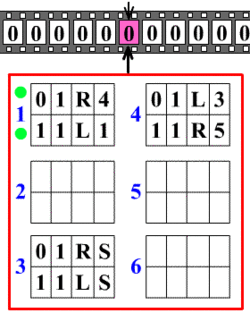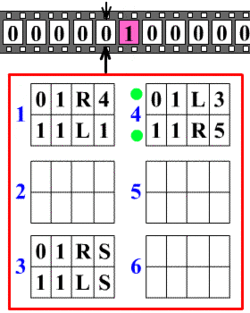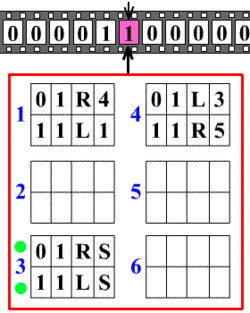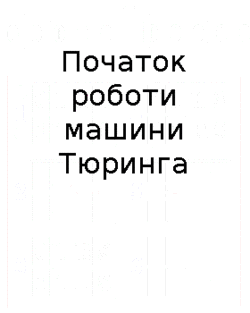
Основна ідея, що лежить в основі машини Тюринга, дуже проста. Машина Тюринга — це абстрактна машина (автомат), що працює зі стрічкою, що складається із окремих комірок, в яких записано символи. Машина також має голівку для запису та читання символів із комірок і яка може рухатись вздовж стрічки. На кожному кроці машина зчитує символ із комірки, на яку вказує голівка та, на основі зчитаного символу та внутрішнього стану, робиться наступний крок. При цьому, машина може змінити свій стан, записати інший символ в комірку або пересунути голівку на одну комірку ліворуч або праворуч. | Основна ідея, що лежить в основі машини Тюринга, дуже проста. Машина Тюринга — це абстрактна машина (автомат), що працює зі стрічкою, що складається із окремих комірок, в яких записано символи. Машина також має голівку для запису та читання символів із комірок і яка може рухатись вздовж стрічки. На кожному кроці машина зчитує символ із комірки, на яку вказує голівка та, на основі зчитаного символу та внутрішнього стану, робиться наступний крок. При цьому, машина може змінити свій стан, записати інший символ в комірку або пересунути голівку на одну комірку ліворуч або праворуч. | ||
Формальні визначення алгоритму з'явилися в тридцятих-сорокових роках 20 століття. Одним із перших було визначення англійського математика Алана Тюринга, який у 1936 році описав схему деякої гіпотетичної (абстрактної) машини і запропонував називати алгоритмами те, що вміє робити така машина. При цьому визначенні, якщо щось не може бути зроблено машиною Тюринга, це вже не алгоритм. Інакше кажучи, Тюринг формалізував правила виконання дій за допомогою опису роботи деякої конструкції. | Формальні визначення алгоритму з'явилися в тридцятих-сорокових роках 20 століття. Одним із перших було визначення англійського математика Алана Тюринга, який у 1936 році описав схему деякої гіпотетичної (абстрактної) машини і запропонував називати алгоритмами те, що вміє робити така машина. При цьому визначенні, якщо щось не може бути зроблено машиною Тюринга, це вже не алгоритм. Інакше кажучи, Тюринг формалізував правила виконання дій за допомогою опису роботи деякої конструкції. | ||
| + | |||
| + | [[Зображення:250px-TuringBeispielDiskretAnimatedGIF uk.gif]] | ||
| + | |||
| + | ''Схематична ілюстрація роботи машини Тюринга.'' | ||
| + | |||
| + | <center>'''Можливості машини Тюринга'''</center> | ||
| + | |||
| + | Багатство можливостей конструкції Тюринга виявляється в тому, що якщо якісь алгоритми A та B реалізуються машинами Тюринга, то можна будувати програми машин Тюринга, які реалізують композиції алгоритмів A та B, наприклад, виконати A, потім виконати B або виконати A. Якщо в результаті утворилося слово так, то виконати B. У протилежному випадку не виконувати B або виконувати по черзі A, B, поки B не дасть відповідь ні. | ||
| + | |||
| + | У інтуїтивному сенсі такі композиції є алгоритмами. Тому їхня реалізація за допомогою машини Тюринга служить одним із засобів обґрунтування універсальності конструкції Тюринга. | ||
| + | |||
| + | Реалізованість таких композицій доводиться у загальному вигляді, незалежно від особливостей конкретних алгоритмів A та B. Доведення полягає в тому, що вказується засіб побудови з програм A та B програми потрібної композиції. Нехай, наприклад, потрібно побудувати машину А*В, еквівалентну послідовному виконанню алгоритмів A та B. Поки виконується алгоритм A, у програмі А*В працює частина A без урахування частини B. Коли алгоритм A дійде до кінця, то замість зупинки відбудеться перехід у перший стан частини B, і потім частина B буде працювати звичайним чином, наче частини A і не було. | ||
| + | |||
| + | Аналогічно конструюють й інші композиції машин Тюринга; щораз будуються загальні правила: що на що змінювати у вихідних програмах. | ||
| + | |||
| + | Описуючи різноманітні алгоритми для машин Тюринга і стверджуючи реалізованість усіляких композицій алгоритмів, Тюринг переконливо показав розмаїтість можливостей запропонованої ним конструкції, що дозволило йому виступити з такою тезою: | ||
| + | |||
| + | <center>''Всякий алгоритм може бути реалізований відповідною машиною Тюринга.''</center> | ||
| + | |||
| + | Це основна гіпотеза теорії алгоритмів у формі Тюринга. Одночасно ця теза є формальним визначенням алгоритму. Завдяки їй можна доводити існування або неіснування алгоритмів, створюючи відповідні машини Тюринга або доводячи неможливість їхньої побудови. Завдяки цьому з'являється загальний підхід до пошуку алгоритмічних рішень. | ||
| + | |||
| + | Якщо пошук рішення наштовхується на перешкоду, то можна використовувати цю перешкоду для доведення неможливості рішення, спираючись на основну гіпотезу теорії алгоритмів. Якщо ж при доказі неможливості виникає своя перешкода, то вона може допомогти просунутися в пошуку рішення, хоча б частково усунувши стару перешкоду. Так, по черзі намагаючись довести то існування, то відсутність рішення, можна поступово наблизитися до розуміння суті поставленої задачі. | ||
| + | |||
| + | Довести тезу Тюринга не можна, тому що в його формулюванні не визначене поняття всякий алгоритм, тобто, ліва частина тотожності. Його можна тільки обґрунтувати, представляючи різноманітні відомі алгоритми у вигляді машин Тюринга. Додаткове обґрунтування цієї тези складається в тому, що пізніше було запропоновано ще декілька загальних визначень поняття алгоритму і щораз вдавалося довести, що, хоча нові алгоритмічні схеми і виглядають інакше, вони в дійсності еквівалентні машинам Тюринга: | ||
| + | |||
| + | <center>''усе, що реалізовано в одній з цих конструкцій, можна зробити і в інших.''</center> | ||
| + | |||
| + | Ці твердження доводяться строго, тому що в них мова йде вже про тотожність формальних схем. | ||
| + | |||
| + | [http://uk.wikipedia.org/wiki/%D0%9C%D0%B0%D1%88%D0%B8%D0%BD%D0%B0_%D0%A2%D1%8E%D1%80%D0%B8%D0%BD%D0%B3%D0%B0 Більш детальніше про роботу машини Тюринга читай тут] | ||
| + | |||
| + | [http://video.online.ua/342425/mashina-tyuringa-iz-lego/ Відео: Машина Тюринга] | ||
Поточна версія на 17:39, 29 жовтня 2012
Машина Тюринга — математичне поняття, введене для формального уточнення інтуїтивного поняття алгоритму. Названа на честь англійського математика Алана Тюринга, який запропонував це поняття у 1936. Аналогічну конструкцію машини згодом і незалежно від Тюринга ввів американський математик Еміль Пост.
Основна ідея, що лежить в основі машини Тюринга, дуже проста. Машина Тюринга — це абстрактна машина (автомат), що працює зі стрічкою, що складається із окремих комірок, в яких записано символи. Машина також має голівку для запису та читання символів із комірок і яка може рухатись вздовж стрічки. На кожному кроці машина зчитує символ із комірки, на яку вказує голівка та, на основі зчитаного символу та внутрішнього стану, робиться наступний крок. При цьому, машина може змінити свій стан, записати інший символ в комірку або пересунути голівку на одну комірку ліворуч або праворуч.
Формальні визначення алгоритму з'явилися в тридцятих-сорокових роках 20 століття. Одним із перших було визначення англійського математика Алана Тюринга, який у 1936 році описав схему деякої гіпотетичної (абстрактної) машини і запропонував називати алгоритмами те, що вміє робити така машина. При цьому визначенні, якщо щось не може бути зроблено машиною Тюринга, це вже не алгоритм. Інакше кажучи, Тюринг формалізував правила виконання дій за допомогою опису роботи деякої конструкції.
Схематична ілюстрація роботи машини Тюринга.
Багатство можливостей конструкції Тюринга виявляється в тому, що якщо якісь алгоритми A та B реалізуються машинами Тюринга, то можна будувати програми машин Тюринга, які реалізують композиції алгоритмів A та B, наприклад, виконати A, потім виконати B або виконати A. Якщо в результаті утворилося слово так, то виконати B. У протилежному випадку не виконувати B або виконувати по черзі A, B, поки B не дасть відповідь ні.
У інтуїтивному сенсі такі композиції є алгоритмами. Тому їхня реалізація за допомогою машини Тюринга служить одним із засобів обґрунтування універсальності конструкції Тюринга.
Реалізованість таких композицій доводиться у загальному вигляді, незалежно від особливостей конкретних алгоритмів A та B. Доведення полягає в тому, що вказується засіб побудови з програм A та B програми потрібної композиції. Нехай, наприклад, потрібно побудувати машину А*В, еквівалентну послідовному виконанню алгоритмів A та B. Поки виконується алгоритм A, у програмі А*В працює частина A без урахування частини B. Коли алгоритм A дійде до кінця, то замість зупинки відбудеться перехід у перший стан частини B, і потім частина B буде працювати звичайним чином, наче частини A і не було.
Аналогічно конструюють й інші композиції машин Тюринга; щораз будуються загальні правила: що на що змінювати у вихідних програмах.
Описуючи різноманітні алгоритми для машин Тюринга і стверджуючи реалізованість усіляких композицій алгоритмів, Тюринг переконливо показав розмаїтість можливостей запропонованої ним конструкції, що дозволило йому виступити з такою тезою:
Це основна гіпотеза теорії алгоритмів у формі Тюринга. Одночасно ця теза є формальним визначенням алгоритму. Завдяки їй можна доводити існування або неіснування алгоритмів, створюючи відповідні машини Тюринга або доводячи неможливість їхньої побудови. Завдяки цьому з'являється загальний підхід до пошуку алгоритмічних рішень.
Якщо пошук рішення наштовхується на перешкоду, то можна використовувати цю перешкоду для доведення неможливості рішення, спираючись на основну гіпотезу теорії алгоритмів. Якщо ж при доказі неможливості виникає своя перешкода, то вона може допомогти просунутися в пошуку рішення, хоча б частково усунувши стару перешкоду. Так, по черзі намагаючись довести то існування, то відсутність рішення, можна поступово наблизитися до розуміння суті поставленої задачі.
Довести тезу Тюринга не можна, тому що в його формулюванні не визначене поняття всякий алгоритм, тобто, ліва частина тотожності. Його можна тільки обґрунтувати, представляючи різноманітні відомі алгоритми у вигляді машин Тюринга. Додаткове обґрунтування цієї тези складається в тому, що пізніше було запропоновано ще декілька загальних визначень поняття алгоритму і щораз вдавалося довести, що, хоча нові алгоритмічні схеми і виглядають інакше, вони в дійсності еквівалентні машинам Тюринга:
Ці твердження доводяться строго, тому що в них мова йде вже про тотожність формальних схем.