Відмінності між версіями «Мережі Петрі»

Матеріал з Вікі ЦДУ
Перейти до: навігація, пошук
(→‎Мережа Петрі)
 
(не показані 17 проміжних версій 2 учасників)
Рядок 1: Рядок 1:
 
== Мережа Петрі==
 
== Мережа Петрі==
−
[[Image:Проста мережа Петрі.JPG|thumb|right|Рис.1 Проста мережа Петрі з одним переходом, трьома вузлами, два з яких містять маркери]]
+
 
  
 
'''Мережа Петрі – це графічний і математичний засіб моделювання систем і процесів.'''  
 
'''Мережа Петрі – це графічний і математичний засіб моделювання систем і процесів.'''  
Рядок 8: Рядок 8:
 
Як правило, мережами Петрі моделюють паралельні (синхронні та асинхронні) системи і процеси. Спочатку запропоновані в докторській дисертації Карла Петрі в 1962 році вони одержали подальший розвиток у роботах таких вчених як Тадао Мурата, Курт Йенсен, Віталій Котов, Анатолій Слєпцов. В останні часи проводиться щорічна конференція «Застосування і теорія мереж Петрі», видається в Боні інформаційний бюлетень «Новини мереж Петрі» (Petri Net Newsletter), відомо декілька сот моделюючих систем для різних програмно-апаратних платформ, існують реалізації процесорів мереж Петрі. Галузі застосування мереж Петрі включають дослідження телекомунікаційних мереж, мережних протоколів, обчислювальних систем і обчислювальних процесів, виробничих і організаційних систем.
 
Як правило, мережами Петрі моделюють паралельні (синхронні та асинхронні) системи і процеси. Спочатку запропоновані в докторській дисертації Карла Петрі в 1962 році вони одержали подальший розвиток у роботах таких вчених як Тадао Мурата, Курт Йенсен, Віталій Котов, Анатолій Слєпцов. В останні часи проводиться щорічна конференція «Застосування і теорія мереж Петрі», видається в Боні інформаційний бюлетень «Новини мереж Петрі» (Petri Net Newsletter), відомо декілька сот моделюючих систем для різних програмно-апаратних платформ, існують реалізації процесорів мереж Петрі. Галузі застосування мереж Петрі включають дослідження телекомунікаційних мереж, мережних протоколів, обчислювальних систем і обчислювальних процесів, виробничих і організаційних систем.
  
−
==Комп'ютерні моделюючі системи==
+
==Прості мережі Петрі==
 +
[[Image:Проста мережа Петрі.JPG|thumb|right|Рис.1 Проста мережа Петрі з одним переходом, трьома вузлами, два з яких містять маркери]]
  
−
Pndpi, Tina, Design/CPN
+
Мережа Петрі є орієнтованим дводольним графом, який має чотири базових елементи: вузди, або місця(places), переходи(transitions), дуги(arcs) і маркери(tokens).
 +
Вузли позначаються кружками і визначають стан, в якому може знаходитись мережа або її частина.
 +
Переходи-це активні елементи мережі, які позначають дії, виконувані під час спрацювання переходів. Для того щоб перехід міг спрацювати, необхідне виконання певних умов, які визначаються наявністю маркерів у вузлах мережі, з'єднаних з переходом. Якщо умови настання подій виконано, то вважають, що перехід збуджений. Переходи позначаються короткими вертикальними або горизонтальними лініями.
 +
Вузли та переходи з'єднуються орієнтованими ребрами (дугами). Два вузли або два переходи з'єднуватись дугами не можуть.
  
−
== Визначення ==
+
Функціонування мережі Петрі можна описати так: вузли як певні умови, а переходи-як події. Таким чином, стан мережі в кожний момент часу задається системою умов. Для зручності задання  умов мережі Петрі вводяться маркери(фішки), які зображуються крапками всередині вузлів. Виникнення певної комбінації маркерів у вузлах приводить до настання деякої події, яка у свою чергу викликає зміну стану умов мережі. Стан маркування або стан мережі Петрі визначаеться сукупністю маркерів кожного окремого вузда мережі.
−
Мережа Петрі задається у вигляді [[Мічений граф|маркованого]] [[Дводольний граф|дводольного]] [[Орієнтований граф|орієнтованого]] [[Граф (математика)|графу]]. Розрізняють два види вершин:
+
−
* Позиції. '''P''' — множина позицій,
+
−
* Переходи. '''T''' — множина переходів.
+
  
−
[[Ребро графа|Ребра]] називають ''дугами''. [[Петля в графі|Петлі]] в графі мереж Петрі неможливі, оскільки дуги можуть з'єднувати лише вершини різних типів (позиції та переходи). Позиції що з'єднані дугами з переходом називають вхідними та вихідними для цього переходу, відповідно до напрямку цих дуг.
+
[[Image:Спрацювання переходу.JPG|thumb|left|600px|Рис.2 Графічне зображення спрацювання переходу]]
  
−
Кожній позиції приписують деяке ціле додатнє число<br />
+
Перехід, в якого всі вхвдні вузли містять маркери, називається збудженим (Рис.1). Збуджений перехід може спрацювати, після чого всі маркери із вхідних вузлів переходу перемістятся у вихідні(Рис.2). Таким чином, настає подія, яка змінює стан мережі.
−
: <math>\mu_p \in \mathbb{N} \cup \{0\}</math><br />
+
−
що називається маркуванням. Сукупність маркувань всіх позицій можна записувати у вигляді [[Вектор|вектора]].
+
  
−
Таким чином, для того щоб задати мережу Петрі, необхідно задати пару<br />
+
Якщо одночасно збуджуються кілька переходів мережі, виникає невизначеність, тому одночасне спрацювання кількох переходів у мережі Петрі неможливе, тобто переходи спрацьовують послідовно, миттєво. Незважаючи на те, що маркери змінюють своє положення у вузлах, прості мережі Петрі- це статичні моделі, в яких не враховується динаміка в часі (зміна станів мережі не залежить від моментів часу).
−
: <math>\left\langle\mathbf N, \mu_0 \right\rangle</math><br />
+
Для того щоб за допомогою мережі Петрі відтворити динаміку роботи деякої детермінованої динамічної системи в часі, необхідно зазначати моменти спрацьовування переходів. Такі можливості мають тільки розширення мереж Петрі, в яких спрацювання переходів здійснюється в задані моменти модельного часу з деяким постійним кроком дельта(т).
−
де <math>\mu_0 = \left\{\mu(p_1),\mu(p_2),...\mu(p_n)\right\}</math>&nbsp;— вектор маркування позицій, <math>\mathbf N</math>&nbsp;— структура мережі Петрі:<br />
+
−
: <math>\mathbf N = \left\langle\mathbf P, \mathbf T, \mathbf I, \mathbf O \right\rangle</math>.<br />
+
−
де <math>\mathbf P</math>&nbsp;— [[множина|множина]] позицій, <math>\mathbf T</math>&nbsp;— [[множина|множина]] переходів, <math>\mathbf I</math>&nbsp;— вхідна функція, <math>\mathbf O</math>&nbsp;— вихідна функція.<br />
+
−
Вхідна та вихідна функції задаються у вигляді [[множина|множин]] комлектів позицій, які є вхідними та вихідними для заданого переходу:
+
−
: <math>\mathbf I = \left\{\mathbf I(t_j)\right\}</math>, <math>\mathbf \mathbf I(t_j) = \left\{p_k\right\}</math>.<br />
+
−
: <math>\mathbf O = \left\{\mathbf O(t_j)\right\}</math>, <math>\mathbf \mathbf O(t_j) = \left\{p_k\right\}</math>.<br />
+
−
Комплект&nbsp;— узагальнення [[множина|множини]], в якому допускається багаторазове включення однакових елементів. Для комплектів визначається операція кратності. Для запису функції кратності використовується символ #. Кратність вхідної (вихідної) позиції <math>p_i</math> для переходу <math>t_j</math> це кількість появ позиції <math>p_i</math> у вхідному (вихідному) комплекті переходу <math>t_j</math>:
+
−
: <math>\#(p_i, \mathbf I(t_j))</math>.<br />
+
−
Альтернативною формою представлення вхідної та вихідної функції є задання множини дуг та окремого вектору кратності (ваги) дуг.<br />
+
−
Виконання переходу можливе лише за наявності достатньої кількості «фішок» у його вхідних позиціях. Умова можливості виконання переходу <math>t_j</math>:<br />
+
−
: <math>\mu(p_i) \ge \;\#\left(p_i, \mathbf I(t_j)\right) \forall p_i\in\mathbf P</math>.<br />
+
−
Результатом виконання переходу є зміна кількості «фішок» у вхідних та вихідних позиціях цього переходу, тобто зміна маркування (стану) мережі Петрі. Нове маркування <math>\mu^{i+1}</math> визначається таким співвідношенням:<br />
+
−
: <math>\mu^{i+1}(p_i) = \mu^i(p_i) - \#(p_i, \mathbf I(t_j)) + \#(p_i, \mathbf O(t_j))</math>,<br />
+
−
де <math>t_j</math>&nbsp;— перехід що виконується <math>\mu^{i}(p_i)</math>&nbsp;— попереднє маркування.<br />
+
−
Цей вираз дозволяє записати векторну функцію наступного стану, яка виражає наступне маркування мережі Петрі через попереднє маркування та перехід що виконується:
+
−
: <math>\mu^{i+1} = \delta\left(\mu^i, t_j\right)</math>.<br />
+
−
Для заданої послідовності виконання переходів <math>\sigma = \left\langle t_{j1}, t_{j2},... ,t_{jl}\right\rangle</math> використовується розширена функція наступного стану:
+
−
: <math>\mu^{i+l} = \delta\left(\mu^i, \sigma\right) = \delta\left(... \delta\left(\delta\left(\mu^i, t_{j1}\right), t_{j2}\right),... ,t_{jl}\right)</math>.<br />
+
  
−
Виконання переходів є атомарним, тобто перехід змінює стан всіх вхідних та вихідних позицій [[транзакція|однією дією]], яка не може бути перервана виконанням іншого переходу.
+
== Моделювання систем за допомогою мереж Петрі ==
−
Виконання мереж Петрі в цілому є недетермінованим:
+
−
:# відразу декілька переходів можуть бути дозволеними, і кожен з них може бути виконаний
+
−
:# дозволені переходи не обов'язково виконуються. Дозволений перехід '''може''' бути виконаний.
+
−
Взагалі, мережі Петрі не розглядають поняття «часу» виконання переходу, а лише послідовність виконань. За допомогою мереж Петрі можна моделювати такі якості як:
+
−
* [[Асинхронність|асинхронність]],
+
−
* [[Конфліктність|конфліктнісь]],
+
−
* [[Паралелізм (інформатика)|паралелізм]].
+
  
 +
Прості мережі Петрі містять лише три основних елементи% вузли, переходи та маркери. Тому побудувати за їх допомогою моделей складних динамічних систем, в яких протікає велика кількість взаємодіючих паралельних і асинхронних процесів та існує багато інформаційних і матеріальних потоків, стає досить складною та громіздкою процедурою. Це помітно звужує Клас моделей систем,  які можна побудувати на основі простих мереж Петрі які дають можливість значно спростити побудову складних моделей і їх графічне зображення.
 +
 +
=== Розширення простих мереж Петрі ===
 +
 +
Розширення мережі Петрі - це така їх модифікація, яка збільшує можливості мережі стосовно опису та моделювання систем. Існують різні розширення мереж Петрі, орієнтовані на моделювання систем різних типів: стохастичних, динамічних, предикатних та ін. Кольорові мережі Петрі дають змогу значно зменшити розміри мереж, які використовуються, наприклад, для опися моделей складних паралельних обчислювальних систем.
 +
На практиці широко використовуються проблемно-орієнтовані розширення мереж Петрі, серед яких найбільш відомі Е-мережі, комбі-мережі, FIFI-мережі, М-мережі та ін.
 +
У простих мережах Петрі допускається наявність у вузлі лише одного маркера, тоді як урозширених мережах кожний вузол може містити кілька маркерів у вузлі позначає число поряд з вузлом. Відповідно для цих вузлів змінюються і правила маркування:
 +
 +
[[Image:Графічне позначення дуги заперечення.JPG|thumb|right|600px|Рис.3 Графічне позначення дуги заперечення]]
 +
* перехід збуджується тільки тоді, коли число, яке визначає кількість маркерів у кожному вхідному вузлі, більше або дорівнює одиниці;
 +
* Якщо збуджений перехід спрацьовує, то число маркерів у всіх вхідних вузлах, які містять маркери, зменшуються на одиницю, а в усіх вихідних вузлах - збільшується на одиницю. Певна річ, кількість маркерів не може біти від'ємним значенням.
 +
 +
Мережі Петрі достатньо для опису причинно-наслідкових подій, які виникають у системах, однак мережі не забезпечують повну спільність з логічними операціями. Зрозуміло, що проста мережа Петрі відтворює роботу тільки логічного елемента "І" ("AND"), тому за допомогою цієї мережі не можна змоделювати збудження переходу, коли вхідний вузол не має маркерів(логічний оператор заперечення "НІ").
 +
Для цього в розширених мережах усводяться дуги заперечення, які зображуються у вигляді лінії з кружечком на кінці замість стрілки (Рис.3) і не мають дугової ваги (дугова вага визначає пропускну здатність дуги). Дуги, визначені раніше, розглядаються як позитивні. Вони  завжди направлені від деякого вузла до переходу і не можуть мати зворотнього напрямку. Наявність дуги заперечення змінює правила маркування на такі:
 +
 +
* перехід збуджується лише тоді, коли число, яке визначає кількість маркерів кожного вхідного вузла з позитивною дугою, більше або
 +
[[Image:Введення ваги дуги.jpg|thumb|left|600px|Рис.4 Введення ваги дуги]]
 +
дорівнює одиниці, та коли кількість маркерів кожного вхідного вузла з дугою заперечення дорівнює нулю;
 +
 +
* якщо збуджений перехід спрацьовує, то число маркерів усіх вхідних вузлів з позитивною дугою зменшується на одиницю, у той час як кількість маркерів вхідних вузлів з дугами заперечення залишається незмінною. Кількість маркерів усіх вихідних вузлів збільшується на одиницю.
 +
 +
Для кожної позитивної дуги можна задати певний ваговий коефіцієнт (або вагу), рівний одиниці або більший за неї(Рис.4). За замовчуванням ваговий коефіцієнт дуги дорівнює одиниці. Тоді збудження та спрацьовування переходу відбувається за такими правилами:
 +
 +
* прехід збуджується тільки тоді, коли кількість маркерів у кожному вхідному вузлі більше ваги дуги або дорівнює їй, а для дуги заперечення дорівнює нулю;
 +
 +
* у разі перемикання переходу кількість маркерів кожного вхідного вузла зменшується на відповідну вагу вхідної дуги та залишається незмінною для дуг заперечень. Кількість маркерів кожного вихідного вузла збільшується на вагу відповідної вихідної дуги.
 +
 +
 +
=== Формалізоване зображення моделі за допомогою мережі Петрі ===
 +
 +
Один із найсладніших етапів створення моделі- це вибір методу її формалізації. Зазвичай існує кілька підходів до зображення моделі системи і мережі Петрі. Продемонструємо на прикладах, як перейти від змістовної постановки задачі до формальної моделі.
 +
 +
=== Розширення можливостей вузлів під час моделювання ===
 +
 +
Подальше розширення можливостей мереж Петрі для виконання завдань моделювання пов'язане з переходом від використання вузлів з маркерами і переходів до використання сховищ даних (вузол з деякою структурою даних) і потоків даних.
 +
Вище зазначалось, що в мережі Петрі всі допустимі стани моделі позначаються вузлами з маркерами. У загальному випадку вузли виступають як сховища даних заданого об'єму, а переходи - як потоки даних. Можливості вузлів мережі Петрі можна значно розширити, якщо маркерам призначати різні типи даних, наприклад рядки символів, цілі або дійсні числа, множини, структури, як це робиться в мовах програмування. Тоді у разі зображення вузлів з такими маркерами необхідно вказувати типи даних і визначати максимальну кількість маркерів кожного типу, які можуть знаходитись у вузлі.
 +
Існує ще одна можливість розширення функцій вузлів - зазначити режим доступу до маркерів, тобто задати, яким чином маркери(дані) надходять до вузлів та як вони в них вилучаються. Це дає змогу формувати у вузлах черги маркерів подібно тому, чк створюються черги вимог у СМО. У Табл.1 наведено основні режими доступу до вузлів.
 +
 +
''' Табл.1 Основні режими доступу до вузлів у рожширеннях мереж Петрі. '''
 +
{| border=2
 +
 +
|-
 +
! Режим доступу
 +
! Опис
 +
 +
|-
 +
| RAM
 +
| Принцип випадкового доступу. Маркер, який надійшов до вузла, розміщується в черзі випадково. У разі спрацювання переходу маркер, який вилучается з черги, вибирається випадково.
 +
 +
|-
 +
| FIFO
 +
| Принцип "перший прийшов-перший пішов". Маркер, який надійшов до вузла, розміщується в черзі останнім. У разі спрацювання переходу вилучаеться перший маркер черги.
 +
 +
|-
 +
| LIFO
 +
| Принцип "останній прийшов-перший пішов". Маркер, який надійшов до вузла останнім, розміщується в черзі першим. У разі спрацювання переходу вилучається перший маркер.
 +
 +
|-
 +
| FIFORAM
 +
| Принцип "прийшов випадково - перший покинув". Маркер, який надійшов, розміщується в черзі випадково. У разі спрацювання переходу з черги вилучається перший маркер.
 +
|-
 +
| LIFORAM
 +
| Принцип "прийшов випадково - останній покинув". Маркер, який надійшов, розміщується в черзі випадково. У разі спрацювання переходу з черги вилучаеться перший маркер.
 +
 +
|}
 +
 +
Вибір режимів формування черги і вилучення із неї маркерів залежить від того, в якій послідовності потрібно перевіряти маркери у вузлах. Тому навряд чи можна дати загальну пораду відносно того, які режими доступу використовувати. У простих мережах Петрі автоматичного використовується режим довільного доступу (порядок поставлення маркерів у чергу та порядок їх вилучення для них не має значення).
 +
Розширення можливостей вузлів мереж Петрі є досить зручним засобом для моделювання матеріальних та інформаційних потоків у виробничих системах.
  
 
== Дослідження мережі Петрі ==
 
== Дослідження мережі Петрі ==
Рядок 71: Рядок 113:
 
# Покриття&nbsp;— досліджує існування послідовності виконань переходів при якій можна досягнути маркування що покриває, тобто є більшим за задане маркування.
 
# Покриття&nbsp;— досліджує існування послідовності виконань переходів при якій можна досягнути маркування що покриває, тобто є більшим за задане маркування.
  
−
Умова зберігальності може бути послаблена, для чого вводять поняття функції ваги:<br />
+
Умова зберігальності може бути послаблена, для чого вводять поняття функції ваги, яка залишається постійною під час роботи.<br />
 
: <math>
 
: <math>
 
\mathbf W:\qquad(\mathbf T \times \mathbf P) \cup (\mathbf P \times \mathbf T) \to \mathbb N \cup \{0\}</math><br />
 
\mathbf W:\qquad(\mathbf T \times \mathbf P) \cup (\mathbf P \times \mathbf T) \to \mathbb N \cup \{0\}</math><br />
−
яка залишається постійною під час роботи.
 
  
−
Більшість досліджень мереж Петрі можна звести до побудови дерева досяжності.
+
==Види мереж Петрі==
 +
Деякі види мереж Петрі:
  
 +
* Тимчасова мережа Петрі - переходи мають вагою, визначаючу тривалість спрацьовування (затримку).
  
−
==Список використаної літератури==
+
* Стохастична мережа Петрі - затримки є випадковими величинами.
  
−
1.  
+
* Функціональна мережа Петрі - затримки визначаються як функції деяких аргументів, наприклад, кількості міток в будь-яких позиціях, стану деяких переходів.
  
−
2. Зайцев Д.А. Мережі Петрі і моделювання систем: Навчальній посібник // , Одеса 2006
+
* Кольорова мережа Петрі - мітки можуть бути різних типів, які позначені різними кольорами, тип мітки може бути використаний як аргумент у функціональних мережах.
  
−
3. Зайцев Д.А. Математичні моделі дискретних систем: Навчальний посібник // Одеса: ОНАЗ ім. О.С. Попова, 2004. – 40 с.
+
* Інгібіторна мережа Петрі - можливі інгібіторні дуги, що забороняють спрацьовування переходу, якщо у вхідній позиції знаходиться мітка.
  
−
4. Математичні основи теорії телекомунікаційних  систем / Підручник за загальною редакцію В.В. Поповського. – Харків, ТОВ «Компанія СМІТ», 2006. – 564 с.
+
* Ієрархічна мережа - містить не миттєві переходи, в які вкладено інші, можливо, також ієрархічні мережі. Спрацювання такого переходу характеризує виконання повного життєвого циклу вкладеної мережі.
  
−
5. Питерсон Дж. Теория сетей Петри и моделирование систем. – М. Мир, 1984. – 264 с.
+
* WF-мережі
  
−
6. Котов В.Е. Сети Петри. – М.: Наука, 1984. – 160 с.
+
==Проблеми розв’язності мереж Петрі==
  
−
7. Ачасова С.М., Бандман О.Л. Корректность параллельных вычислительных процессов. – Н.: Наука, 1990. – 253 с.  
+
На даний час існують такі проблеми розв’язності для мереж Петрі:
 +
 
 +
1. Проблема досяжності (тупикової) розмітки.
 +
 
 +
2. Проблема досяжності переходу.
 +
 
 +
3. Проблема життєвості.
 +
 
 +
4. Проблема еквівалентність.
 +
 
 +
5. Проблема рівності.
 +
 
 +
6. Проблема k-обмеженості.
 +
 
 +
7. Проблема обмеженості.
 +
 
 +
 
 +
==Комп'ютерні моделюючі системи==
 +
 
 +
1. Pndpi
 +
 +
2. Tina
 +
 
 +
3. Design/CPN
 +
 
 +
4. [[HPSim|HPSim]]
 +
 
 +
==Список використаної літератури==
  
−
8. Слепцов А.И., Юрасов А.А. Автоматизация проектирования управляющих систем гибких автоматизированных производств / Под ред. Б.Н.Малиновского. – К.: Технiка, 1986. – 160 с.
+
# Зайцев Д.А. Мережі Петрі і моделювання систем: Навчальній посібник // , Одеса 2006
 +
# Зайцев Д.А. Математичні моделі дискретних систем: Навчальний посібник // Одеса: ОНАЗ ім. О.С. Попова, 2004. – 40 с.
 +
# Математичні основи теорії телекомунікаційних  систем / Підручник за загальною редакцію В.В. Поповського. – Харків, ТОВ «Компанія СМІТ», 2006. – 564 с.
 +
# Питерсон Дж. Теория сетей Петри и моделирование систем. – М. Мир, 1984. – 264 с.
 +
# Котов В.Е. Сети Петри. – М.: Наука, 1984. – 160 с.
 +
# Ачасова С.М., Бандман О.Л. Корректность параллельных вычислительных процессов. – Н.: Наука, 1990. – 253 с.
 +
# Слепцов А.И., Юрасов А.А. Автоматизация проектирования управляющих систем гибких автоматизированных производств / Под ред. Б.Н.Малиновского. – К.: Технiка, 1986. – 160 с.

Поточна версія на 06:52, 27 травня 2013

Мережа Петрі

Мережа Петрі – це графічний і математичний засіб моделювання систем і процесів.

Графічно представляється у вигляді дводольного орієнтованого мультиграфу з маркерами («фішками») (маркований орієнтований граф), який має дві групи вершин: позиції та переходи. Позиції можуть бути пустими або маркованими та визначають <стан> мережі. Переходи визначають дії. Орієнтовані ребра графу задають зв'язки між позиціями та переходами. Процес функціонування мережі Петрі полягає в послідовному «виконанні» переходів, та відповідному перерахункові кількості «фішок» у позиціях. Дуги можуть бути кратними, коли два вузли з'єднані більше ніж однією дугою однакового напрямку. Альтернативно, для відображення кратності дуг може використовуватися функція «ваги» дуг.

Як правило, мережами Петрі моделюють паралельні (синхронні та асинхронні) системи і процеси. Спочатку запропоновані в докторській дисертації Карла Петрі в 1962 році вони одержали подальший розвиток у роботах таких вчених як Тадао Мурата, Курт Йенсен, Віталій Котов, Анатолій Слєпцов. В останні часи проводиться щорічна конференція «Застосування і теорія мереж Петрі», видається в Боні інформаційний бюлетень «Новини мереж Петрі» (Petri Net Newsletter), відомо декілька сот моделюючих систем для різних програмно-апаратних платформ, існують реалізації процесорів мереж Петрі. Галузі застосування мереж Петрі включають дослідження телекомунікаційних мереж, мережних протоколів, обчислювальних систем і обчислювальних процесів, виробничих і організаційних систем.

Прості мережі Петрі

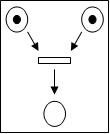
Рис.1 Проста мережа Петрі з одним переходом, трьома вузлами, два з яких містять маркери

Мережа Петрі є орієнтованим дводольним графом, який має чотири базових елементи: вузди, або місця(places), переходи(transitions), дуги(arcs) і маркери(tokens). Вузли позначаються кружками і визначають стан, в якому може знаходитись мережа або її частина. Переходи-це активні елементи мережі, які позначають дії, виконувані під час спрацювання переходів. Для того щоб перехід міг спрацювати, необхідне виконання певних умов, які визначаються наявністю маркерів у вузлах мережі, з'єднаних з переходом. Якщо умови настання подій виконано, то вважають, що перехід збуджений. Переходи позначаються короткими вертикальними або горизонтальними лініями. Вузли та переходи з'єднуються орієнтованими ребрами (дугами). Два вузли або два переходи з'єднуватись дугами не можуть.

Функціонування мережі Петрі можна описати так: вузли як певні умови, а переходи-як події. Таким чином, стан мережі в кожний момент часу задається системою умов. Для зручності задання умов мережі Петрі вводяться маркери(фішки), які зображуються крапками всередині вузлів. Виникнення певної комбінації маркерів у вузлах приводить до настання деякої події, яка у свою чергу викликає зміну стану умов мережі. Стан маркування або стан мережі Петрі визначаеться сукупністю маркерів кожного окремого вузда мережі.

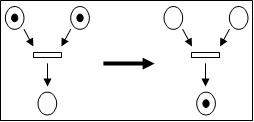
Рис.2 Графічне зображення спрацювання переходу

Перехід, в якого всі вхвдні вузли містять маркери, називається збудженим (Рис.1). Збуджений перехід може спрацювати, після чого всі маркери із вхідних вузлів переходу перемістятся у вихідні(Рис.2). Таким чином, настає подія, яка змінює стан мережі.

Якщо одночасно збуджуються кілька переходів мережі, виникає невизначеність, тому одночасне спрацювання кількох переходів у мережі Петрі неможливе, тобто переходи спрацьовують послідовно, миттєво. Незважаючи на те, що маркери змінюють своє положення у вузлах, прості мережі Петрі- це статичні моделі, в яких не враховується динаміка в часі (зміна станів мережі не залежить від моментів часу). Для того щоб за допомогою мережі Петрі відтворити динаміку роботи деякої детермінованої динамічної системи в часі, необхідно зазначати моменти спрацьовування переходів. Такі можливості мають тільки розширення мереж Петрі, в яких спрацювання переходів здійснюється в задані моменти модельного часу з деяким постійним кроком дельта(т).

Моделювання систем за допомогою мереж Петрі

Прості мережі Петрі містять лише три основних елементи% вузли, переходи та маркери. Тому побудувати за їх допомогою моделей складних динамічних систем, в яких протікає велика кількість взаємодіючих паралельних і асинхронних процесів та існує багато інформаційних і матеріальних потоків, стає досить складною та громіздкою процедурою. Це помітно звужує Клас моделей систем, які можна побудувати на основі простих мереж Петрі які дають можливість значно спростити побудову складних моделей і їх графічне зображення.

Розширення простих мереж Петрі

Розширення мережі Петрі - це така їх модифікація, яка збільшує можливості мережі стосовно опису та моделювання систем. Існують різні розширення мереж Петрі, орієнтовані на моделювання систем різних типів: стохастичних, динамічних, предикатних та ін. Кольорові мережі Петрі дають змогу значно зменшити розміри мереж, які використовуються, наприклад, для опися моделей складних паралельних обчислювальних систем. На практиці широко використовуються проблемно-орієнтовані розширення мереж Петрі, серед яких найбільш відомі Е-мережі, комбі-мережі, FIFI-мережі, М-мережі та ін. У простих мережах Петрі допускається наявність у вузлі лише одного маркера, тоді як урозширених мережах кожний вузол може містити кілька маркерів у вузлі позначає число поряд з вузлом. Відповідно для цих вузлів змінюються і правила маркування:

Рис.3 Графічне позначення дуги заперечення
  • перехід збуджується тільки тоді, коли число, яке визначає кількість маркерів у кожному вхідному вузлі, більше або дорівнює одиниці;
  • Якщо збуджений перехід спрацьовує, то число маркерів у всіх вхідних вузлах, які містять маркери, зменшуються на одиницю, а в усіх вихідних вузлах - збільшується на одиницю. Певна річ, кількість маркерів не може біти від'ємним значенням.

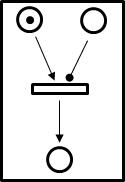
Мережі Петрі достатньо для опису причинно-наслідкових подій, які виникають у системах, однак мережі не забезпечують повну спільність з логічними операціями. Зрозуміло, що проста мережа Петрі відтворює роботу тільки логічного елемента "І" ("AND"), тому за допомогою цієї мережі не можна змоделювати збудження переходу, коли вхідний вузол не має маркерів(логічний оператор заперечення "НІ"). Для цього в розширених мережах усводяться дуги заперечення, які зображуються у вигляді лінії з кружечком на кінці замість стрілки (Рис.3) і не мають дугової ваги (дугова вага визначає пропускну здатність дуги). Дуги, визначені раніше, розглядаються як позитивні. Вони завжди направлені від деякого вузла до переходу і не можуть мати зворотнього напрямку. Наявність дуги заперечення змінює правила маркування на такі:

  • перехід збуджується лише тоді, коли число, яке визначає кількість маркерів кожного вхідного вузла з позитивною дугою, більше або
Рис.4 Введення ваги дуги

дорівнює одиниці, та коли кількість маркерів кожного вхідного вузла з дугою заперечення дорівнює нулю;

  • якщо збуджений перехід спрацьовує, то число маркерів усіх вхідних вузлів з позитивною дугою зменшується на одиницю, у той час як кількість маркерів вхідних вузлів з дугами заперечення залишається незмінною. Кількість маркерів усіх вихідних вузлів збільшується на одиницю.

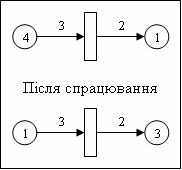
Для кожної позитивної дуги можна задати певний ваговий коефіцієнт (або вагу), рівний одиниці або більший за неї(Рис.4). За замовчуванням ваговий коефіцієнт дуги дорівнює одиниці. Тоді збудження та спрацьовування переходу відбувається за такими правилами:

  • прехід збуджується тільки тоді, коли кількість маркерів у кожному вхідному вузлі більше ваги дуги або дорівнює їй, а для дуги заперечення дорівнює нулю;
  • у разі перемикання переходу кількість маркерів кожного вхідного вузла зменшується на відповідну вагу вхідної дуги та залишається незмінною для дуг заперечень. Кількість маркерів кожного вихідного вузла збільшується на вагу відповідної вихідної дуги.


Формалізоване зображення моделі за допомогою мережі Петрі

Один із найсладніших етапів створення моделі- це вибір методу її формалізації. Зазвичай існує кілька підходів до зображення моделі системи і мережі Петрі. Продемонструємо на прикладах, як перейти від змістовної постановки задачі до формальної моделі.

Розширення можливостей вузлів під час моделювання

Подальше розширення можливостей мереж Петрі для виконання завдань моделювання пов'язане з переходом від використання вузлів з маркерами і переходів до використання сховищ даних (вузол з деякою структурою даних) і потоків даних. Вище зазначалось, що в мережі Петрі всі допустимі стани моделі позначаються вузлами з маркерами. У загальному випадку вузли виступають як сховища даних заданого об'єму, а переходи - як потоки даних. Можливості вузлів мережі Петрі можна значно розширити, якщо маркерам призначати різні типи даних, наприклад рядки символів, цілі або дійсні числа, множини, структури, як це робиться в мовах програмування. Тоді у разі зображення вузлів з такими маркерами необхідно вказувати типи даних і визначати максимальну кількість маркерів кожного типу, які можуть знаходитись у вузлі. Існує ще одна можливість розширення функцій вузлів - зазначити режим доступу до маркерів, тобто задати, яким чином маркери(дані) надходять до вузлів та як вони в них вилучаються. Це дає змогу формувати у вузлах черги маркерів подібно тому, чк створюються черги вимог у СМО. У Табл.1 наведено основні режими доступу до вузлів.

Табл.1 Основні режими доступу до вузлів у рожширеннях мереж Петрі.

Режим доступу Опис
RAM Принцип випадкового доступу. Маркер, який надійшов до вузла, розміщується в черзі випадково. У разі спрацювання переходу маркер, який вилучается з черги, вибирається випадково.
FIFO Принцип "перший прийшов-перший пішов". Маркер, який надійшов до вузла, розміщується в черзі останнім. У разі спрацювання переходу вилучаеться перший маркер черги.
LIFO Принцип "останній прийшов-перший пішов". Маркер, який надійшов до вузла останнім, розміщується в черзі першим. У разі спрацювання переходу вилучається перший маркер.
FIFORAM Принцип "прийшов випадково - перший покинув". Маркер, який надійшов, розміщується в черзі випадково. У разі спрацювання переходу з черги вилучається перший маркер.
LIFORAM Принцип "прийшов випадково - останній покинув". Маркер, який надійшов, розміщується в черзі випадково. У разі спрацювання переходу з черги вилучаеться перший маркер.

Вибір режимів формування черги і вилучення із неї маркерів залежить від того, в якій послідовності потрібно перевіряти маркери у вузлах. Тому навряд чи можна дати загальну пораду відносно того, які режими доступу використовувати. У простих мережах Петрі автоматичного використовується режим довільного доступу (порядок поставлення маркерів у чергу та порядок їх вилучення для них не має значення). Розширення можливостей вузлів мереж Петрі є досить зручним засобом для моделювання матеріальних та інформаційних потоків у виробничих системах.

Дослідження мережі Петрі

Основні методи дослідження мереж Петрі:

  1. Дерево досягальності,
  2. Графічний,
  3. Аналітичний,
  4. За допомогою еквівалентних перетвореннь.

Взагалі, мережі Петрі досліджують на такі властивості:

  1. Безпечність — досліджує виконання умови що кількість «фішок» в позиції не перевищує 1;
  2. Обмеженість — досліджує виконання умови що кількість «фішок» в позиції не перевищує заданого числа,
  3. Зберігальність — досліджує виконання умови що кількість «фішок» в мережі не змінюється,
  4. Оберненість — для довільного досяжного стану досліджується існування послідовності виконань переходів яка повертає мережу в початковий стан),
  5. Активність переходів — досліджує можливість виконання певних переходів та наявність тупиків — станів у яких переходи не дозволені та для яких неможливо досягти стану в якому ці переходи дозволені,
  6. Досяжність маркування — досліджує існування послідовності виконань переходів при якій можна досягнути задане маркування,
  7. Покриття — досліджує існування послідовності виконань переходів при якій можна досягнути маркування що покриває, тобто є більшим за задане маркування.

Умова зберігальності може бути послаблена, для чого вводять поняття функції ваги, яка залишається постійною під час роботи.

Неможливо розібрати вираз (невідома помилка): \mathbf W:\qquad(\mathbf T \times \mathbf P) \cup (\mathbf P \times \mathbf T) \to \mathbb N \cup \{0\}


Види мереж Петрі

Деякі види мереж Петрі:

  • Тимчасова мережа Петрі - переходи мають вагою, визначаючу тривалість спрацьовування (затримку).
  • Стохастична мережа Петрі - затримки є випадковими величинами.
  • Функціональна мережа Петрі - затримки визначаються як функції деяких аргументів, наприклад, кількості міток в будь-яких позиціях, стану деяких переходів.
  • Кольорова мережа Петрі - мітки можуть бути різних типів, які позначені різними кольорами, тип мітки може бути використаний як аргумент у функціональних мережах.
  • Інгібіторна мережа Петрі - можливі інгібіторні дуги, що забороняють спрацьовування переходу, якщо у вхідній позиції знаходиться мітка.
  • Ієрархічна мережа - містить не миттєві переходи, в які вкладено інші, можливо, також ієрархічні мережі. Спрацювання такого переходу характеризує виконання повного життєвого циклу вкладеної мережі.
  • WF-мережі

Проблеми розв’язності мереж Петрі

На даний час існують такі проблеми розв’язності для мереж Петрі:

1. Проблема досяжності (тупикової) розмітки.

2. Проблема досяжності переходу.

3. Проблема життєвості.

4. Проблема еквівалентність.

5. Проблема рівності.

6. Проблема k-обмеженості.

7. Проблема обмеженості.


Комп'ютерні моделюючі системи

1. Pndpi

2. Tina

3. Design/CPN

4. HPSim

Список використаної літератури

  1. Зайцев Д.А. Мережі Петрі і моделювання систем: Навчальній посібник // , Одеса 2006
  2. Зайцев Д.А. Математичні моделі дискретних систем: Навчальний посібник // Одеса: ОНАЗ ім. О.С. Попова, 2004. – 40 с.
  3. Математичні основи теорії телекомунікаційних систем / Підручник за загальною редакцію В.В. Поповського. – Харків, ТОВ «Компанія СМІТ», 2006. – 564 с.
  4. Питерсон Дж. Теория сетей Петри и моделирование систем. – М. Мир, 1984. – 264 с.
  5. Котов В.Е. Сети Петри. – М.: Наука, 1984. – 160 с.
  6. Ачасова С.М., Бандман О.Л. Корректность параллельных вычислительных процессов. – Н.: Наука, 1990. – 253 с.
  7. Слепцов А.И., Юрасов А.А. Автоматизация проектирования управляющих систем гибких автоматизированных производств / Под ред. Б.Н.Малиновского. – К.: Технiка, 1986. – 160 с.
Отримано з https://wiki.cusu.edu.ua/index.php?title=Мережі_Петрі&oldid=97564