Відмінності між версіями «Використання кривих Безьє»

Матеріал з Вікі ЦДУ
Перейти до: навігація, пошук
 
(не показані 23 проміжні версії цього учасника)
Рядок 1: Рядок 1:
−
'''Викристання кривих Безьє у векторній графіці'''
+
'''Використання кривих Безьє у векторній графіці'''
 +
 
 +
[[Файл:Крива Безьє.png|макс]]
 +
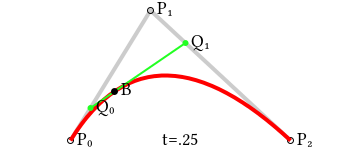
        Крива Безьє
  
 
Криві Безьє зустрічаються як в растровій так і в векторній графіці. Всі комп’ютерні шрифти складаються з цих кривих. В Photoshop використовується термін контур, що базується на кривих Безьє. Цей інструмент виділяє на рисунку потрібний для вирізання об’єкт.  
 
Криві Безьє зустрічаються як в растровій так і в векторній графіці. Всі комп’ютерні шрифти складаються з цих кривих. В Photoshop використовується термін контур, що базується на кривих Безьє. Цей інструмент виділяє на рисунку потрібний для вирізання об’єкт.  
−
Наборами кривих Безьє можна апроксимувати будь-який складний контур. Щоб не було зломів треба з допомогою функції згладжування (smooth) привести точки сусідніх відрізків в одну лінію, після чого злом зникне.
+
Наборами кривих Безьє можна апроксимувати будь-який складний контур. Щоб не було зломів треба з допомогою функції згладжування (smooth) привести точки сусідніх відрізків в одну лінію, після чого злом зникне.Застосування кривих Безьє дозволило реалізувати управління рухом комп’ютерного персонажу. Тому, ці криві використовуються не тільки в двохмірній графіці, а й в трьохмірній,  
−
Застосування кривих Безьє дозволило реалізувати управління рухом комп’ютерного персонажу. Тому, ці криві використовуються не тільки в двохмірній графіці, а й в трьохмірній, відео, анімації.
+
відео, анімації.
  
 +
                                                                                                                                               
 
''Властивості кривої Безьє:''
 
''Властивості кривої Безьє:''
−
# безперервність заповнення сегмента між початковою та кінцевою точками;
+
 
−
# крива завжди розташовується всередині фігури, утвореної лініями, що з'єднують контрольні точки;
+
{| class="wikitable" border="1"
−
# при наявності лише двох контрольних точок сегмент являє собою пряму лінію;
+
|-
−
# пряма лінія утворюється лише тоді, коли контрольні точки розташовані на одній прямій;
+
! №
−
# крива Безьє симетрична, тобто обмін місцями між початковою та кінцевою точками (зміна напрямку траєкторії) не впливає на форму кривої;
+
! Властивість
−
# масштабування та зміна пропорцій кривої Безьє не порушує її стабільності, оскільки вона з математичної точки зору «аффінно інваріантна»;
+
|-
−
# зміна координат хоча б однієї з точок веде до зміни форми всієї кривої Безьє;
+
| 1
−
# будь який частковий відрізок кривої Безьє також є кривою Безьє;
+
| безперервність заповнення сегмента між початковою та кінцевою точками.
−
# степінь кривої завжди на одиницю менший від кількості контрольних точок. Наприклад, при трьох контрольних точках форма кривої — парабола;
+
|-
−
# коло не може бути описане параметричним рівнянням кривої Безьє;
+
| 2
−
# неможливо створити паралельні криві Безьє, за винятком тривіальних випадків (прямі лінії та однакові криві), хоча існують алгоритми, що будують наближену паралельну криву Безьє з прийнятною для практики точністю.
+
| крива завжди розташовується всередині фігури, утвореної лініями, що з'єднують контрольні точки.
 +
|-
 +
| 3
 +
| при наявності лише двох контрольних точок сегмент являє собою пряму лінію.
 +
|-
 +
| 4
 +
| пряма лінія утворюється лише тоді, коли контрольні точки розташовані на одній прямій.
 +
|-
 +
| 5
 +
| крива Безьє симетрична, тобто обмін місцями між початковою та кінцевою точками (зміна напрямку траєкторії) не впливає на форму кривої.
 +
|-
 +
| 6
 +
| масштабування та зміна пропорцій кривої Безьє не порушує її стабільності, оскільки вона з математичної точки зору «аффінно інваріантна».
 +
|-
 +
|7
 +
| зміна координат хоча б однієї з точок веде до зміни форми всієї кривої Безьє.
 +
|-
 +
| 8
 +
| будь який частковий відрізок кривої Безьє також є кривою Безьє.
 +
|-
 +
| 9
 +
| степінь кривої завжди на одиницю менший від кількості контрольних точок. Наприклад, при трьох контрольних точках форма кривої — парабола.
 +
|-
 +
| 10
 +
| коло не може бути описане параметричним рівнянням кривої Безьє.
 +
|-
 +
| 11
 +
| неможливо створити паралельні криві Безьє, за винятком тривіальних випадків (прямі лінії та однакові криві), хоча існують алгоритми, що будують наближену паралельну криву Безьє з прийнятною для практики точністю.
 +
|}
 +
 
  
 
Завдяки простоті завдання і виконанню операцій, криві Безьє знайшли широке застосування в комп'ютерній графіці для моделювання гладких ліній. Крива цілком лежить в опуклій оболонці своїх опорних точок. Ця властивість кривих Безьє з одного боку значно полегшує завдання знаходження точок перетину кривих (якщо не перетинаються опуклі оболонки опорних точок, то не перетинаються і самі криві), а з іншого боку дозволяє здійснювати інтуїтивно зрозуміле управління параметрами кривої в графічному інтерфейсі за допомогою її опорних точок. Крім того, афінні перетворення кривої (перенесення, масштабування, обертання та ін.) також можуть бути виконані через застосування відповідних перетворень до опорних точок.
 
Завдяки простоті завдання і виконанню операцій, криві Безьє знайшли широке застосування в комп'ютерній графіці для моделювання гладких ліній. Крива цілком лежить в опуклій оболонці своїх опорних точок. Ця властивість кривих Безьє з одного боку значно полегшує завдання знаходження точок перетину кривих (якщо не перетинаються опуклі оболонки опорних точок, то не перетинаються і самі криві), а з іншого боку дозволяє здійснювати інтуїтивно зрозуміле управління параметрами кривої в графічному інтерфейсі за допомогою її опорних точок. Крім того, афінні перетворення кривої (перенесення, масштабування, обертання та ін.) також можуть бути виконані через застосування відповідних перетворень до опорних точок.
Рядок 22: Рядок 55:
 
Найбільше значення мають криві Безьє другого та третього ступенів (квадратичні і кубічні). Криві вищих ступенів при обробці вимагають більшого обсягу обчислень і для практичних цілей використовуються рідше. Для побудови складних за формою ліній, окремі криві Безьє можуть бути послідовно з'єднані один з одним в сплайн Безьє. Для того, щоб забезпечити гладкість лінії в місці з'єднання двох кривих, три суміжні опорні точки обох кривих повинні лежати на одній прямій. У програмах векторної графіки на зразок Adobe Illustrator або Inkscape подібні фрагменти відомі під назвою «шляхів» (path).
 
Найбільше значення мають криві Безьє другого та третього ступенів (квадратичні і кубічні). Криві вищих ступенів при обробці вимагають більшого обсягу обчислень і для практичних цілей використовуються рідше. Для побудови складних за формою ліній, окремі криві Безьє можуть бути послідовно з'єднані один з одним в сплайн Безьє. Для того, щоб забезпечити гладкість лінії в місці з'єднання двох кривих, три суміжні опорні точки обох кривих повинні лежати на одній прямій. У програмах векторної графіки на зразок Adobe Illustrator або Inkscape подібні фрагменти відомі під назвою «шляхів» (path).
 
Метод побудови кривих Безьє базується на застосуванні пари дотичних проведених до лінії в точках її закінчення.
 
Метод побудови кривих Безьє базується на застосуванні пари дотичних проведених до лінії в точках її закінчення.
−
      - Лугова Анастасія МІ19Б
+
 
 +
                                                                    - Лугова Анастасія МІ19Б

Поточна версія на 13:33, 9 листопада 2020

Використання кривих Безьє у векторній графіці

макс 

       Крива Безьє

Криві Безьє зустрічаються як в растровій так і в векторній графіці. Всі комп’ютерні шрифти складаються з цих кривих. В Photoshop використовується термін контур, що базується на кривих Безьє. Цей інструмент виділяє на рисунку потрібний для вирізання об’єкт. Наборами кривих Безьє можна апроксимувати будь-який складний контур. Щоб не було зломів треба з допомогою функції згладжування (smooth) привести точки сусідніх відрізків в одну лінію, після чого злом зникне.Застосування кривих Безьє дозволило реалізувати управління рухом комп’ютерного персонажу. Тому, ці криві використовуються не тільки в двохмірній графіці, а й в трьохмірній, відео, анімації.


Властивості кривої Безьє:

№ Властивість
1 безперервність заповнення сегмента між початковою та кінцевою точками.
2 крива завжди розташовується всередині фігури, утвореної лініями, що з'єднують контрольні точки.
3 при наявності лише двох контрольних точок сегмент являє собою пряму лінію.
4 пряма лінія утворюється лише тоді, коли контрольні точки розташовані на одній прямій.
5 крива Безьє симетрична, тобто обмін місцями між початковою та кінцевою точками (зміна напрямку траєкторії) не впливає на форму кривої.
6 масштабування та зміна пропорцій кривої Безьє не порушує її стабільності, оскільки вона з математичної точки зору «аффінно інваріантна».
7 зміна координат хоча б однієї з точок веде до зміни форми всієї кривої Безьє.
8 будь який частковий відрізок кривої Безьє також є кривою Безьє.
9 степінь кривої завжди на одиницю менший від кількості контрольних точок. Наприклад, при трьох контрольних точках форма кривої — парабола.
10 коло не може бути описане параметричним рівнянням кривої Безьє.
11 неможливо створити паралельні криві Безьє, за винятком тривіальних випадків (прямі лінії та однакові криві), хоча існують алгоритми, що будують наближену паралельну криву Безьє з прийнятною для практики точністю.


Завдяки простоті завдання і виконанню операцій, криві Безьє знайшли широке застосування в комп'ютерній графіці для моделювання гладких ліній. Крива цілком лежить в опуклій оболонці своїх опорних точок. Ця властивість кривих Безьє з одного боку значно полегшує завдання знаходження точок перетину кривих (якщо не перетинаються опуклі оболонки опорних точок, то не перетинаються і самі криві), а з іншого боку дозволяє здійснювати інтуїтивно зрозуміле управління параметрами кривої в графічному інтерфейсі за допомогою її опорних точок. Крім того, афінні перетворення кривої (перенесення, масштабування, обертання та ін.) також можуть бути виконані через застосування відповідних перетворень до опорних точок.

Найбільше значення мають криві Безьє другого та третього ступенів (квадратичні і кубічні). Криві вищих ступенів при обробці вимагають більшого обсягу обчислень і для практичних цілей використовуються рідше. Для побудови складних за формою ліній, окремі криві Безьє можуть бути послідовно з'єднані один з одним в сплайн Безьє. Для того, щоб забезпечити гладкість лінії в місці з'єднання двох кривих, три суміжні опорні точки обох кривих повинні лежати на одній прямій. У програмах векторної графіки на зразок Adobe Illustrator або Inkscape подібні фрагменти відомі під назвою «шляхів» (path). Метод побудови кривих Безьє базується на застосуванні пари дотичних проведених до лінії в точках її закінчення. 

                                                                   - Лугова Анастасія МІ19Б
Отримано з https://wiki.cusu.edu.ua/index.php?title=Використання_кривих_Безьє&oldid=370999