Відмінності між версіями «Сейсморозвідка і суперкомп`ютер»
4596645 (обговорення • внесок) |
4596645 (обговорення • внесок) |
||
| (не показано одну проміжну версію цього учасника) | |||
| Рядок 54: | Рядок 54: | ||
дискретной свертки одномерных массивов, каждый из которых состоит из 2000 элементов. Трафик данных составляет более одного петабайта. Если бы мы доверили вычисления одному единственному, пусть самому быстрому, серверу, то получили бы результат через три года. С практической точки зрения это | дискретной свертки одномерных массивов, каждый из которых состоит из 2000 элементов. Трафик данных составляет более одного петабайта. Если бы мы доверили вычисления одному единственному, пусть самому быстрому, серверу, то получили бы результат через три года. С практической точки зрения это | ||
лишено всякого смысла. Однако при использовании лишь пятой части суперкомпьютера “Ломоносов” для | лишено всякого смысла. Однако при использовании лишь пятой части суперкомпьютера “Ломоносов” для | ||
| − | получения результатов хватило бы трех дней. На рис. | + | получения результатов хватило бы трех дней. На рис. 3 приведены сейсмические разрезы по исходным |
данным (а) и по результату подавления кратных волн-помех (1). Здесь нам удалось добиться высокого | данным (а) и по результату подавления кратных волн-помех (1). Здесь нам удалось добиться высокого | ||
качества подавления помехи. Следующий важный класс алгоритмов посвящен построению глубинного сейсмического изображения | качества подавления помехи. Следующий важный класс алгоритмов посвящен построению глубинного сейсмического изображения | ||
| Рядок 68: | Рядок 68: | ||
И наконец, посредством корреляции этих полей получают глубинное изображение среды. Очевидно, что | И наконец, посредством корреляции этих полей получают глубинное изображение среды. Очевидно, что | ||
для быстрой работы алгоритма необходимо наличие быстрых жестких дисков на каждом вычислительном узле. Этот метод требует значительно б´ольших вычислительных затрат по сравнению с предыдущим, | для быстрой работы алгоритма необходимо наличие быстрых жестких дисков на каждом вычислительном узле. Этот метод требует значительно б´ольших вычислительных затрат по сравнению с предыдущим, | ||
| − | однако в ряде случаев дает лучший результат. В работе [2] (см. рис. | + | однако в ряде случаев дает лучший результат. В работе [2] (см. рис. 4)[[Файл:Рис._8._Подавление_кратных_волн-помех.PNG|thumb|Рис. 3. Подавление кратных волн-помех методом 3D SRME (по [8] с изменениями)]] [[Файл:Рис._9._Построение_глубинного_изображения.PNG|thumb| Рис. 4. Построение глубинного изображения среды различными методами (по [2] с изменениями)]]приведен пример сравнения результатов, полученных при использовании обоих описанных алгоритмов для сложных данных из района с |
соляно-купольной тектоникой. Здесь целью являлось построение глубинного изображения соляного тела | соляно-купольной тектоникой. Здесь целью являлось построение глубинного изображения соляного тела | ||
| − | с “карнизом”, а также примыкающих к нему слоев осадочных отложений. На рис. | + | с “карнизом”, а также примыкающих к нему слоев осадочных отложений. На рис. 4а приводится результат миграции методом Кирхгофа, а на рис. 4б — результат миграции в обратном времени. В областях с |
номером 1 оба метода дают приемлемое качество изображения, а области с номером 2 — это зона, где | номером 1 оба метода дают приемлемое качество изображения, а области с номером 2 — это зона, где | ||
конфигурацию соляного тела можно получить только при помощи времяемкого алгоритма миграции в | конфигурацию соляного тела можно получить только при помощи времяемкого алгоритма миграции в | ||
| Рядок 103: | Рядок 103: | ||
6.Margrave G.F. Numerical methods in exploration seismology with algorithms in MATLAB. 2003 | 6.Margrave G.F. Numerical methods in exploration seismology with algorithms in MATLAB. 2003 | ||
(www.crewes.org/ResearchLinks/FreeSoftware/EduSoftware/NumMeth.pdf). | (www.crewes.org/ResearchLinks/FreeSoftware/EduSoftware/NumMeth.pdf). | ||
| − | 7 | + | 7.Курин Е.А. О производительности компьютеров для обработки данных сейсморазведки // Технологии сейсморазведки. 2007. № 4. 69–76. |
| − | + | ||
| − | + | ||
| − | + | ||
Поточна версія на 11:47, 29 грудня 2018
Зміст
Сейсморазведка и суперкомпьютеры
При поисках, разведке и разработке нефтяных и газовых месторождений применяются математические методы, требующие большого объема вычислений в достаточно сжатые сроки. Здесь мы остановимся на задачах обработки данных, полученных при сейсмической разведке, так как именно они предъявляют самые высокие требования к объему вычислений. Разумеется, в отрасли существуют и другие области применения высокопроизводительных вычислений, например моделирование углеводородных систем в осадочных бассейнах, а также гидродинамическое моделирование в процессе добычи. В работе приводится сопоставление различных методов построения глубинного изображения среды по сейсмическим данным и необходимых вычислительных ресурсов. Там показано, что применение ряда эффективных процедур в экономически оправданные сроки требует применения суперкомпьютеров. Поэтому неудивительно, что высокопроизводительные вычисления в области сейсморазведки в настоящее время являются актуальной темой исследований специалистов нефтегазовых и сервисных компаний и академических организаций. В рамках каждой международной геофизической конференции (SEG, EAGE) проводятся соответствующие сессии или семинары. Организуются и специализированные мероприятия, например ежегодный семинар в Rice University (г. Хьюстон, США), посвященный высокопроизводительным вычислениям в нефтяной и газовой отрасли. Увеличилось количество публикаций на данную тему в геолого-геофизических периодических изданиях. В настоящей статье дано краткое описание сейсмического метода поисков полезных ископаемых, сделан обзор задач и методов обработки сейсмических данных, а также рассмотрены отдельные процедуры, требующие применения высокопроизводительных вычислительных систем.
О сейсморазведке
Нефть и газ сосредоточены в так называемых ловушках. Они представляют собой участки пористых и проницаемых пород, в которых происходит накопление углеводородов. Эти породы перекрываются другими, непроницаемыми, породами, которые препятствуют дальнейшей миграции нефти и газа. Одной из основных задач сейсморазведки является поиск и определение пространственного положения глубинных структур, которые могли бы являться такими ловушками. Не менее важно построение геологической модели по всему месторождению для того, чтобы оптимальным образом осуществлять его разработку, сведя к минимуму технологические и экологические риски. Напомним основы сейсмического метода. Вблизи поверхности Земли искусственно возбуждают упругие волны, которые распространяются в нижнее полупространство. Часть из них, претерпев отражение и преломление на границах раздела горных пород, возвращается к поверхности. Здесь происходит их регистрация специальными устройствами — сейсмоприемниками. На акваториях процесс наблюдений происходит следующим образом: судно буксирует периодически срабатывающий источник и кабели, так называемые “косы”, с приемниками (гидрофонами). На суше обычно применяют взрывные или вибрационные источники и стационарно размещенные приемники (геофоны), для которых обеспечивается механический контакт с поверхностью наблюдений
Суперкомпьютеры и некоторые задачи обработки данных
С момента своего появления компьютеры стали применяться при обработке сейсмических данных. Однако, несмотря на бурный рост возможностей вычислительной техники в последние десятилетия, оказывается, что эти возможности отстают от потребностей сейсморазведки. Например, в 2009 г. на месторождении Карачаганак (Казахстан) проводились трехмерные наблюдения на площади около 900 кв. км. При этом были зарегистрированы около трех миллиардов записей (трасс). Общий объем данных превысил 100 терабайт. Если мы попытаемся прочитать такой объем данных с внешних USBдисков на компьютер, то процесс чтения займет полтора месяца. Кроме того, данные надо еще обработать и записать результат обработки, что также потребует значительного времени. В настоящее время ни одна нефтяная компания не согласна ждать результата так долго, и необходимо применять более совершенные устройства для вычислений и хранения данных. Рассмотрим, как обрабатываются данные при помощи стандартного набора процедур, в который обычно входят модули для работы с геометрией наблюдений и подавления регулярных и нерегулярных помех. Такие процедуры применяются последовательно к небольшим порциям данных, которые передаются по конвейеру. Отдельные порции данных обрабатываются независимо друг от друга. Для этого класса задач узким местом является подсистема ввода-вывода. Поэтому идеальным компьютером для их решения будет кластер с узлами, обладающими быстрым доступом к общей системе хранения данных (СХД).Изучим, как эта проблема может быть решена на современных суперкомпьютерах, установленных
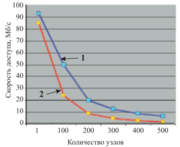
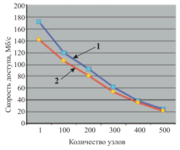
в Московском государственном университете им. М. В. Ломоносова. На рис. 1 изображены результатыизмерения скорости чтения и записи данных одним узлом в зависимости от количества одновременно читающих и пишущих узлов для суперкомпьютера “Чебышев”. Нетрудно посчитать, что, например, 200 узлов могут прочитать 100 терабайт за 8 часов. На рис. 2 приведены аналогичные измерения для новейшего суперкомпьютера “Ломоносов”, также установленного в МГУ. Время чтения 100 терабайт данных уменьшилось еще в три раза. Далее мы остановимся на некоторых отдельных процедурах, требующих большого объема вычислений. Известно, что при обработке сейсмических данных, полученных на акваториях, остро стоит проблема подавления кратных волн-помех. Кратные волны образуются при многократном отражении от границ раздела горных пород, часто с участием отражения от дневной поверхности, и они затрудняют интерпретацию полезных волн. При подавлении таких помех применяются различные методы, например основанные на каких-либо отличиях в свойствах полезных волн и помех. Одним из самых эффективных способов подавления кратных волн является метод SRME (Surface-Related Multiple Elimination), предложенный профессором Беркхаутом из Делфтского университета в Нидерландах. Метод двухшаговый. На первом шаге делается прогнозирование помехи, а на втором — ее адаптивное вычитание. Для прогнозирования одной трассы помехи производится попарная свертка трасс сейсмограмм общих пунктов взрыва и приема, к которым принадлежит эта трасса, в пределах некоторой апертуры. На втором шаге производится поиск многоканального фильтра, который оптимальным образом адаптирует оценку помехи к реальным данным. После применения фильтра помеха вычитается из данных. В двумерном, а особенно в трехмерном, случае мы имеем значительный объем как ввода-вывода, так и вычислений. Рассмотрим пример применения метода 3D SRME для морских широкоазимутальных данных по площади 400 кв. км и размером порядка 1 терабайта. В процессе вычислений производится около 100 миллиардов операций дискретной свертки одномерных массивов, каждый из которых состоит из 2000 элементов. Трафик данных составляет более одного петабайта. Если бы мы доверили вычисления одному единственному, пусть самому быстрому, серверу, то получили бы результат через три года. С практической точки зрения это лишено всякого смысла. Однако при использовании лишь пятой части суперкомпьютера “Ломоносов” для получения результатов хватило бы трех дней. На рис. 3 приведены сейсмические разрезы по исходным данным (а) и по результату подавления кратных волн-помех (1). Здесь нам удалось добиться высокого качества подавления помехи. Следующий важный класс алгоритмов посвящен построению глубинного сейсмического изображения среды по данным и по предварительно оцененной глубинно-скоростной модели. Этот процесс называется сейсмической миграцией. Самым простым, интуитивно понятным и быстрым является метод, основанный на вычислении приближения к интегралу Кирхгофа. С вычислительной точки зрения он сводится к суммированию отсчетов входных данных вдоль некоторой траектории, зависящей от скорости в среде. Таким образом, для получения одного отсчета результата необходим доступ к значительной части данных. При этом размер данных может быть порядка нескольких терабайт. Идеальный компьютер для решения этой задачи — с общей памятью, вмещающей входные данные и результат интегрирования. Возможно эффективное решение задачи на кластере с быстрой коммуникационной сетью, где организовано оптимальное размещение входных данных в распределенном массиве. Альтернативный метод построения глубинного изображения — это миграция в обратном времени (reverse time migration, RTM). Для каждого пункта взрыва моделируется и запоминается на диске волновое поле во все моменты времени в пределах интервала записи данных. Затем для соответствующей этому пункту взрыва сейсмограммы производится продолжение волнового поля, зарегистрированного на поверхности, в обратном времени. Это также делается во все моменты времени в пределах интервала записи. И наконец, посредством корреляции этих полей получают глубинное изображение среды. Очевидно, что для быстрой работы алгоритма необходимо наличие быстрых жестких дисков на каждом вычислительном узле. Этот метод требует значительно б´ольших вычислительных затрат по сравнению с предыдущим,
однако в ряде случаев дает лучший результат. В работе [2] (см. рис. 4) приведен пример сравнения результатов, полученных при использовании обоих описанных алгоритмов для сложных данных из района ссоляно-купольной тектоникой. Здесь целью являлось построение глубинного изображения соляного тела с “карнизом”, а также примыкающих к нему слоев осадочных отложений. На рис. 4а приводится результат миграции методом Кирхгофа, а на рис. 4б — результат миграции в обратном времени. В областях с номером 1 оба метода дают приемлемое качество изображения, а области с номером 2 — это зона, где конфигурацию соляного тела можно получить только при помощи времяемкого алгоритма миграции в обратном времени. В обоих случаях время вычислений составляет около двух недель. Однако если для получения результата при помощи миграции Кирхгофа достаточно кластера с 32 узлами, то для миграции в обратном времени требуется суперкомпьютер с сотнями вычислительных узлов. Ряд задач обработки сейсмических данных подразумевает то, для чего современные суперкомпьютеры общего назначения, собственно, и спроектированы: решение систем линейных алгебраических уравнений большой размерности. К таким задачам можно отнести, в первую очередь, определение статических поправок для площадных (3D) данных. Статические поправки представляют собой временн ´ые задержки, связанные с рельефом дневной поверхности и неоднородностями верхней части разреза. Качество определения и учета статических поправок непосредственно влияет как на надежность выделения и корреляцию отраженных волн, так и на достоверность последующих глубинных построений. Наличие статических сдвигов препятствует синфазному суммированию полезных волн. Для решения этой задачи предложено много методов, более или менее эффективных в различных условиях. Многие из них сводятся к решению системы линейных алгебраических уравнений, размерность которых зачастую превышает произведение количества пунктов взрыва и количества пунктов приема, используемых в процессе наблюдений на исследуемой площади. При этом такая система, как правило, вырожденная, и ее решение может осуществляться методом наименьших квадратов. Для уменьшения размера оперативной памяти, требуемой для решения, используются некоторые свойства системы уравнений, в частности разреженность и характерная блочная структура. К системам линейных алгебраических уравнений также приводят другие задачи, например различные томографические методы оценки глубинно-скоростной модели среды по временам пробега отраженных волн, сейсмическое моделирование и полноволновая инверсия (full-waveform inversion, FWI) в частотной области. Следует также упомянуть о нестандартных вычислительных технологиях, используемых при работе с сейсмическими данными. В настоящее время наблюдается большой интерес разработчиков к различного рода аппаратным ускорителям. В частности, опубликован ряд работ по использованию графических процессоров общего назначения (GPU) для решения отдельных задач сейсмического моделирования и построения глубинных изображений. При этом обычно применяется технология CUDA, разрабатываемая и продвигаемая компанией NVidia. Распространение этой технологии на более широкий класс задач сдерживается особенностями архитектуры графических процессоров и ограничениями производительности интерфейса PCI-E, служащего для соединения плат ускорителей с материнской вычислительной системой. Кроме того, существуют работы по оптимизации ряда алгоритмов обработки для ускорителей на основе ПЛИС (FPGA).
Список Литературы
1.Camp W.J, Thierry P. Trends for high-performance scientific computing // The Leading Edge. 2010. 29. 44–47. 2.Suh S.Y., Yeh A., Wang B., Cai J., Yoon K., Li Z. Cluster programming for reverse time migration // The Leading Edge. 2010. 29. 94–97. 3.Материалы семинара по высокопроизводительным вычислениям в нефтяной и газовой отрасли (www.og-hpc.org). 4.Шерифф Р., Гелдарт Л. Сейсморазведка. М.: Мир, 1987. 5.Вычислительные математика и техника в разведочной геофизике. Справочник геофизика / Под ред. В. И. Дмитриева. М.: Недра, 1982. 6.Margrave G.F. Numerical methods in exploration seismology with algorithms in MATLAB. 2003 (www.crewes.org/ResearchLinks/FreeSoftware/EduSoftware/NumMeth.pdf). 7.Курин Е.А. О производительности компьютеров для обработки данных сейсморазведки // Технологии сейсморазведки. 2007. № 4. 69–76.