Відмінності між версіями «Стаття проекту "Урок майбутнього!" Новоскольцева Анна»
2419159 (обговорення • внесок) |
2419159 (обговорення • внесок) |
||
| (не показано 5 проміжних версій цього учасника) | |||
| Рядок 14: | Рядок 14: | ||
Властивості і графіки функцій y=sin x і y=cos x | Властивості і графіки функцій y=sin x і y=cos x | ||
===Тип уроку=== | ===Тип уроку=== | ||
| − | + | *Урок застосування знань, умінь і навичок; | |
| − | *Урок | + | *Інтегрований (математика-інформатика) |
| − | *Інтегрований (математика-інформатика) | + | |
==Мета уроку== | ==Мета уроку== | ||
| Рядок 29: | Рядок 28: | ||
''Технологія «Цікавий факт»<br> | ''Технологія «Цікавий факт»<br> | ||
| − | У фізиці вивчення механічних та електромагнітних коливань і хвиль тісно пов’язано з поняттям тригонометричних функцій. Адже ці коливання здійснюються за законом синуса або косинуса. Вони дають можливість глибше зрозуміти природу навколишнього світу | + | У фізиці вивчення механічних та електромагнітних коливань і хвиль тісно пов’язано з поняттям тригонометричних функцій. Адже ці коливання здійснюються за законом синуса або косинуса. Вони дають можливість глибше зрозуміти природу навколишнього світу. <br> |
| − | + | ||
Графіком коливань математичного маятника є синусоїда. | Графіком коливань математичного маятника є синусоїда. | ||
| + | Осцилограф. | ||
[[Файл:Осцилограф.jpg |300 px| center]] | [[Файл:Осцилограф.jpg |300 px| center]] | ||
Сьогодні у нас незвичний урок – ми навчимось будувати графіки тригонометричних функцій, а перевіряти будемо за допомогою комп’ютера.'' | Сьогодні у нас незвичний урок – ми навчимось будувати графіки тригонометричних функцій, а перевіряти будемо за допомогою комп’ютера.'' | ||
| Рядок 138: | Рядок 137: | ||
#Тест для перевірки знань учнів [https://docs.google.com/forms/d/e/1FAIpQLSejBCgf79dWy_JZadG7DKtyB7EgQkX9O6MFYhHlwlr4thJb8A/viewform?usp=sf_link Тест] | #Тест для перевірки знань учнів [https://docs.google.com/forms/d/e/1FAIpQLSejBCgf79dWy_JZadG7DKtyB7EgQkX9O6MFYhHlwlr4thJb8A/viewform?usp=sf_link Тест] | ||
#Ментальні карти [https://mm.tt/1106412150?t=FnQia258KE Ментальні карти] | #Ментальні карти [https://mm.tt/1106412150?t=FnQia258KE Ментальні карти] | ||
| − | #Ігра для учнів | + | #Ігра для учнів [https://learningapps.org/display?v=p0ja1zdd318 Значення тригонометричних функцій] |
| − | #Публікація або інфографіка [https://www.canva.com/design/DAC5nFqrgPQ/ | + | #Публікація або інфографіка [https://www.canva.com/design/DAC5nFqrgPQ/view Публікація] |
#Електронний журнал [https://docs.google.com/spreadsheets/d/1ApjeUYnLna_1FESeL7PRjfEn8vbcWS3lnyC5pAFX410/edit#gid=395504598 Журнал] | #Електронний журнал [https://docs.google.com/spreadsheets/d/1ApjeUYnLna_1FESeL7PRjfEn8vbcWS3lnyC5pAFX410/edit#gid=395504598 Журнал] | ||
#Методичні або дидактичні матеріали до уроку [https://www.geogebra.org/m/GHCa8g9g Перетворення синуса] | #Методичні або дидактичні матеріали до уроку [https://www.geogebra.org/m/GHCa8g9g Перетворення синуса] | ||
Поточна версія на 10:00, 5 червня 2018
Зміст
- 1 Навчальний предмет
- 2 Тема уроку
- 3 Хід уроку
- 3.1 1. Повідомлення теми, мети і завдань уроку, мотивація учіння школярів.
- 3.2 2. Перевірка домашнього завдання, повторення раніше вивченого матеріалу.
- 3.3 3. Актуалізація суб’єктивного досвіду і опорних знань
- 3.4 4. Вивчення нового матеріалу (вступні, мотиваційні та пізнавальні вправи).
- 3.5 5. Підсумки уроку.
- 3.6 6. Повідомлення домашнього завдання.
- 4 Методичні та дидактичні матеріали
- 5 Інформаційні ресурси
Навчальний предмет
Алгебра
Вік учнів, клас
15-16 років, 10 клас
Тема уроку
Властивості і графіки функцій y=sin x і y=cos x
Тип уроку
- Урок застосування знань, умінь і навичок;
- Інтегрований (математика-інформатика)
Мета уроку
Навчальна мета формувати в учнів навички побудови графіків тригонометричних функцій, що містять синус та косинус на основі перетворень відомих графіків y= sin x, y= cos x;
Розвивальна мета розвивати вміння аналізувати, порівнювати й узагальнювати навчальний матеріал; сприяти формуванню причинно-наслідкових зв’язків;
Виховна мета виховувати почуття поваги до навчання; створити ситуацію успіху для кожного учня.
Хід уроку
1. Повідомлення теми, мети і завдань уроку, мотивація учіння школярів.
Технологія «Цікавий факт»
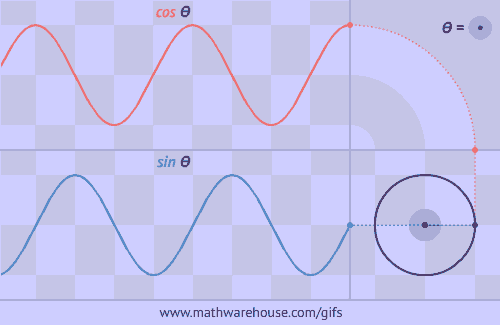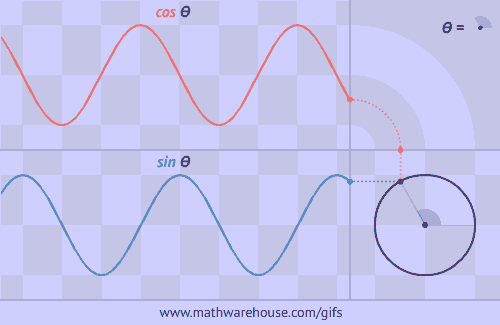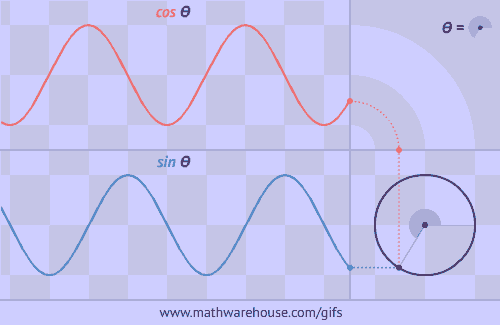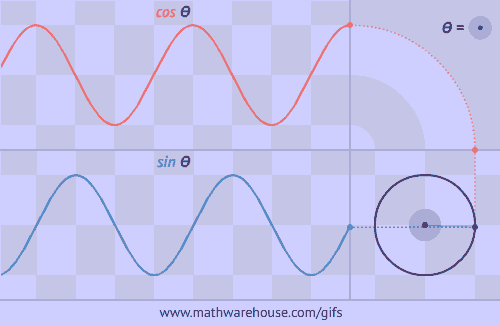
У фізиці вивчення механічних та електромагнітних коливань і хвиль тісно пов’язано з поняттям тригонометричних функцій. Адже ці коливання здійснюються за законом синуса або косинуса. Вони дають можливість глибше зрозуміти природу навколишнього світу.
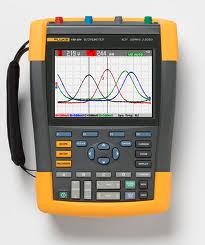
Графіком коливань математичного маятника є синусоїда.
Осцилограф.
Сьогодні у нас незвичний урок – ми навчимось будувати графіки тригонометричних функцій, а перевіряти будемо за допомогою комп’ютера.
2. Перевірка домашнього завдання, повторення раніше вивченого матеріалу.
Самоперевірка за зразком на дошці.
Оскільки ми з вами працюємо на довірі, то я пропоную після перевірки самостійно виставити оцінки собі за домашнє завдання.
3. Актуалізація суб’єктивного досвіду і опорних знань
«Подорож у дитинство»
В усіх нас постійно живе дитина, тому люди у досить зрілому віці люблять гратися. Зараз я пропоную вашій увазі гру «Угадай». Я показуватиму предмет, який можна використати для побудови певної фігури, а ви повинні назвати цю фігуру та основне рівняння, яким вона задається.
Фігури: коло, пряма, парабола,синусоїда.
4. Вивчення нового матеріалу (вступні, мотиваційні та пізнавальні вправи).
1. Евристична бесіда учителя з класом
Ми вміємо будувати графіки функцій y=sin x, y=cos x.
Також ми зможемо будувати графіки складніших функцій, наприклад:
- y=2sin(2x+ π/3)-1;
- y=|(cos|2x-π/3|)| та інші.
Побудова такого та інших графіків буде зводитися до побудови відомого,зокрема, у=sin x, y= cos x, а потім наступні кроки його перетворення.
Тому, перш за все нагадаємо, яким чином можна здійснювати побудову графіків за допомогою геометричних перетворень відомих графіків
функцій.
2. Інтерактивна вправа «Асоціативний кущ»
Вказати загальний вигляд функції, яку можна отримати за допомогою наступних перетворень:
1. Графік функції можна дістати з графіка відомої функції y=f(x) за допомогою відображення симетрії відносно осі ОХ
2. Графік функції можна дістати з графіка відомої функції y=f(x) за допомогою відображення симетрії відносно осі ОУ
3. Графік функції збігається з графіком функції y=f(x), якщо x≥0 , і з графіком y=f(-x), якщо x<0.
4. Щоб побудувати графік функції досить побудувати усі точки графіка функції y=f(x) з невід’ємними ординатами, а ту частину графіка, яка розміщена нижче осі ох, відобразити симетрично осі OX.
5. Графік функції можна дістати з графіка відомої функції y=f(x) за допомогою паралельного перенесення його вгору для “+” та вниз для ”–“ у напрямі осі ОУ.
6. Графік функції можна дістати з графіка відомої функції y=f(x) за допомогою паралельного перенесення його вліво для “+” та вправо для ”–“ у напрямі осі OX.
7. Графік функції можна дістати з графіка відомої функції y=f(x) за допомогою розтягування його в а разів від осі ох, якщо а>1, і за допомогою стиснення в а разів до осі ох, якщо 0<a<1.
8. Графік функції можна дістати з графіка відомої функції y=f(x) за допомогою стиснення його в а разів до осі ОУ, якщо а>1, і за допомогою розтягування в а разів від осі ОУ, якщо 0<a<1.
3. Коментована побудова графіків
А зараз продемонструйте практично побудову графіків функцій за допомогою геометричних перетворень відомих графіків функцій.
№ 761. Побудуйте графік функції :
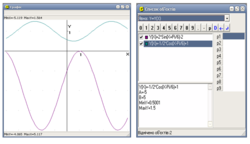
1)y=2sin(x+ π/6)-2;
Графік функції y=sin x
а) зміщуємо вліво на π/6 (на 1 клітинку);
б) розтягуємо від осі OX у 2 рази;
в) опускаємо вниз на 2 одиниці (4 клітинки).
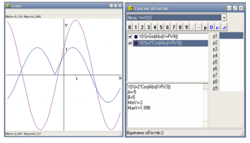
2) y= -1/2 cos(x- π/( 6 ))+1;
Графік функції y=cos x
а) зміщуємо вправо на π/6 (на 1 клітинку);
б) стискуємо до осі OX у 2 рази;
в) відображаємо симетрично відносно осі OX;
г) переміщаємо вгору на1 одиницю (2 клітинки).
4. Робота в парах.
Учні діляться на пари. Один з учнів пари займає місце за ПК, інший залишається за робочим столом. Пара отримує однакове завдання. Учень за комп'ютером будує графік за допомогою програми GRAN, інший учень – у зошиті. По закінченню виконання завдання, здійснюється взаємоперевірка.
Даний процес можна значно полегшити, якщо у своїй роботі буде використано програму GRAN. Давайте познайомимося із нею.
Щоб запустити програму на виконання:
- потрібно знайти папку GRAN, а в ній файл gran.exe,
- запустити файл на виконання.
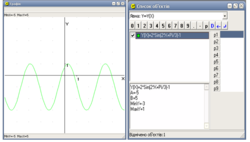
Після виконання вказаних дій на екрані побачимо вікно програми, яке складатиметься із меню, панелі інструментів, системи координат, вікна вибору, статусу та відображення функції.
Зауваження – щоб вірно ввести функцію, потрібно дотримуватися правил утворення виразів. Для прикладу розглянемо вираз та nзапишемо його у потрібній формі:
(3*sin(x)+cos((1/2)*x))/(2–4*abs(x))
№ 763.Побудуйте графік функції:
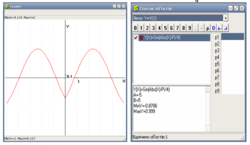
1)y=sin|x+π/4|;
2) y=2cos|x-π/3|.
№767. Побудуйте графік функції : y=sin(|x|-π/4).
5. Додаткове завдання (для учнів, що швидко справилися з роботою)
Використовуючи програму GRAN, побудувати графіки функцій та описати по кроках побудову.
№ 769. Побудуйте графік функції : y=2sin(2x+ π/3)-1.
5. Підсумки уроку.
Рефлексивна бесіда
Учні обирають ті твердження, які хотіли б продовжити
- Під час заняття я .... дізнався/дізналася ....
- Повторив/повторила ....
- Навчився/навчилася ....
- Зробив/зробила успіхи ....
- Труднощі відчував/відчувала у ....
- Мене захопило ....
- Бажаю продовжити ....
6. Повідомлення домашнього завдання.
Повторити перетворення графіків функцій.
№762. Побудуйте графік функції:
1) y=-3sin(x- π/( 3))+1/2;
2) y=2cos(x+ π/4 )-1.
№764. Побудуйте графік функції:
1) y=2sin|x+π/6|;
2) y=-cos|x-π/4| .
№768. Побудуйте графік функції: y=2cos(|x|-π/3)-1.
Методичні та дидактичні матеріали
- Блог учителя з посиланнями на матеріали до уроку Блог
- Макет для майбутньої стінгазети або постеру Газета
- Тест для перевірки знань учнів Тест
- Ментальні карти Ментальні карти
- Ігра для учнів Значення тригонометричних функцій
- Публікація або інфографіка Публікація
- Електронний журнал Журнал
- Методичні або дидактичні матеріали до уроку Перетворення синуса
Інформаційні ресурси
Друковані джерела
Відеоматеріали
Електронні ресурси
Автор статті
Студентка фізико-математичного факультету 6 курсу, спеціальність "Математика"
Центральноукраїнський державний педагогічний університет імені Володимира Винниченка