Відмінності між версіями «Стаття проекту "Урок майбутнього!" Самойленко Дарини»
2490625 (обговорення • внесок) (→Тема уроку) |
2490625 (обговорення • внесок) (→Методичні та дидактичні матеріали) |
||
| (не показано 27 проміжних версій цього учасника) | |||
| Рядок 12: | Рядок 12: | ||
=Тема уроку= | =Тема уроку= | ||
| − | '''Конус''' | + | <big>'''Конус'''</big> |
===Тип уроку=== | ===Тип уроку=== | ||
''Вибрати один із списку: | ''Вибрати один із списку: | ||
| Рядок 25: | Рядок 25: | ||
=Хід уроку= | =Хід уроку= | ||
| − | ===1. | + | ===1. Організаційна частина=== |
| − | + | Привітання. Перевірка стану готовності учнів до уроку. | |
| − | [ | + | [https://urokkonus.blogspot.com/ Посилання на блог учителя з навчально-методичними матеріалами до уроку] |
| − | ===2. | + | ===2. Повторення матеріалу з теми "Циліндр"=== |
| − | + | Проводиться тест з теми "Циліндр" | |
| − | ===3. | + | ===3. Сприйняття нового матеріалу=== |
| + | [[Файл:124.png|праворуч|100пкс]] | ||
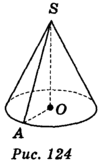
| + | <big>Прямим круговим конусом називається тіло, утворене обертанням плоского прямокутного трикутника навколо одного із його катетів (рис. 124). | ||
| + | Якщо прямокутний трикутник SАО обертається навколо катета SO, то його гіпотенуза описує бічну поверхню, а катет ОА — круг — основу конуса. Радіус цього круга називається радіусом конуса; точка S, відрізок SА, відрізок SO, пряма SO називаються відповідно вершиною, твірною, висотою і віссю конуса.<br /> | ||
| + | [[Файл:125(1).png|праворуч|100пкс]] | ||
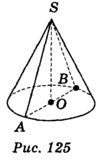
| + | Осьовий переріз конуса — переріз конуса площиною, яка проходить через його вісь. Всі осьові перерізи конуса являють собою рівнобедрені трикутники, рівні між собою. На рис. 125 ∆SАВ — осьовий переріз (SА = SВ). Висотою конуса називається перпендикуляр, опущений з його вершини на площину основи. У прямого кругового конуса основа висоти збігається з центром основи. На рис. 125 S0 — висота конуса. | ||
| + | Площа бічної поверхні конуса дорівнює добутку половини довжини кола основи на твірну: Sбічн = πRl.<br /> | ||
| + | Площею повної поверхні конуса називається сума площ бічної поверхні та основи. Для обчислення площі повної поверхні конуса Sкон одержуємо: | ||
| + | Sкон = Sбічн + Sосн, Sкон = πRl + πR^2 = πR(l + R).<br /> | ||
| + | Об'єм конуса дорівнює третині добутку площі його основи на висоту: | ||
| + | V = πR^2H.</big> | ||
| − | ===4. | + | ===4. Застосування здобутих знань до розв'язування задач=== |
| + | <big> | ||
| + | 1. Наведіть приклади побутових предметів, які мають форму конуса. <br /> | ||
| + | 2. Радіус основи конуса дорівнює 6 см, висота — 8 см. Знайдіть твір¬ну конуса. <br /> | ||
| + | 3. Твірна конуса дорівнює l і нахилена до площини основи під кутом α. Знайдіть:<br /> | ||
| + | а) висоту конуса;<br /> | ||
| + | б) радіус основи конуса;<br /> | ||
| + | в) площу основи;<br /> | ||
| + | г) площу осьового перерізу;<br /> | ||
| + | д) відстань від центра основи конуса до твірної.<br /> | ||
| + | 4. Радіус основи конуса дорівнює 28 см, а твірна довша висоти на 8 см. Знайдіть площу осьового перерізу конуса. <br /> | ||
| + | 5. Відношення площі основи конуса до площі осьового перерізу дорівнює π. Знайдіть кут нахилу твірної до основи.<br /> | ||
| + | 6. Висота конуса дорівнює 6 см, радіус основи — 8 см. Знайдіть бічну поверхню конуса.<br /> | ||
| + | 7. Твірна конуса дорівнює 5 см, висота — 4 см. Знайдіть площу повної поверхні конуса.<br /> | ||
| + | 8. Осьовий переріз конуса — правильний трикутник, сторона якого дорівнює 6 см. Знайдіть бічну поверхню конуса.<br /> | ||
| + | 9. Висота конуса дорівнює 6 см, твірна — 10 см. Знайдіть об'єм конуса.<br /> | ||
| + | 10. Осьовий переріз конуса — прямокутний трикутник із гіпотенузою 12 см. Знайдіть об'єм конуса.</big> | ||
| − | + | ===5. Підсумки уроку.=== | |
| + | <big>Учні розв'язують кросворд з теми "Конус"</big> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
===6. Повідомлення домашнього завдання.=== | ===6. Повідомлення домашнього завдання.=== | ||
| − | ... | + | # Вивчити формули площі поверхні та об'єму конуса. |
| − | + | # Розв'язати задачу: Твірна і висота конуса дорівнюють 15 см і 9 см. Знайдіть площу його поверхні та об'єм. | |
=Методичні та дидактичні матеріали= | =Методичні та дидактичні матеріали= | ||
| − | # | + | #[https://urokkonus.blogspot.com/ Блог учителя з посиланнями на матеріали до уроку] |
| − | # | + | #[http://wikiwall.ru/wall/551e8c5515d72b1d02c539ad16182a70 Макет для майбутньої стінгазети або постеру] |
| − | + | #[https://docs.google.com/forms/d/e/1FAIpQLSdefqioC7_zPQBxRWPFDdUAuHHh369qrIIX3HYtlxARBPf7Dw/viewform?usp=sf_link Тест для перевірки знань учнів] | |
| − | #Ментальні карти | + | #[https://coggle.it/diagram/WwVRaufgIxOtoXlI/t/-/ffdf433334e15582a6e1853da61321aa9726b7f192ab21ab6d66e460211a76b5 Ментальні карти] |
| − | # | + | #[https://learningapps.org/display?v=p1iij9bqt18 Кросворд з теми "Конус"] |
| − | # | + | #[https://learningapps.org/watch?v=p68zr9ihn18 Відеоматеріал] |
| − | # | + | #[[Плакат виготовлений у Canva]] |
| − | # | + | #[https://docs.google.com/spreadsheets/d/1uUT5u483z-KWkuato5Bqt9NmIYls2B5icE6Za-wf01E/edit?usp=sharing Електронний журнал] |
| − | + | ||
| − | + | ||
| − | + | ||
=Інформаційні ресурси= | =Інформаційні ресурси= | ||
| − | |||
| − | |||
| − | |||
| − | |||
===Відеоматеріали=== | ===Відеоматеріали=== | ||
| − | #... | + | #[https://www.youtube.com/watch?v=kXOYcy4ZAS0&t=1s Конус. Відео-урок] |
| − | #.. | + | #[https://www.youtube.com/watch?v=jbi1II6FPc8 Як виготовити конус власноруч] |
| − | #.. | + | #[https://www.youtube.com/watch?v=wyCglJE8II4 Цилиндр, конус, шар] |
| − | + | #[https://www.youtube.com/watch?v=jicXmYnEhNE Усеченный конус из бумаги. Как сделать усеченный конус.] | |
| − | + | #[https://www.youtube.com/watch?v=SSsuZWf55IA Переріз конуса площиною] | |
| − | #... | + | |
| − | + | ||
| − | #.. | + | |
---- | ---- | ||
==Автор статті== | ==Автор статті== | ||
| − | + | Студентка фізико-математичного факультету. 6 курсу, спеціальність "Математика-Інформатика" | |
| − | + | ||
| − | + | ||
| − | [[ | + | [[Користувач:2490625|Самойленко Дарина]] |
[http://kspu.kr.ua/ Центральноукраїнський державний педагогічний університет імені Володимира Винниченка] | [http://kspu.kr.ua/ Центральноукраїнський державний педагогічний університет імені Володимира Винниченка] | ||
Поточна версія на 13:20, 31 травня 2018
Зміст
Навчальний предмет
Геометрія
Вік учнів, клас
16-18 років, 11 клас
Тема уроку
Конус
Тип уроку
Вибрати один із списку: Урок засвоєння нових знань
Мета уроку
Навчальна мета систематизувати та узагальнити знання та вміння учнів з теми «Циліндр»; вивчити конус та його елементи; застосувати математичні знання під час розв’язання задач та використовувати у своїй професії.
Розвивальна мета розвивати просторову уяву, логічне мислення, вміння висловлювати та обґрунтовувати свою думку, формувати вміння вирішувати проблемні ситуації, бажання пізнавати нове, прививати інтерес до математики.
Виховна мета сприяти вихованню відповідальності учнів за результати виконання завдань, сприяти розвитку комунікативних умінь, взаємоповаги, взаємодопомоги, почуття колективізму, культуру поведінки.
Хід уроку
1. Організаційна частина
Привітання. Перевірка стану готовності учнів до уроку.
Посилання на блог учителя з навчально-методичними матеріалами до уроку
2. Повторення матеріалу з теми "Циліндр"
Проводиться тест з теми "Циліндр"
3. Сприйняття нового матеріалу
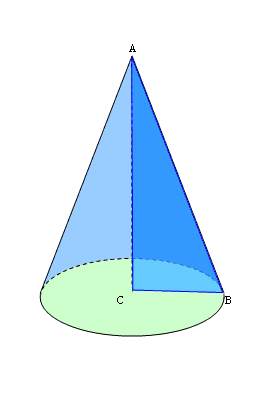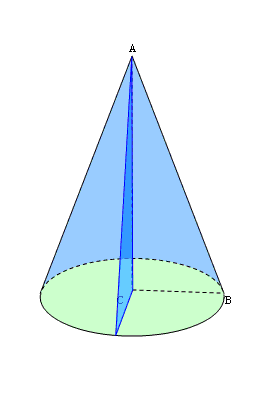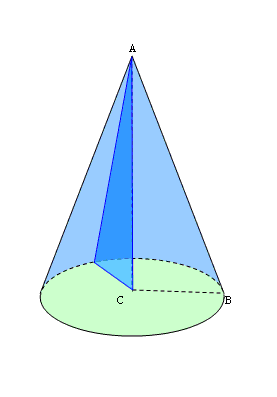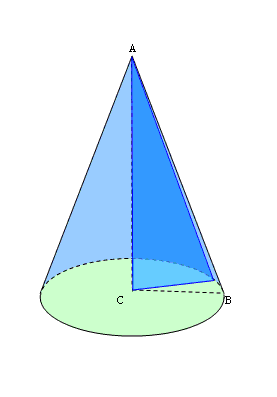
Прямим круговим конусом називається тіло, утворене обертанням плоского прямокутного трикутника навколо одного із його катетів (рис. 124).
Якщо прямокутний трикутник SАО обертається навколо катета SO, то його гіпотенуза описує бічну поверхню, а катет ОА — круг — основу конуса. Радіус цього круга називається радіусом конуса; точка S, відрізок SА, відрізок SO, пряма SO називаються відповідно вершиною, твірною, висотою і віссю конуса.
Осьовий переріз конуса — переріз конуса площиною, яка проходить через його вісь. Всі осьові перерізи конуса являють собою рівнобедрені трикутники, рівні між собою. На рис. 125 ∆SАВ — осьовий переріз (SА = SВ). Висотою конуса називається перпендикуляр, опущений з його вершини на площину основи. У прямого кругового конуса основа висоти збігається з центром основи. На рис. 125 S0 — висота конуса.
Площа бічної поверхні конуса дорівнює добутку половини довжини кола основи на твірну: Sбічн = πRl.
Площею повної поверхні конуса називається сума площ бічної поверхні та основи. Для обчислення площі повної поверхні конуса Sкон одержуємо:
Sкон = Sбічн + Sосн, Sкон = πRl + πR^2 = πR(l + R).
Об'єм конуса дорівнює третині добутку площі його основи на висоту:
V = πR^2H.
4. Застосування здобутих знань до розв'язування задач
1. Наведіть приклади побутових предметів, які мають форму конуса.
2. Радіус основи конуса дорівнює 6 см, висота — 8 см. Знайдіть твір¬ну конуса.
3. Твірна конуса дорівнює l і нахилена до площини основи під кутом α. Знайдіть:
а) висоту конуса;
б) радіус основи конуса;
в) площу основи;
г) площу осьового перерізу;
д) відстань від центра основи конуса до твірної.
4. Радіус основи конуса дорівнює 28 см, а твірна довша висоти на 8 см. Знайдіть площу осьового перерізу конуса.
5. Відношення площі основи конуса до площі осьового перерізу дорівнює π. Знайдіть кут нахилу твірної до основи.
6. Висота конуса дорівнює 6 см, радіус основи — 8 см. Знайдіть бічну поверхню конуса.
7. Твірна конуса дорівнює 5 см, висота — 4 см. Знайдіть площу повної поверхні конуса.
8. Осьовий переріз конуса — правильний трикутник, сторона якого дорівнює 6 см. Знайдіть бічну поверхню конуса.
9. Висота конуса дорівнює 6 см, твірна — 10 см. Знайдіть об'єм конуса.
10. Осьовий переріз конуса — прямокутний трикутник із гіпотенузою 12 см. Знайдіть об'єм конуса.
5. Підсумки уроку.
Учні розв'язують кросворд з теми "Конус"
6. Повідомлення домашнього завдання.
- Вивчити формули площі поверхні та об'єму конуса.
- Розв'язати задачу: Твірна і висота конуса дорівнюють 15 см і 9 см. Знайдіть площу його поверхні та об'єм.
Методичні та дидактичні матеріали
- Блог учителя з посиланнями на матеріали до уроку
- Макет для майбутньої стінгазети або постеру
- Тест для перевірки знань учнів
- Ментальні карти
- Кросворд з теми "Конус"
- Відеоматеріал
- Плакат виготовлений у Canva
- Електронний журнал
Інформаційні ресурси
Відеоматеріали
- Конус. Відео-урок
- Як виготовити конус власноруч
- Цилиндр, конус, шар
- Усеченный конус из бумаги. Как сделать усеченный конус.
- Переріз конуса площиною
Автор статті
Студентка фізико-математичного факультету. 6 курсу, спеціальність "Математика-Інформатика"
Центральноукраїнський державний педагогічний університет імені Володимира Винниченка