Поточна версія на 19:10, 28 травня 2018

Зміст

1 Навчальний предмет
- 1.1 Вік учнів, клас
2 Тема уроку
- 2.1 Тип уроку
- 2.2 Мета уроку
3 Хід уроку
4 Методичні та дидактичні матеріали
5 Інформаційні ресурси

Навчальний предмет

Геометрія

Вік учнів, клас

16-17 років, 11 клас

Тема уроку

ПЕРЕТВОРЕННЯ СИМЕТРІЇ У ПРОСТОРІ

Тип уроку

Урок засвоєння нових знань;

Мета уроку

Навчальна мета: сформувати в учнів знання про перетворення симетрії у просторі, вміння застосовувати отримані знання під час розв’язування задач;
Розвивальна мета: розвивати просторові уявлення, пам’ять, логічне мислення;
Виховна мета: виховувати наполегливість, працьовитість.

Хід уроку

1. ОРГАНІЗАЦІЙНИЙ ЕТАП

Привітання з учнями. Перевірка готовності учнів до уроку. Налаштування на роботу.

Блог учителя "Цікава шкільна геометрія"

2. ПЕРЕВІРКА ДОМАШНЬОГО ЗАВДАННЯ

На дошці записано кілька «домашніх задач» з навмисно допущеними помилками. Учням необхідно віднайти та виправити ці помилки.

3. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ

Фронтальна бесіда:

Назвіть види перетворень фігур на площині.
Назвіть види перетворень симетрії на площині.
Які дві точки називають симетричними відносно даної точки на площині? відносно прямої на площині?
Назвіть фігури, які мають центр симетрії.
Які відомі вам фігури на площині мають вісь симетрії?
Які властивості має перетворення симетрії на площині?

4. ФОРМУЛЮВАННЯ ТЕМИ, МЕТИ Й ЗАВДАНЬ УРОКУ; МОТИВАЦІЯ НАВЧАЛЬНОЇ ДІЯЛЬНОСТІ

Чи часто ви дивитесь у дзеркало? А чи знаєте ви, що й під час розглядання свого відображення у дзеркалі маєте справу з математикою, а саме з одним із видів просторової симетрії. Сьогодні ми поговоримо про це.

5. СПРИЙНЯТТЯ та УСВІДОМЛЕННЯ НОВОГО МАТЕРІАЛУ

Поняття симетрії відносно точки у просторі.

Точки A і A' називають симетричними відносно точки O, якщо точка O — середина відрізка AA'. Перетворенням симетрії відносно точки O (центральною симетрією) називають таке перетворення, при якому кожна точка даної фігури

переходить у точку, симетричну їй відносно точки O.

Якщо симетрія відносно точки O переводить дану фігуру в ту саму фігуру, то таку фігуру називають центральносиметричною, а точку O — її центром симетрії. Прикладом такої фігури є прямокутний паралелепіпед. Його центр симетрії — точка перетину діагоналей паралелепіпеда.

Поняття симетрії відносно прямої у просторі.

Точки A і A' називають симетричними відносно прямої l, якщо ця пряма перпендикулярна до відрізка AA' і проходить через його середину.

Перетворенням симетрії відносно прямої (осьовою симетрією) нназивають таке перетворення, при якому кожна точка фігури переходить у точку, симетричну їй відносно даної прямої. Наприклад, куб має вісь симетрії, причому не одну.

Поняття симетрії відносно площини у просторі.

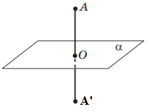
Точки A і A' називають симетричними відносно площини α, якщо ця площина перпендикулярна до відрізка AA' і проходить через його середину (рис. 1). Точки площини α вважаються симетричними самі до себе. При цьому площину α називають площиною симетрії.
Перетворенням симетрії відносно площини α називають таке перетворення, при якому кожна точка даної фігури переходить у точку, симетричну їй відносно площини α.
Якщо перетворення симетрії відносно площини α переводитьдану фігуру в себе, то таку фігуру називають симетричною відносно площини α. Наприклад, куля є симетричною відносно будь-якої площини, яка проходить через її центр.
Учитель пропонує учням ознайомитися з таблицею, заздалегідь підготовленою на дошці, і сформувати уявлення про те, що точки, симетричні точці A(x;y;z) відносно початку координат,координатних осей і площин, мають такі координати.

6. ОСМИСЛЕННЯ НОВОГО МАТЕРІАЛУ

Розв'язання задач:

ЗАДАЧА 1. Точки A і B симетричні відносно точки C. Знайдіть координати точки C, якщо A(5;-3;4) і B(-3;1;-2).

Відповідь: C(1;-1;1).

ЗАДАЧА 2. Точку M (a;b;c) послідовно симетрично відобразили відносно координатних площин Oxy, Oxz, Oyz. Доведіть, що отримана при цьому точка M' симетрична точці M відносно початку координат.

Доведення: Точка M (a;b;c) при симетрії відносно площини Oxy переходить у точку N (a;b;-c). Точка N (a;b;-c) − при симетрії відносно площини Oxz переходить у точку K (a;-b;-c).Точка K (a;-b;-c) при симетрії відносно площини Oyz переходить у точку M' (-a;-b;-c). Середина відрізка MM' має координати (0;0;0). Отже, початок координат — центр симетрії точок M і M'.

ЗАДАЧА 3. Точка A(5;2;3) належить колу із центром O. Знайдіть радіус кола, якщо при симетрії відносно осі ординат центр кола переходить у точку O(-2;1;1).

Розв’язання: Оскільки точка O при симетрії відносно осі ординат перейшла в точку O′(−2;1;1),то точка O має координати: O(2;1;−1).
Неможливо розібрати вираз (невідома помилка): R^2=OA^2=(5-2)^2+(2-1)^2+(3+1)^2=9+1+16;

Неможливо розібрати вираз (невідома помилка): R=\sqrt{26}

Відповідь:Неможливо розібрати вираз (невідома помилка): R=\sqrt{26} .

ЗАДАЧА 4. Дано точки Неможливо розібрати вираз (невідома помилка): A(0;-4;5)

і Неможливо розібрати вираз (невідома помилка): B(6;8;-1).
Знайдіть координати точки, симетричної середині відрізка AB відносно: а) точки Неможливо розібрати вираз (невідома помилка): O(0;-2;2)

б) осі аплікат; в) площини Oxy.

Розв’язання: а) Знайдемо середину відрізка AB — точку Неможливо розібрати вираз (невідома помилка): C(x_{1};y_{1};z_{1}).

Неможливо розібрати вираз (невідома помилка): x_{1}=\frac{0+6}{2}=3;
Неможливо розібрати вираз (невідома помилка): y_{1}=\frac{-4+8}{2}=2;
Неможливо розібрати вираз (невідома помилка): z_{1}=\frac{5-1}{2}=2.
Неможливо розібрати вираз (невідома помилка): C(3;2;2).
Оскільки точка Неможливо розібрати вираз (невідома помилка): C_{1}(x_{2};y_{2};z_{2})
симетрична точці С відносно точки O(0;-2;2), то точка O — середина відрізка Неможливо розібрати вираз (невідома помилка): CC_{1}

. Тоді Неможливо розібрати вираз (невідома помилка): \frac{x_{2}+3}{2}=0;

Неможливо розібрати вираз (невідома помилка): x_{2}=-3
 і точка C' має координати: Неможливо розібрати вираз (невідома помилка): \frac{y_{2}+2}{2}=-2;
Неможливо розібрати вираз (невідома помилка): y_{2}=-6;
Неможливо розібрати вираз (невідома помилка): \frac{z_{2}+2}{2}=2;
Неможливо розібрати вираз (невідома помилка): z_{2}=2.
. Отже, Неможливо розібрати вираз (невідома помилка): C_{1}(-3;-6;2).

б) Оскільки точка Неможливо розібрати вираз (невідома помилка): C_{2}

симетрична точці С відносно осі аплікат, то точка Неможливо розібрати вираз (невідома помилка): C_{2}

, яка їй симетрична, має координати: Неможливо розібрати вираз (невідома помилка): C_{2}(-3;-2;2).
в) Точка Неможливо розібрати вираз (невідома помилка): C_{3},

симетрична точці C відносно площини Oxy, має координати: Неможливо розібрати вираз (невідома помилка): C_{3}(3;2;-2).

Відповідь: Неможливо розібрати вираз (невідома помилка): C_{1}(-3;-6;2),

Неможливо розібрати вираз (невідома помилка): C_{2}(-3;-2;2),
Неможливо розібрати вираз (невідома помилка): C_{2}(-3;-2;2).

ЗАДАЧА 5. Доведіть, що якщо дві прямі симетричні відносно площини α, то вони лежать в одній площині.

Доведення: Розглянемо довільні точки A і B прямої a, які при симетрії відносно площини α переходять у точки A' і B' прямої a'. За означенням симетрії відносно площини AA'⊥α, BB'⊥α, отже, AA'||BB' . Очевидно, що точки A, A', B, B' лежать у площині, яка визначається цими паралельними прямими, тобто прямі a і a' також лежать у цій площині.

7. ПІДБИТТЯ ПІДСУМКІВ УРОКУ

Фронтальна бесіда

Що називають перетворенням симетрії відносно точки? відносно прямої? відносно площини?
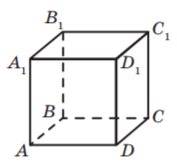
У кубі ABCDA1B1C1D1 (рис. 2) діагоналі основи ABCD перетинаються в точці O. Визначте:

точку, симетричну точці A відносно площини BDD1;
пряму, симетричну прямій CD відносно точки O;
площину, симетричну площині AA1B1 відносно точки O;
пряму, симетричну прямій DD1 відносно площини AA1C1;
площину, симетричну площині AA1B1 відносно прямої BB1.

8. ДОМАШНЄ ЗАВДАННЯ

Вивчити конспект;
№335; №351; №395; (підручник "Бевз В.Г. Геометрія. Профільний рівень" 2011р)
Накреслити куб ABCDA'B'C'D'. Побудувати фігуру, в яку переходить цей куб при симетрії відносно: а) середини ребра A'B'; б) прямої BD.

Методичні та дидактичні матеріали

Інформаційні ресурси

Друковані джерела

Александров А.Д. "Стереометрия. Геометрия в пространстве"
Шарль П'єр Франсуа Дюпен "Геометрія мистецтв і ремесел"
Герман Вейль "Симметрия"

Відеоматеріали

Електронні ресурси

Автор статті

Студентка фізико-математичного факультету, групи МІ17М, спеціальність математика

Гелевер Ірина

Центральноукраїнський державний педагогічний університет імені Володимира Винниченка

@@ Рядок 47: / Рядок 47: @@
 Точки A і A' називають ''симетричними відносно точки O'', якщо точка O — середина відрізка AA'.
 ''Перетворенням симетрії відносно точки O'' (центральною симетрією) називають таке перетворення, при якому кожна точка даної фігури
-переходить у точку, симетричну їй відносно точки O.<br>
+переходить у точку, симетричну їй відносно точки O.<br>[[Файл:Площ.png|right|150px|рис. 1]]<br>
 Якщо симетрія відносно точки O переводить дану фігуру в ту саму фігуру, то таку фігуру називають ''центральносиметричною'', а точку O — її ''центром симетрії''. Прикладом такої фігури є прямокутний паралелепіпед. Його центр симетрії — точка перетину діагоналей паралелепіпеда.<br>
-#''Поняття симетрії відносно прямої у просторі.''[[Файл:Рисун1.png|right|150px]]<br>
+#''Поняття симетрії відносно прямої у просторі.''
 Точки A і A' називають ''симетричними відносно прямої l'', якщо ця пряма перпендикулярна до відрізка AA' і проходить через його середину.<br>
-''Перетворенням симетрії відносно прямої'' (осьовою симетрією) нназивають таке перетворення, при якому кожна точка фігури переходить у точку, симетричну їй відносно даної прямої. Наприклад, куб має вісь симетрії, причому не одну.<br>
+''Перетворенням симетрії відносно прямої'' (осьовою симетрією) нназивають таке перетворення, при якому кожна точка фігури переходить у точку, симетричну їй відносно даної прямої. Наприклад, куб має вісь симетрії, причому не одну.<br>[[Файл:Tabb.png|right|400px]]
-# ''Поняття симетрії відносно площини у просторі.''[[Файл:Tabb.png|right|400px]]<br>
+# ''Поняття симетрії відносно площини у просторі.''<br>
 Точки A і A' називають ''симетричними відносно площини α'', якщо ця площина перпендикулярна до відрізка AA' і проходить
 через його середину (рис. 1). Точки площини α вважаються симетричними самі до себе. При цьому площину α називають ''площиною симетрії.''<br>
@@ Рядок 64: / Рядок 64: @@
 ===6.  ОСМИСЛЕННЯ НОВОГО МАТЕРІАЛУ===
 Розв'язання задач: <br>
-*1. Точки A і B симетричні відносно точки C. Знайдіть координати точки C, якщо A(5;-3;4) і B(-3;1;-2).
+*<b>ЗАДАЧА 1.</b> Точки A і B симетричні відносно точки C. Знайдіть координати точки C, якщо A(5;-3;4) і B(-3;1;-2).
-(Відповідь: C(1;-1;1)).
+''Відповідь:'' C(1;-1;1).
-*2. Точку M (a;b;c) послідовно симетрично відобразили відносно координатних площин Oxy, Oxz, Oyz. Доведіть, що отримана при цьому точка M' симетрична точці M відносно початку координат.
+*<b>ЗАДАЧА 2.</b> Точку M (a;b;c) послідовно симетрично відобразили відносно координатних площин Oxy, Oxz, Oyz. Доведіть, що отримана при цьому точка M' симетрична точці M відносно початку координат.
 ''Доведення:'' Точка M (a;b;c) при симетрії відносно площини Oxy переходить у точку N (a;b;-c). Точка N (a;b;-c) − при симетрії відносно площини Oxz переходить у точку K (a;-b;-c).Точка K (a;-b;-c) при симетрії відносно площини Oyz переходить у точку M' (-a;-b;-c). Середина відрізка MM' має координати (0;0;0). Отже, початок координат — центр симетрії точок M і M'.
-*3.Точка A(5;2;3) належить колу із центром O. Знайдіть радіус кола, якщо при симетрії відносно осі ординат центр кола переходить у точку O′(−2;1;1).
+*<b>ЗАДАЧА 3.</b> Точка A(5;2;3) належить колу із центром O. Знайдіть радіус кола, якщо при симетрії відносно осі ординат центр кола переходить у точку O(-2;1;1).
-''Розв’язання:'' Оскільки точка O при симетрії відносно осі ординат перейшла в точку O′(−2;1;1), то точка O має координати:
+''Розв’язання:'' Оскільки точка O при симетрії відносно осі ординат перейшла в точку  O′(−2;1;1),то точка O має координати: O(2;1;−1). <br>
-O(2;1;−1). <br>
 <math>R^2=OA^2=(5-2)^2+(2-1)^2+(3+1)^2=9+1+16;</math> <math>R=\sqrt{26}</math><br>
-(Відповідь:<math>R=\sqrt{26}</math>).
+''Відповідь:''<math>R=\sqrt{26}</math>.
-*4.Дано точки A(0'-4;5) і B(6;8;−1). Знайдіть координати точки, симетричної середині відрізка AB відносно: а) точки O(0;-2;2); б) осі аплікат; в) площини Oxy.
+*<b>ЗАДАЧА 4.</b> Дано точки <math>A(0;-4;5)</math> і <math>B(6;8;-1).</math> Знайдіть координати точки, симетричної середині відрізка AB відносно: а) точки <math>O(0;-2;2)</math>; б) осі аплікат; в) площини Oxy.
-''Розв’язання:'' а) Знайдемо середину відрізка AB — точку <math>C(x_{1};y_{1};z_{1}).</math> <br>
+''Розв’язання:'' а) Знайдемо середину відрізка AB — точку <math>C(x_{1};y_{1};z_{1}).</math> <math>x_{1}=\frac{0+6}{2}=3;</math> <math>y_{1}=\frac{-4+8}{2}=2;</math> <math>z_{1}=\frac{5-1}{2}=2.</math> <math>C(3;2;2).</math> Оскільки точка <math>C_{1}(x_{2};y_{2};z_{2})</math> симетрична точці С відносно точки O(0;-2;2), то точка O — середина відрізка <math>CC_{1}</math>. Тоді
-<math>x_{1}=\frac{0+6}{2}=3;</math> <math>y_{1}=\frac{-4+8}{2}=2;</math> <math>z_{1}=\frac{5-1}{2}=2.</math>
+<math>\frac{x_{2}+3}{2}=0;</math> <math>x_{2}=-3</math>  і точка C' має координати: <math>\frac{y_{2}+2}{2}=-2;</math> <math>y_{2}=-6;</math> <math>\frac{z_{2}+2}{2}=2;</math> <math>z_{2}=2.</math> . Отже, <math>C_{1}(-3;-6;2).</math><br>
-C(3;2;2). Оскільки точка <math>C(x_{2};y_{2};z_{2})</math> симетрична точці С відносно точки O(0;-2;2), то точка O — середина відрізка CC'. Тоді
+б) Оскільки точка <math>C_{2}</math> симетрична точці С відносно осі аплікат, то точка <math>C_{2}</math>, яка їй симетрична, має координати: <math>C_{2}(-3;-2;2).</math><br>
-<math>\frac{x_{2}+3}{2}=0;</math> <math>x_{2}=-3</math>  і точка C' має координати: <math>\frac{y_{2}+2}{2}=-2;</math> <math>y_{2}=-6</math> <math>\frac{z_{2}+2}{2}=2;</math> <math>z_{2}=2.</math>
+в) Точка <math>C_{3},</math> симетрична точці C відносно площини Oxy, має координати: <math>C_{3}(3;2;-2).</math><br>
+''Відповідь:'' <math>C_{1}(-3;-6;2),</math> <math>C_{2}(-3;-2;2),</math> <math>C_{2}(-3;-2;2).</math>
+*<b>ЗАДАЧА 5.</b> Доведіть, що якщо дві прямі симетричні відносно площини α, то вони лежать в одній площині.
+''Доведення:'' Розглянемо довільні точки A і B прямої a, які при симетрії відносно площини α переходять у точки A' і B' прямої a'. За означенням симетрії відносно площини AA'⊥α, BB'⊥α, отже, AA'||BB' . Очевидно, що точки A, A', B, B' лежать у площині, яка визначається цими паралельними прямими, тобто прямі a і a' також лежать у цій площині.
 ===7. ПІДБИТТЯ ПІДСУМКІВ УРОКУ===
+Фронтальна бесіда[[Файл:Куб.png|right|рис. 2]]
+# Що називають перетворенням симетрії відносно точки? відносно прямої? відносно площини?
+# У кубі ABCDA1B1C1D1 (рис. 2) діагоналі основи ABCD перетинаються в точці O. Визначте:
+*точку, симетричну точці A відносно площини BDD1;
+*пряму, симетричну прямій CD відносно точки O;
+*площину, симетричну площині AA1B1 відносно точки O;
+*пряму, симетричну прямій DD1 відносно площини AA1C1;
+*площину, симетричну площині AA1B1 відносно прямої BB1.
+===8. ДОМАШНЄ ЗАВДАННЯ===
+*Вивчити конспект;
+*№335; №351; №395; (підручник "Бевз В.Г. Геометрія. Профільний рівень" 2011р)
+*Накреслити куб ABCDA'B'C'D'. Побудувати фігуру, в яку переходить цей куб при симетрії відносно: а) середини ребра A'B'; б) прямої BD.
 =Методичні та дидактичні матеріали=
-#Блог учителя з посиланнями на матеріали до уроку [https://schgeometry.blogspot.com/ "Цікава шкільна геометрія"]
+#[https://schgeometry.blogspot.com/ Блог "Цікава шкільна геометрія"]
 #[[Стінгазета "КАЛЕЙДОСКОП"]]
 #[[Буклет "Головоломки на складання симетричних фігур"]]
-#Ментальні карти (Coogle, MindMeister, Minmodo тощо)
+# [https://www.mindmeister.com/1098340998#/ Ментальна карта]
-#Тест для перевірки знань учнів (до 10 тестових завдань) (Google Форми)
+#[http://master-test.net/ru/quiz/testing/id/114980/ Тест]
 #Ігри для учнів: [https://www.studystack.com/crossword-2778103 Кросворд], [https://www.jigsawplanet.com/?rc=play&pid=26a729fb96d0 Пазл]
 #[https://docs.google.com/spreadsheets/d/1lYRZkxOZcyKTIrJ0Sf6ZxmE_d9Y-FfDu00Zwcjpewfo/template/preview?usp=drive_web&ouid=%7BuserId%7D Електронний журнал]
-#Методичні або дидактичні матеріали до уроку, що зроблені у ППЗ із фаху (словники, стрічка часу, обчислювальні програми, геосервіси тощо)
 =Інформаційні ресурси=
@@ Рядок 98: / Рядок 112: @@
 ===Відеоматеріали===
-#...
+#[https://youtu.be/d7u7D3N6HpI/ Симетрія у просторі]
-#...
+#[https://youtu.be/MErYun1EyY0/ Симетрія привильних багатогранників]
-#...
 ===Електронні ресурси===

Відмінності між версіями «Стаття проекту "Урок майбутнього!" Гелевер Ірина»