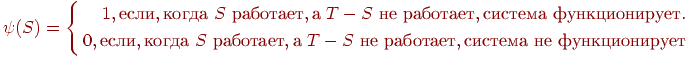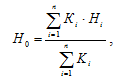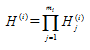Відмінності між версіями «Надійність комп'ютерних мереж»
4565426 (обговорення • внесок) м |
|||
| (не показано 22 проміжні версії 5 учасників) | |||
| Рядок 1: | Рядок 1: | ||
| − | == | + | == Основні визначення == |
| − | + | Забезпечення надійності комп’ютерних систем здійснюється в двох напрямах. В першому випадку забезпечення надійності комп’ютерних систем визначається відсутністю відмов, збоїв, помилок та несправностей. В другому - можливістю швидкого відновлення апаратури та обчислювального процесу. | |
| − | + | '''Надійність''' можна визначити як властивість об’єкта зберігати в часі у визначених межах значення всіх параметрів, іцо характеризують спроможність виконувати потрібні функції в заданих режимах і умовах застосування, технічного обслуговування, ремонтів, зберігання та транспортування. Надійність сама по собі - складна властивість, яка в залежності від призначення об’єкта та умов його експлуатації складається із сполучень властивостей: безвідмовності, довговічності, ремонтопридатності та збережності. | |
| − | + | '''Безвідмовність''' - це властивість об'єкта безперервно зберігати працездатний стан в проміжку деякого часу або деякого напрацювання. | |
| − | + | '''Напрацювання''' - це об’єм (час) роботи об'єкта. Може визначатися в іншій формі, наприклад, кількості вирішених задач або циклів роботи. | |
| − | + | '''Відмова''' - подія, яка являє собою порушення працездатності об'єкта. Вона в основному викликається фізичним руйнуванням елементів або поступовим погіршенням їх характеристик. | |
| − | + | '''Збій''' - короткочасне порушення правильної роботи обчислювального пристрою або його елемента, після якого його працездатність самовідновлюється або відновлюється оператором без проведення ремонту. Збої можуть бути викликані внутрішніми або зовнішніми перешкодами. | |
| − | + | ||
| − | + | ||
| − | + | '''Відновлення комп'ютерних систем''' — це приведення апаратури в працездатний стан шляхом заміни окремих елементів, які відмовили. Основні якості обчислювальної техніки, пов’язані з її надійністю, описуються розподіленням відмов в часі, процесами відновлення та організацією обслуговування. Покращання надійності потребує додаткових витрат на розробку, виготовлення та експлуатацію систем. При встановленні вимог до надійності обчислювальної техніки необхідно зважати на витрати, пов'язані з її розробкою та виготовленням, витрати на персонал, зайнятий ремонтом і обслуговуванням, виграти, які визначаються наслідками відмов та простоїв, зниженням ефективності або продуктивності системи, а також витрати, пов’язані із збільшенням маси або габаритів системи та ін. Якщо відмова комп’ютерних систем може спричинити собою небезпеку для життя людей або аварію, то рівень надійності визначається з такої вимоги, щоб ймовірність відмови відповідала практично неможливій події. | |
| − | + | === Методи забезпечення надійності на етапах життєвого циклу комп'ютерних систем === | |
| − | + | * Етап складання технічного завдання | |
| − | + | На даному етапі збирають всі дані, які є, про аналогічні та близькі системи, дані про умови застосування комп’ютерних систем і вимоги, що висуваються до функцій, які виконуються розглянутою системою. За сукупністю цих даних і вимог розробляються основні вимоги до надійності нової системи. | |
| − | + | * Етап ескізного проектування | |
| + | На цьому етапі обирається елементна база і визначаються особливості структури, архітектури та організації системи, яка розробляється. За цими даними проводиться попередній розрахунок надійності, виявляються найменш надійні підсистеми, і на цій основі приймається рішення про резервування системи, а також рішення про засоби та організацію технічного обслуговування, тобто профілактичні та ремонтні роботи. | ||
| + | Досліджується питання про доцільність резервування і методи автоматичного відновлення та підвищення відмовостійкості системи. | ||
| − | + | * Етап технічного і робочого проектування | |
| − | + | Під час виконання даного етапу перевіряються та уточнюються раніше прийняті рішення. Для цього використовують уточнені дані про надійність, отримані на основі розрахунків, зважаючи на режими роботи і точну номенклатуру елементів системи, а також результати експериментів над моделями, макетами, дослідними та промисловими зразками. Розробляється програмне забезпечення системи, проводиться його перевірка та діагностування за тестами і шляхом імітаційного моделювання на моделі системи, яка проектується. З метою забезпечення надійності здійснюють виявлення та виправлення всіх помилок в документації, яка розробляється. | |
| − | + | *Етап виробництва | |
| − | + | Основним є технічний контроль, який охоплює всі стадії виробничого процесу, починаючи від вхідного конгролю якості матеріалів, які надходять, і комплектуючих виробів, включаючи контроль якості та відповідність технічній документації виготовлених друкованих плат, блоків, пристроїв, схемних з’єднань, конструкції, і закінчуючи випробуваннями готової продукції. Виявляються недоліки в розробці, які впливають на надійність системи, та приймаються заходи з метою їх усунення. | |
| − | + | *Етап експлуатації | |
| − | + | На цьому етапі здійснюється контроль та забезпечення умов навколишнього середовища, які передбачаються проектом, забезпечення достатньої кваліфікації та необхідного складу обслуговуючого персоналу, організація та проведення техобслуговування і ремонтів. Продовжується збирання інформації про відмови апаратури і програмного забезпечення, які передаються розробникам з метою усунення причин відмов. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
==== Локальні оптоволоконні мережі для передачі голосу ==== | ==== Локальні оптоволоконні мережі для передачі голосу ==== | ||
| − | Оптичні кабелі - одне з останніх досягнень сучасної технології. Телекомунікаційні мережі всього світу переводяться на використання цієї техніки (дивись, наприклад, T. Flanagan, "Fiber Network Survivability" IEEE Communication Magazine 28 (1990) 46-53). Основною перевагою оптичного середовища передачі в порівнянні з передачею по мідних кабелях є істотне зростання пропускної спроможності та зниження рівня шумів. Саме з цієї причини багато | + | Оптичні кабелі - одне з останніх досягнень сучасної технології. Телекомунікаційні мережі всього світу переводяться на використання цієї техніки (дивись, наприклад, T. Flanagan, "Fiber Network Survivability" IEEE Communication Magazine 28 (1990) 46-53). Основною перевагою оптичного середовища передачі в порівнянні з передачею по мідних кабелях є істотне зростання пропускної спроможності та зниження рівня шумів. Саме з цієї причини багато телефонних мереж загального користування здійснюють швидкий перехід на оптику. Як, проте, виявилося, у проблематиці надійності мереж існують більш важливі проблеми, і саме їх потрібно вивчати. А саме: пропускна здатність оптоволоконних мереж надзвичайно висока, тому структура таких мереж, на відміну від звичайних, має більш розподілений характер. Старі мережі були більш розгалуженими і мали велике число зв'язків, питання мережевої надійності стояло не так гостро. При проектуванні сучасних мереж слід серйозно поставитися до проблеми мережевий надійності, тому що перебої в роботі навіть одного з оптичних каналів можуть викликати розрив мережі. |
| − | До оптичних | + | До оптичних каналів додають канали-дублери з можливістю перемикання між основним і дублюючим каналом. При цьому бажано, щоб траси їх прокладки не збігалися (по країні нишпорять бульдозери та екскаватори, так і норовлять порвати будь-які кабелі). У результаті ми зможемо застосувати до оптичної мережі вже існуючі методи оцінки надійності. |
| − | ==== | + | ==== Архітектури перемикачів і комп'ютерів, стійкі до збоїв ==== |
| − | Комп'ютерна система називається стійкою до збоїв, якщо при відмові одного з її компонентів вона продовжує функціонувати. У 1970-х роках такі комп'ютери використовувалися як | + | Комп'ютерна система називається стійкою до збоїв, якщо при відмові одного з її компонентів вона продовжує функціонувати. У 1970-х роках такі комп'ютери використовувалися як перемикачі в опорних телекомунікаційних мережах. І сьогодні вони широко застосовуються у багатьох додатках. Пізніше були розроблені паралельні обчислювальні архітектури. З метою підвищення продуктивності паралельні ЕОМ збиралися з безлічі однотипних елементів. Однак паралельні архітектури мають також і підвищені характеристики надійності. Зазвичай такі відмовостійкі і паралельні комп'ютерні системи при аналізі надійності моделювались як мережі. Оскільки більша частина досліджень з оцінки мережевої надійності велася для мереж передачі даних, основний упор робився на алгоритми аналізу топології мереж. Стимулом робіт з мережевої надійності послужили комп'ютерні архітектури, в основі роботи яких лежать сильно структуровані мережі, поєднані з певними архітектурами ЕОМ. Зазвичай використовуються заходи, що базуються на пов'язаності мережі. Проте особливо у випадку паралельних ЕОМ з великою кількістю процесорів повинні розглядатися параметри надійності, які враховують міркування пропускної здатності. |
==== Інші застосування ==== | ==== Інші застосування ==== | ||
| Рядок 75: | Рядок 50: | ||
==== Причини виникнення збоїв ==== | ==== Причини виникнення збоїв ==== | ||
| − | Механізми втрат і причини їх виникнення відносно добре вивчені в класичній теорії надійності. Наприклад, в електронних системах деградація вузлів відбувається, коли вони піддаються безперервному теплового впливу. У результаті такі вузли випадковим чином виходять з ладу. Аналіз надійності для подібних систем звичайно включає в себе вивчення цих випадкових процесів і параметри їх розподілів. При аналізі | + | Механізми втрат і причини їх виникнення відносно добре вивчені в класичній теорії надійності. Наприклад, в електронних системах деградація вузлів відбувається, коли вони піддаються безперервному теплового впливу. У результаті такі вузли випадковим чином виходять з ладу. Аналіз надійності для подібних систем звичайно включає в себе вивчення цих випадкових процесів і параметри їх розподілів. При аналізі мережевої надійності частина механізмів, що викликають втрати, відомі також як і параметри їх функцій розподілу. Але залишається багато не менш важливих механізмів, про функції розподілу яких ми нічого не можемо сказати. Наприклад, існує багато публікацій про виникнення відмов у роботі оптоволоконних мереж, викликаних природними причинами, такими, як пожежі, або помилками оператора транзитної мережі, який спільно використовував канал. Таким чином, важко побудувати модель збоїв в каналі, що задовольняє реальній частоті збоїв. Зазвичай, прогноз частоти збоїв у мережі будується на основі історичного аналізу або результатів вимірювань. Більш докладний розгляд проблеми представлено в книзі MO Ball, C.J. Colbourn, J.S. Provan, "Network Reliability". |
=== Основні визначення === | === Основні визначення === | ||
| Рядок 93: | Рядок 68: | ||
Визначення надійності компоненту не враховує час відновлення. Специфікується проміжок часу t, а надійність компонента визначається як імовірність того, що за цей час t компонент залишиться в робочому стані. Допускаються також інші трактування для ймовірності того, що компонент працює. Звичайно, інтерпретація рівня надійності компонента визначає у свою чергу інтерпретацію заходів мережевий надійності. У решти статті ми будемо використовувати ймовірність працездатності або надійності і не будемо намагатися це як-небудь інтерпретувати. | Визначення надійності компоненту не враховує час відновлення. Специфікується проміжок часу t, а надійність компонента визначається як імовірність того, що за цей час t компонент залишиться в робочому стані. Допускаються також інші трактування для ймовірності того, що компонент працює. Звичайно, інтерпретація рівня надійності компонента визначає у свою чергу інтерпретацію заходів мережевий надійності. У решти статті ми будемо використовувати ймовірність працездатності або надійності і не будемо намагатися це як-небудь інтерпретувати. | ||
| − | За відправну точку приймемо мережа G = (V, E), в якій V - набір вузлів або вершин, а Е - набір неорієнтованих ребер або набір орієнтованих дуг | + | За відправну точку приймемо мережа ''G=(V,E)'', в якій ''V'' - набір вузлів або вершин, а ''Е'' - набір неорієнтованих ребер або набір орієнтованих дуг. При вивченні простих моделей потоків (найкоротших шляхів), ми асоціюємо пропускну здатність <span class="texample">с<sub>е</sub></span>(расстояние <span class="texample">d<sub>е</sub></span>) з кожним її елементом. Ми інтерпретуємо <span class="texample">р<sub>е</sub></span>, як імовірність того, що <span class="texample">е</span> працює і має пропускну здатність <span class="texample">с<sub>е</sub></span> (відстань <span class="texample">d<sub>е</sub></span>), а <span class="texample">1-р<sub>е</sub></span> - як ймовірність того, що <span class="texample">е</span> не працює і має пропускну здатність 0 (відстань дорівнює нескінченності). |
| − | Іноді, при вивченні | + | Іноді, при вивченні ''мережевої надійності'', буває зручно переходити до узагальнених випадків і розглядати когерентні виконавчі системи. Стохастична бінарна система '''SBS'''(stochastic binary system) - являє собою систему, яка відмовляє випадковим чином в результаті випадкового виходу з ладу її компонента. Кожен компонент з набору мережевих компонентів ''T'' може приймати одне з двох значень: ''працює'', ''не працює''. Структура системи описується функцією ''ψ(S)'', визначеної для S⊆T: |
[[Файл:Qqq.png]] | [[Файл:Qqq.png]] | ||
| − | Функція SBS є когерентної, якщо (Т) = 1, (0) = 0 і виконується умова (S ') (S) для S' | + | Функція '''SBS''' є когерентної, якщо ψ(Т)=1, ψ(0)=0 і виконується умова ψ(S^')≥ψ(S)для S^'⊃S. Остання властивість означає, що вихід з ладу будь-якого з компонентів може тільки зашкодити роботі системи. Представляє інтерес задачу обчислення виразу: |
| − | Rel (SBS, p) = Pr [(S) = 1], де S - набір працюючих компонентів, | + | Rel(SBS,p)=Pr[ψ(S)=1], де S - набір працюючих компонентів, |
| − | якщо відомий вид розподілу (). Іноді ми розглядаємо завдання надійності, де | + | якщо відомий вид розподілу ψ(). Іноді ми розглядаємо завдання надійності, де <span class="texample">р<sub>е</sub>=p</span> для всех <span class="texample">е</span>, в цих випадках ми замінюємо <span class="texample">p</span> на <span class="texample">p</span> у поданій вище нотації. Для довільної стохастичною когерентної двійкової системи (''SCBS - stochastic coherent binary system'') визначимо набір шляхів як набір компонентів, працездатність яких означає роботу системи в цілому. Назвемо мініпроходом мінімальний набір шляхів, що забезпечують працездатність системи. Аналогічно визначимо набір розрізів як набір компонентів, чия відмова викличе відмова системи, а мініразрезом назвемо мінімальний набір таких розрізів. |
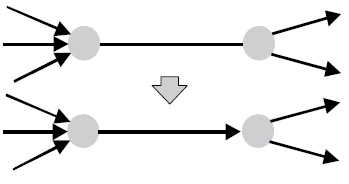
| − | У багатьох додатках можуть відмовляти як дуги, так і вузли. Отже, доводиться вивчати моделі, здатні реагувати і на відмови вузлів, і на обриви дуг. На щастя, для випадку орієнтованих мереж за допомогою перетворення, показаного на малюнку | + | У багатьох додатках можуть відмовляти як дуги, так і вузли. Отже, доводиться вивчати моделі, здатні реагувати і на відмови вузлів, і на обриви дуг. На щастя, для випадку орієнтованих мереж за допомогою перетворення, показаного на малюнку, завдання з ненадійними ребрами і вузлами можна звести до задачі з абсолютно надійними вузлами і ненадійними ребрами. У кожному разі дуга, яка заміняє вузли, успадковує характеристики відповідних вузлів. |
[[Файл:Rtrt.jpg]] | [[Файл:Rtrt.jpg]] | ||
| − | |||
| − | |||
| − | |||
=== Складність аналізу мережевої надійності === | === Складність аналізу мережевої надійності === | ||
| − | + | Існує два важливих окремих випадків мір: ''2-термінальна міра'' з ''|К|=2'' і всетермінальная міра, де ''К = V''. Ці заходи прийнято позначати ''Rel2(G,s,p)і RelА (G,s,p)'', відповідно ''(Rel - надійність)''. | |
| + | Наведемо результати, отримані для складності аналізу мережевої надійності в трьох частинних задачах: ''k-термінальної'' ''2-термінальної'' і ''всетермінальної''. | ||
| + | |||
==== k терміналів ==== | ==== k терміналів ==== | ||
| − | + | Набір шляхів з мінімальною потужністю для ''k-термінальної'' міри є дерево Штейнера з мінімальною потужністю. Відомо, що завдання розпізнавання є ''NP'' складною для орієнтованих і неорієнтованих мереж. Аналіз функціональної і раціональної надійності для задачі аналізу мають ''NP'' складність. Валіант [LGValiant, "The complexity the enumeration and reliability problems", SIAM, J. Computing, 8 (1979), 410-421] наводить альтернативне доказ, що полягає в демонстрації того, що обчислення | |
| − | + | ||
| − | + | ||
| − | + | ||
| + | ''SN(K)=ΣFi=|(S:S відповідає субграфу, який містить шлях до кожного вузла в К)|'', має складність NP. Тут K є набором терміналів. | ||
| − | + | ==== 2 термінала ==== | |
| + | Завдання розпізнавання мінімального набору шляхів і розрізів, поєднані з ''2-термінальної'' мірою, є проблемами найкоротшого шляху і мінімального розрізу, відповідно. Відомі поліноміальні алгоритми для обох цих завдань. Валіант вперше показав, що завдання аналізу надійності в разі ''2-термінальної'' міри мають складність ''NP''. Його результатом служать гарною ілюстрацією методик, які використовуються в даній області. | ||
| − | + | ==== Всетермінальная міра ==== | |
| + | Для орієнтованої всетермінальной міри проблеми з наборами шляхів і розрізів з мінімальною потужністю є завданням пошуку мінімального покриває дерева і мінімального s-орієнтованого розрізу, відповідно. | ||
| − | + | Обидві ці завдачі вирішуються за поліноміальний час. Завдання підрахунку мінімальних s-орієнтованих розрізів має складність ''NP''. А це, у свою чергу, означає, що пов'язана з нею завдача надійності має складність ''NP''. Для випадку неорієнтованому заходи задачі з розпізнавання і підрахунку мінімального набору шляхів і розрізів мають поліноміальну складність. Однак завдання обчислення загального члена в полінома надійності має складність ''NP'', тому що завдача аналізу надійності для неорієнтованого випадку мають складність ''NP''. | |
| − | + | У світлі цих негативних результатів, більшість досліджень мали на меті аналіз структурованих мереж. Найширший клас мереж, для яких можна виконати обчислення за поліноміальний час, базується на послідовно-паралельних графах і певних узагальненнях. Прован ''(JSProvan, "The complexity of reliability computations in planar and acyclic graphs", SIAM, J. Computings 8 (1986), 694-702)'' показав, що неорієнтована 2-термінальна проблема надійності має складність ''NP'' в планарних нециклічних мережах, що мають ступеня вузлів не вище трьох. | |
| − | . | + | Результати даного розділу вказують на те, що поліноміальні алгоритми для мережевої надійності існують тільки для маленького класу мереж. Завдяки цьому факту велике число досліджень присвячене вивченню обмежень мережевий надійності і підходів, заснованих на методі ''Монте-Карло''. |
| − | + | Рішення задач оцінки надійності спирається на просте, але важливе міркування: існує таке перетворення графа, яке не змінює значень різних заходів надійності, і це перетворення може бути використано для спрощення топології мережі, для якої потрібно обчислити точне значення надійності. Наша перша мета - перетворення графів, які призводять до спрощення. | |
| + | Ребро або дуга, які не входять ні в один з мінімальних наборів шляхів, називається нерелевантні: працездатність таких нерелевантних ребер не впливає на роботу або відмову мережі. Найпростішим способом спрощує перетворення графа є видалення нерелевантних ребер. За визначенням, таке перетворення не змінює міру надійності. Щоб перетворення мало практичне застосування для мережі, час його ефективної реалізації має бути поліноміальним. Для все-, ''k''-і ''2-термінальних'' мір надійності петлі завжди є нерелевантними. А для ''k''-і ''2 - термінальних'' мір надійності нерелевантними є також усі кінцеві ребра, що не мають термінального закінчення. Такі ребра легко знаходити і видаляти. У разі орієнтованих задач надійності пошук нерелевантних дуг аж ніяк не просте завдання. Було показано, що задача знаходження нерелевантних дуг у випадку ''(s,t)-пов'язаності'' має складність ''NP'', в той час як загальна неорієнтована завдання допускає ефективне рішення. | ||
| − | + | Проблема мережевої надійності досліджується досить давно. В даний час ясно, що точного рішення навіть для мереж обмеженого розміру це завдання не вирішено. Але можна вже сьогодні, якщо потрібно, провести оцінку надійності зверху і знизу. Варто, втім, мати на увазі, що навіть це вимагає досить складних розрахунків. | |
| − | + | ||
'''Поняття надійності''' | '''Поняття надійності''' | ||
| − | |||
| − | |||
Наді́йність — властивість технічних об'єктів зберігати у часі у встановлених межах значення всіх параметрів, необхідних для виконання технічних (технологічних та ін.) функцій в заданих режимах і умовах застосування. Під технологічними об'єктами розуміють пристрої, прилади, механізми, машини, комплекси обладнання, буд. конструкції і споруди, технол. операції і процеси, системи зв'язку, інформаційні системи, автоматизов. системи управління технол. процесами тощо. | Наді́йність — властивість технічних об'єктів зберігати у часі у встановлених межах значення всіх параметрів, необхідних для виконання технічних (технологічних та ін.) функцій в заданих режимах і умовах застосування. Під технологічними об'єктами розуміють пристрої, прилади, механізми, машини, комплекси обладнання, буд. конструкції і споруди, технол. операції і процеси, системи зв'язку, інформаційні системи, автоматизов. системи управління технол. процесами тощо. | ||
| − | |||
'''Типи відмов''' | '''Типи відмов''' | ||
| − | |||
Мережу Інтернет (спочатку відому під назвою ARPANET) було створено | Мережу Інтернет (спочатку відому під назвою ARPANET) було створено | ||
| Рядок 172: | Рядок 142: | ||
практики детальних звітів зі статистикою та аналізом по окремих типах атак. | практики детальних звітів зі статистикою та аналізом по окремих типах атак. | ||
Графік росту кількості вторгнень на протязі часу показано на рис. 1. | Графік росту кількості вторгнень на протязі часу показано на рис. 1. | ||
| + | |||
| + | == Методика розрахунку надійності комп'ютерних мереж == | ||
| + | Для аналізу структурної надійності мереж зручно використовувати матрично-топологічні методи. В їхній основі лежить подання мережі за допомогою графа мережі (рис.1). Комп'ютерну мережу можна представити як сукупність множини X={x1,x2, ...,x} вузлів і множини U={uij } з'єднуючі вузли xi і xj ребер. | ||
| + | |||
| + | [[Файл:Metroznadkompmer0.PNG|Metroznadkompmer0.PNG]] | ||
| + | |||
| + | рис.1 Граф мережі | ||
| + | |||
| + | Будемо використовувати наступні основні поняття і визначення. Множина всіх вузлів графа G, суміжних з деяким вузлом xi, називається оточенням вузла xi і позначається N(xi). Ступінь вузла графа дорівнює числу ребер, інцидентних даному вузлу. Будемо позначати ступінь вузла х через deg(x). Послідовність, вузлів і ребер x1, u1, x2, u2…,xl, ul, xl+1називається маршрутом, що з'єднує вузли xl і xl+1, або (xl, xl+1)-маршрутом. Очевидно, що маршрут можна задати послідовністю x1, x2, …,xl+1 його вузлів, а також послідовністю u1, u2, …, ul ребер. Сама непересічна впорядкована послідовність ребер з вузла xs у вузол xt називається шляхом. Число ребер, що утворюють шлях називається рангом шляху. Між будь-якими двома вузлами мережі можна побудувати, як правило, множину шляхів. Шляхи називаються незалежними, якщо в них немає загальних ребер. Якщо між будь-якими двома вузлами існує не менш k незалежних шляхів, то мережа називається k-зв'язковою. Перетином мережі будемо називати мінімальну сукупність ребер, видалення яких розділить мережу на дві підмережі. Кількість ребер перетину називається рангом перетину. Перетини називаються незалежними, якщо вони не містять ті самі ребра. Нехай P1l – деякий шлях виду x1, x2, …,xl у графі G, xi і xj – вхідні в нього вузли, i < j. Очевидно, що частина xi, xi+1,…,xj шляхи P1l, що починається у вузлі xi і закінчується в xj, сама є шляхом графа G. Цей шлях будемо називати (xi, xj) – фрагментом шляху P1l. | ||
| + | |||
| + | Через відсутність прийнятної моделі механізму втрат в мережі і властивій складності розрахунку мережної надійності використовуються часові моделі з дискретною ймовірністю. Тут ми розглянемо найбільш популярну модель. В ній передбачається, що мережні компоненти (вузли і ребра мовою графів) можуть приймати лише два стани: працює або не працює. Стан мережного компонента - випадкова величина, що не залежить від стану інших компонентів (в загальному випадку це може бути і не так). Постановка задачі обчислення надійності: для кожного компонента мережі задана ймовірність того, що він перебуває в робочому стані, і потрібно обчислити міру надійності мережі. | ||
| + | |||
| + | В цьому випадку як показник надійності мережі в цілому можна використовувати ймовірність настання складної події, що полягає у встановленні зв'язків між всіма вузлами із заданої множини, і розраховувати його як відношення суми зважених коефіцієнтів важливості ймовірностей з'єднань пари вузлів. | ||
| + | |||
| + | [[Файл:Nadkompmerformzrivn1.PNG|Nadkompmerformzrivn1.PNG]] | ||
| + | |||
| + | де H0 – показник надійності всієї мережі, Кi – коефіцієнт важливості i-го з'єднання вузлів (0 Ki 1), Hi – показник надійності i-го з'єднання вузлів. | ||
| + | |||
| + | При проектуванні реальних мереж звичайно відсутня необхідність точного розрахунку надійності мережі. Проектувальникам необхідно лише переконатися в тім, що надійність мережі, з одного боку, не нижче заданої та, з іншого боку, не має економічно необґрунтованого запасу. Інакше кажучи, на практиці досить гарантувати, що дійсне значення надійності H0 перебуває в деяких межах Нтin < Н0 < Нтах. Оцінка надійності мережі із заданою кінцевою точністю дозволить скоротити трудомісткість розрахунків в тим більшій мірі, чим нижче необхідна точність оцінки. | ||
| + | Існує методика розрахунку оцінок надійності, причому нижня оцінка Hμ розраховується по сукупності всіх шляхів між вузлами, верхня ж Hσ – по сукупності перетинів. При розрахунку надійності по сукупності шляхів додавання кожного наступного шляху приводить до збільшення надійності, а при розрахунку по сукупності перетинів додавання кожного наступного перетину приводить до зменшення структурної надійності, що створює передумови для двосторонньої оцінки структурної надійності з гарантованою точністю по обмежених наборах шляхів і перетинів. Ця властивість дозволяє регулювати трудомісткість оцінок надійності залежно від заданої точності. | ||
| + | |||
| + | Дійсно, для вирішення задачі досить послідовно переглядати шляхи μ, поки не виконається умова Hμ(m) ≥ Hmin і потім переглядати перетини σ, поки не виконається умова Hσ(r) ≤ Hmax. Тут m, r – число шляхів і перетинів відповідно. Якщо для деякого т виявиться, що Hμ(m) > Hmax, то можна припинити розрахунки і прийняти рішення, що в мережі закладена зайва надмірність, а якщо для деякого r виявиться, що Hσ(r) < Hmin , то це значить, що вимоги до надійності мережі не виконуються. Кількість потребуючого перегляду шляхів т і перетинів r звичайно набагато менше загального числа шляхів n і загального числа перетинів k графа, чим і досягається скорочення трудомісткості оцінки. Одночасно гарантується, що значення показника надійності мережі лежить в заданих межах Hμ(m) < H0 < Hσ(r) . | ||
| + | |||
| + | В такий спосіб для виконання розрахунків необхідний список всіх можливих шляхів і перетинів між заданими вузлами xa і xb. З літератури відомо, що шукана надійність з'єднання Нab залежить від надійності кожного шляху і варіантів їхніх перетинів по загальних ребрах. Якщо враховувати тільки незалежні шляхи, то трудомісткість обчислень значно скорочується. Аналогічна ситуація з незалежними перетинами. | ||
| + | Нехай надійність j-го ребра i-го шляху - . Тоді надійність i-го шляху буде дорівнювати: | ||
| + | |||
| + | [[Файл:Nadkompmerformzrivn2.PNG|Nadkompmerformzrivn2.PNG]] | ||
| + | |||
| + | де mi -ранг шляху. | ||
| + | |||
| + | Якщо всі шляхи незалежні, то ймовірність зв’язності вузлів xa і xb по множині незалежних шляхів можна визначити як | ||
| + | |||
| + | [[Файл:Nadkompmerformzrivn3.PNG|Nadkompmerformzrivn3.PNG]] | ||
| + | |||
| + | де n – кількість незалежних шляхів між xa і xb. | ||
| + | |||
| + | Оскільки для підвищення точності оцінки необхідно максимізувати , то необхідно максимізувати число незалежних шляхів при одночасній мінімізації їхніх рангів. | ||
| + | |||
| + | Міркуючи аналогічно, неважко встановити, що для збільшення точності верхньої оцінки ймовірності зв’язаності вузлів по множині незалежних перетинів потрібно максимізувати число незалежних перетинів при мінімізації їхніх рангів. | ||
| + | Проблема мережної надійності досліджується досить давно. В цей час ясно, що точного рішення навіть для мереж обмеженого розміру ця задача не має. Але можна вже сьогодні, якщо потрібно, зробити оцінку надійності зверху і знизу. Треба, втім, мати на увазі, що навіть це вимагає досить складних розрахунків. | ||
| + | |||
| + | |||
| + | [[category:Комп'ютерні мережі]] | ||
Поточна версія на 17:02, 7 березня 2021
Зміст
Основні визначення
Забезпечення надійності комп’ютерних систем здійснюється в двох напрямах. В першому випадку забезпечення надійності комп’ютерних систем визначається відсутністю відмов, збоїв, помилок та несправностей. В другому - можливістю швидкого відновлення апаратури та обчислювального процесу.
Надійність можна визначити як властивість об’єкта зберігати в часі у визначених межах значення всіх параметрів, іцо характеризують спроможність виконувати потрібні функції в заданих режимах і умовах застосування, технічного обслуговування, ремонтів, зберігання та транспортування. Надійність сама по собі - складна властивість, яка в залежності від призначення об’єкта та умов його експлуатації складається із сполучень властивостей: безвідмовності, довговічності, ремонтопридатності та збережності.
Безвідмовність - це властивість об'єкта безперервно зберігати працездатний стан в проміжку деякого часу або деякого напрацювання.
Напрацювання - це об’єм (час) роботи об'єкта. Може визначатися в іншій формі, наприклад, кількості вирішених задач або циклів роботи.
Відмова - подія, яка являє собою порушення працездатності об'єкта. Вона в основному викликається фізичним руйнуванням елементів або поступовим погіршенням їх характеристик.
Збій - короткочасне порушення правильної роботи обчислювального пристрою або його елемента, після якого його працездатність самовідновлюється або відновлюється оператором без проведення ремонту. Збої можуть бути викликані внутрішніми або зовнішніми перешкодами.
Відновлення комп'ютерних систем — це приведення апаратури в працездатний стан шляхом заміни окремих елементів, які відмовили. Основні якості обчислювальної техніки, пов’язані з її надійністю, описуються розподіленням відмов в часі, процесами відновлення та організацією обслуговування. Покращання надійності потребує додаткових витрат на розробку, виготовлення та експлуатацію систем. При встановленні вимог до надійності обчислювальної техніки необхідно зважати на витрати, пов'язані з її розробкою та виготовленням, витрати на персонал, зайнятий ремонтом і обслуговуванням, виграти, які визначаються наслідками відмов та простоїв, зниженням ефективності або продуктивності системи, а також витрати, пов’язані із збільшенням маси або габаритів системи та ін. Якщо відмова комп’ютерних систем може спричинити собою небезпеку для життя людей або аварію, то рівень надійності визначається з такої вимоги, щоб ймовірність відмови відповідала практично неможливій події.
Методи забезпечення надійності на етапах життєвого циклу комп'ютерних систем
- Етап складання технічного завдання
На даному етапі збирають всі дані, які є, про аналогічні та близькі системи, дані про умови застосування комп’ютерних систем і вимоги, що висуваються до функцій, які виконуються розглянутою системою. За сукупністю цих даних і вимог розробляються основні вимоги до надійності нової системи.
- Етап ескізного проектування
На цьому етапі обирається елементна база і визначаються особливості структури, архітектури та організації системи, яка розробляється. За цими даними проводиться попередній розрахунок надійності, виявляються найменш надійні підсистеми, і на цій основі приймається рішення про резервування системи, а також рішення про засоби та організацію технічного обслуговування, тобто профілактичні та ремонтні роботи. Досліджується питання про доцільність резервування і методи автоматичного відновлення та підвищення відмовостійкості системи.
- Етап технічного і робочого проектування
Під час виконання даного етапу перевіряються та уточнюються раніше прийняті рішення. Для цього використовують уточнені дані про надійність, отримані на основі розрахунків, зважаючи на режими роботи і точну номенклатуру елементів системи, а також результати експериментів над моделями, макетами, дослідними та промисловими зразками. Розробляється програмне забезпечення системи, проводиться його перевірка та діагностування за тестами і шляхом імітаційного моделювання на моделі системи, яка проектується. З метою забезпечення надійності здійснюють виявлення та виправлення всіх помилок в документації, яка розробляється.
- Етап виробництва
Основним є технічний контроль, який охоплює всі стадії виробничого процесу, починаючи від вхідного конгролю якості матеріалів, які надходять, і комплектуючих виробів, включаючи контроль якості та відповідність технічній документації виготовлених друкованих плат, блоків, пристроїв, схемних з’єднань, конструкції, і закінчуючи випробуваннями готової продукції. Виявляються недоліки в розробці, які впливають на надійність системи, та приймаються заходи з метою їх усунення.
- Етап експлуатації
На цьому етапі здійснюється контроль та забезпечення умов навколишнього середовища, які передбачаються проектом, забезпечення достатньої кваліфікації та необхідного складу обслуговуючого персоналу, організація та проведення техобслуговування і ремонтів. Продовжується збирання інформації про відмови апаратури і програмного забезпечення, які передаються розробникам з метою усунення причин відмов.
Локальні оптоволоконні мережі для передачі голосу
Оптичні кабелі - одне з останніх досягнень сучасної технології. Телекомунікаційні мережі всього світу переводяться на використання цієї техніки (дивись, наприклад, T. Flanagan, "Fiber Network Survivability" IEEE Communication Magazine 28 (1990) 46-53). Основною перевагою оптичного середовища передачі в порівнянні з передачею по мідних кабелях є істотне зростання пропускної спроможності та зниження рівня шумів. Саме з цієї причини багато телефонних мереж загального користування здійснюють швидкий перехід на оптику. Як, проте, виявилося, у проблематиці надійності мереж існують більш важливі проблеми, і саме їх потрібно вивчати. А саме: пропускна здатність оптоволоконних мереж надзвичайно висока, тому структура таких мереж, на відміну від звичайних, має більш розподілений характер. Старі мережі були більш розгалуженими і мали велике число зв'язків, питання мережевої надійності стояло не так гостро. При проектуванні сучасних мереж слід серйозно поставитися до проблеми мережевий надійності, тому що перебої в роботі навіть одного з оптичних каналів можуть викликати розрив мережі.
До оптичних каналів додають канали-дублери з можливістю перемикання між основним і дублюючим каналом. При цьому бажано, щоб траси їх прокладки не збігалися (по країні нишпорять бульдозери та екскаватори, так і норовлять порвати будь-які кабелі). У результаті ми зможемо застосувати до оптичної мережі вже існуючі методи оцінки надійності.
Архітектури перемикачів і комп'ютерів, стійкі до збоїв
Комп'ютерна система називається стійкою до збоїв, якщо при відмові одного з її компонентів вона продовжує функціонувати. У 1970-х роках такі комп'ютери використовувалися як перемикачі в опорних телекомунікаційних мережах. І сьогодні вони широко застосовуються у багатьох додатках. Пізніше були розроблені паралельні обчислювальні архітектури. З метою підвищення продуктивності паралельні ЕОМ збиралися з безлічі однотипних елементів. Однак паралельні архітектури мають також і підвищені характеристики надійності. Зазвичай такі відмовостійкі і паралельні комп'ютерні системи при аналізі надійності моделювались як мережі. Оскільки більша частина досліджень з оцінки мережевої надійності велася для мереж передачі даних, основний упор робився на алгоритми аналізу топології мереж. Стимулом робіт з мережевої надійності послужили комп'ютерні архітектури, в основі роботи яких лежать сильно структуровані мережі, поєднані з певними архітектурами ЕОМ. Зазвичай використовуються заходи, що базуються на пов'язаності мережі. Проте особливо у випадку паралельних ЕОМ з великою кількістю процесорів повинні розглядатися параметри надійності, які враховують міркування пропускної здатності.
Інші застосування
Існує велика різноманітність мережевих моделей, частина з них застосовується в інших галузях науки. У всіх аналізованих випадках мережа підтримує роботу багатьох користувачів, трафік кожного з них потрібно через мережу одним або кількома маршрутами. Зазвичай мається на увазі, що можна зробити більш точну оцінку надійності, якщо врахувати в розрахунках параметри маршрутизації. На завершення потрібно відзначити, що потрібно враховувати величини пропускної здатності. Одна з найбільш цікавих галузей застосування - міські мережі наземного транспорту. У цьому контексті інциденти, такі, як аварії на автомагістралях, викликають відмову мережевих вузлів або дуг. Хоча порушення зв'язаності в мережі міського транспорту відбуваються дуже рідко, все-таки цілком типово, коли відмова сайту або зв'язку викликає ситуацію значною перевантаження.
Нарешті, застосування багатьох засобів оцінки надійності мережі, які розроблені для заходів, що базуються на зв'язності, поширюється на зовсім інші проблеми надійності, наприклад, у сфері диспетчеризації та розподілу ресурсів (в тому числі операційних систем або мереж електропостачання).
Причини виникнення збоїв
Механізми втрат і причини їх виникнення відносно добре вивчені в класичній теорії надійності. Наприклад, в електронних системах деградація вузлів відбувається, коли вони піддаються безперервному теплового впливу. У результаті такі вузли випадковим чином виходять з ладу. Аналіз надійності для подібних систем звичайно включає в себе вивчення цих випадкових процесів і параметри їх розподілів. При аналізі мережевої надійності частина механізмів, що викликають втрати, відомі також як і параметри їх функцій розподілу. Але залишається багато не менш важливих механізмів, про функції розподілу яких ми нічого не можемо сказати. Наприклад, існує багато публікацій про виникнення відмов у роботі оптоволоконних мереж, викликаних природними причинами, такими, як пожежі, або помилками оператора транзитної мережі, який спільно використовував канал. Таким чином, важко побудувати модель збоїв в каналі, що задовольняє реальній частоті збоїв. Зазвичай, прогноз частоти збоїв у мережі будується на основі історичного аналізу або результатів вимірювань. Більш докладний розгляд проблеми представлено в книзі MO Ball, C.J. Colbourn, J.S. Provan, "Network Reliability".
Основні визначення
Через відсутність прийнятної моделі механізму втрат в мережі і властивої складності розрахунку мережевий надійності використовуються времязавісімие моделі з дискретною ймовірністю. Тут ми розглянемо найбільш популярну модель. У ній передбачається, що мережеві компоненти (вузли та ребра на мові графів) можуть приймати лише два стани: працює чи не працює. Стан мережевого компонента - випадкова величина, яка не залежить від стану інших компонентів (у загальному випадку це може бути і не так). Постановка завдання обчислення надійності: для кожного компонента мережі задана ймовірність того, що він знаходиться в робочому стані, і потрібно обчислити міру надійності мережі.
Розглянемо якесь узагальнення цієї моделі. Зокрема, будемо розглядати моделі, в яких кожен компонент може знаходитися в одному з декількох станів, або моделі, в яких робочий стан характеризується чисельною значенням. Чисельні значення цих характеристик зазвичай прирівнюються метриці відстані або величиною пропускної здатності. Проста модель з двома станами добре підходить для обчислення заходи пов'язаності. Коли виникає необхідність порахувати більш складну міру, наприклад, продуктивність системи, застосовують більш складні характеристики станів компонентів.
Для моделі з двома станами ймовірність працездатності компонента або, простіше, надійність, можна розуміти по-різному. Найбільш поширеними є формулювання:
1. доступність компонента; 2. надійність компонента.
Взагалі в цьому розділі домовимося застосовувати термін надійність для позначення ймовірності того, що компонент або система працює. Тут ми обговорюємо більш окрему ухвалу. Доступність використовується в контексті ремонтоспособних систем. Зі сказаного випливає, що компонент може знаходитися в одному з трьох станів: працює, не працює, у процесі відновлення. Доступність компонента визначається як ймовірність його роботи у випадковий момент часу. Оцінка величини доступності проводиться з урахуванням середнього часу відновлення в робочий стан і середнього часу в неробочому стані. Надійність можна записати так:
Визначення надійності компоненту не враховує час відновлення. Специфікується проміжок часу t, а надійність компонента визначається як імовірність того, що за цей час t компонент залишиться в робочому стані. Допускаються також інші трактування для ймовірності того, що компонент працює. Звичайно, інтерпретація рівня надійності компонента визначає у свою чергу інтерпретацію заходів мережевий надійності. У решти статті ми будемо використовувати ймовірність працездатності або надійності і не будемо намагатися це як-небудь інтерпретувати.
За відправну точку приймемо мережа G=(V,E), в якій V - набір вузлів або вершин, а Е - набір неорієнтованих ребер або набір орієнтованих дуг. При вивченні простих моделей потоків (найкоротших шляхів), ми асоціюємо пропускну здатність се(расстояние dе) з кожним її елементом. Ми інтерпретуємо ре, як імовірність того, що е працює і має пропускну здатність се (відстань dе), а 1-ре - як ймовірність того, що е не працює і має пропускну здатність 0 (відстань дорівнює нескінченності).
Іноді, при вивченні мережевої надійності, буває зручно переходити до узагальнених випадків і розглядати когерентні виконавчі системи. Стохастична бінарна система SBS(stochastic binary system) - являє собою систему, яка відмовляє випадковим чином в результаті випадкового виходу з ладу її компонента. Кожен компонент з набору мережевих компонентів T може приймати одне з двох значень: працює, не працює. Структура системи описується функцією ψ(S), визначеної для S⊆T:
Функція SBS є когерентної, якщо ψ(Т)=1, ψ(0)=0 і виконується умова ψ(S^')≥ψ(S)для S^'⊃S. Остання властивість означає, що вихід з ладу будь-якого з компонентів може тільки зашкодити роботі системи. Представляє інтерес задачу обчислення виразу:
Rel(SBS,p)=Pr[ψ(S)=1], де S - набір працюючих компонентів,
якщо відомий вид розподілу ψ(). Іноді ми розглядаємо завдання надійності, де ре=p для всех е, в цих випадках ми замінюємо p на p у поданій вище нотації. Для довільної стохастичною когерентної двійкової системи (SCBS - stochastic coherent binary system) визначимо набір шляхів як набір компонентів, працездатність яких означає роботу системи в цілому. Назвемо мініпроходом мінімальний набір шляхів, що забезпечують працездатність системи. Аналогічно визначимо набір розрізів як набір компонентів, чия відмова викличе відмова системи, а мініразрезом назвемо мінімальний набір таких розрізів.
У багатьох додатках можуть відмовляти як дуги, так і вузли. Отже, доводиться вивчати моделі, здатні реагувати і на відмови вузлів, і на обриви дуг. На щастя, для випадку орієнтованих мереж за допомогою перетворення, показаного на малюнку, завдання з ненадійними ребрами і вузлами можна звести до задачі з абсолютно надійними вузлами і ненадійними ребрами. У кожному разі дуга, яка заміняє вузли, успадковує характеристики відповідних вузлів.
Складність аналізу мережевої надійності
Існує два важливих окремих випадків мір: 2-термінальна міра з |К|=2 і всетермінальная міра, де К = V. Ці заходи прийнято позначати Rel2(G,s,p)і RelА (G,s,p), відповідно (Rel - надійність). Наведемо результати, отримані для складності аналізу мережевої надійності в трьох частинних задачах: k-термінальної 2-термінальної і всетермінальної.
k терміналів
Набір шляхів з мінімальною потужністю для k-термінальної міри є дерево Штейнера з мінімальною потужністю. Відомо, що завдання розпізнавання є NP складною для орієнтованих і неорієнтованих мереж. Аналіз функціональної і раціональної надійності для задачі аналізу мають NP складність. Валіант [LGValiant, "The complexity the enumeration and reliability problems", SIAM, J. Computing, 8 (1979), 410-421] наводить альтернативне доказ, що полягає в демонстрації того, що обчислення
SN(K)=ΣFi=|(S:S відповідає субграфу, який містить шлях до кожного вузла в К)|, має складність NP. Тут K є набором терміналів.
2 термінала
Завдання розпізнавання мінімального набору шляхів і розрізів, поєднані з 2-термінальної мірою, є проблемами найкоротшого шляху і мінімального розрізу, відповідно. Відомі поліноміальні алгоритми для обох цих завдань. Валіант вперше показав, що завдання аналізу надійності в разі 2-термінальної міри мають складність NP. Його результатом служать гарною ілюстрацією методик, які використовуються в даній області.
Всетермінальная міра
Для орієнтованої всетермінальной міри проблеми з наборами шляхів і розрізів з мінімальною потужністю є завданням пошуку мінімального покриває дерева і мінімального s-орієнтованого розрізу, відповідно.
Обидві ці завдачі вирішуються за поліноміальний час. Завдання підрахунку мінімальних s-орієнтованих розрізів має складність NP. А це, у свою чергу, означає, що пов'язана з нею завдача надійності має складність NP. Для випадку неорієнтованому заходи задачі з розпізнавання і підрахунку мінімального набору шляхів і розрізів мають поліноміальну складність. Однак завдання обчислення загального члена в полінома надійності має складність NP, тому що завдача аналізу надійності для неорієнтованого випадку мають складність NP.
У світлі цих негативних результатів, більшість досліджень мали на меті аналіз структурованих мереж. Найширший клас мереж, для яких можна виконати обчислення за поліноміальний час, базується на послідовно-паралельних графах і певних узагальненнях. Прован (JSProvan, "The complexity of reliability computations in planar and acyclic graphs", SIAM, J. Computings 8 (1986), 694-702) показав, що неорієнтована 2-термінальна проблема надійності має складність NP в планарних нециклічних мережах, що мають ступеня вузлів не вище трьох.
Результати даного розділу вказують на те, що поліноміальні алгоритми для мережевої надійності існують тільки для маленького класу мереж. Завдяки цьому факту велике число досліджень присвячене вивченню обмежень мережевий надійності і підходів, заснованих на методі Монте-Карло.
Рішення задач оцінки надійності спирається на просте, але важливе міркування: існує таке перетворення графа, яке не змінює значень різних заходів надійності, і це перетворення може бути використано для спрощення топології мережі, для якої потрібно обчислити точне значення надійності. Наша перша мета - перетворення графів, які призводять до спрощення.
Ребро або дуга, які не входять ні в один з мінімальних наборів шляхів, називається нерелевантні: працездатність таких нерелевантних ребер не впливає на роботу або відмову мережі. Найпростішим способом спрощує перетворення графа є видалення нерелевантних ребер. За визначенням, таке перетворення не змінює міру надійності. Щоб перетворення мало практичне застосування для мережі, час його ефективної реалізації має бути поліноміальним. Для все-, k-і 2-термінальних мір надійності петлі завжди є нерелевантними. А для k-і 2 - термінальних мір надійності нерелевантними є також усі кінцеві ребра, що не мають термінального закінчення. Такі ребра легко знаходити і видаляти. У разі орієнтованих задач надійності пошук нерелевантних дуг аж ніяк не просте завдання. Було показано, що задача знаходження нерелевантних дуг у випадку (s,t)-пов'язаності має складність NP, в той час як загальна неорієнтована завдання допускає ефективне рішення.
Проблема мережевої надійності досліджується досить давно. В даний час ясно, що точного рішення навіть для мереж обмеженого розміру це завдання не вирішено. Але можна вже сьогодні, якщо потрібно, провести оцінку надійності зверху і знизу. Варто, втім, мати на увазі, що навіть це вимагає досить складних розрахунків.
Поняття надійності
Наді́йність — властивість технічних об'єктів зберігати у часі у встановлених межах значення всіх параметрів, необхідних для виконання технічних (технологічних та ін.) функцій в заданих режимах і умовах застосування. Під технологічними об'єктами розуміють пристрої, прилади, механізми, машини, комплекси обладнання, буд. конструкції і споруди, технол. операції і процеси, системи зв'язку, інформаційні системи, автоматизов. системи управління технол. процесами тощо.
Типи відмов
Мережу Інтернет (спочатку відому під назвою ARPANET) було створено в 1969 р. як результат досліджень на замовлення Міністерства Оборони Сполучених Штатів Америки. Початкова мета розробки полягала у створенні відкритої мережі для обміну науковими ресурсами між вченими. Внаслідок цього було розроблено мережу на основі комутації пакетів (packet switching), яка принципово відрізнялася від відомих тоді систем комутації ліній (circuit switching), таких як телефонна мережа. Це дозволило значно підвищити гнучкість, життєздатність та масштабність, однак успіх був досягнуто ціною ослаблення безпеки. В мережі Інтернет будь-хто може надіслати будь-який пакет будь-кому, і при цьому одержувач має обробити пакет, який прийшов належним чином. Ослаблення безпеки полягає в тому, що зловмисник може вказувати в пакетах фальшиве джерело і надсилати від його імені шкідливі пакети. Тому всі системи, з’єднані з мережею Інтернет, перебувають у потен- ційній небезпеці, оскільки відкритість робить їх доступними для атакуючого. З розвитком мереж кількість фактів зловмисної діяльності почала швидко зростати. Згідно з даними CERT (Computer Emergency Response Team) , центру експертизи безпеки Інтернет, розташованому у Сполучених Штатах, кількість задокументованих випадків порушення безпеки або вторгнень стрімко зросла в 1994 р. до 137539 . Починаючи з 2004 р. CERT відмовився від підрахунку загальної кількості вторгнень і перейшов до практики детальних звітів зі статистикою та аналізом по окремих типах атак. Графік росту кількості вторгнень на протязі часу показано на рис. 1.
Методика розрахунку надійності комп'ютерних мереж
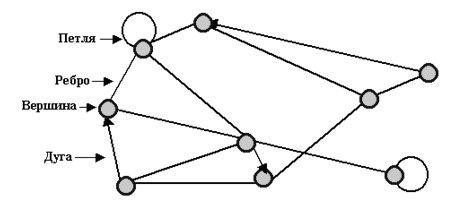
Для аналізу структурної надійності мереж зручно використовувати матрично-топологічні методи. В їхній основі лежить подання мережі за допомогою графа мережі (рис.1). Комп'ютерну мережу можна представити як сукупність множини X={x1,x2, ...,x} вузлів і множини U={uij } з'єднуючі вузли xi і xj ребер.
рис.1 Граф мережі
Будемо використовувати наступні основні поняття і визначення. Множина всіх вузлів графа G, суміжних з деяким вузлом xi, називається оточенням вузла xi і позначається N(xi). Ступінь вузла графа дорівнює числу ребер, інцидентних даному вузлу. Будемо позначати ступінь вузла х через deg(x). Послідовність, вузлів і ребер x1, u1, x2, u2…,xl, ul, xl+1називається маршрутом, що з'єднує вузли xl і xl+1, або (xl, xl+1)-маршрутом. Очевидно, що маршрут можна задати послідовністю x1, x2, …,xl+1 його вузлів, а також послідовністю u1, u2, …, ul ребер. Сама непересічна впорядкована послідовність ребер з вузла xs у вузол xt називається шляхом. Число ребер, що утворюють шлях називається рангом шляху. Між будь-якими двома вузлами мережі можна побудувати, як правило, множину шляхів. Шляхи називаються незалежними, якщо в них немає загальних ребер. Якщо між будь-якими двома вузлами існує не менш k незалежних шляхів, то мережа називається k-зв'язковою. Перетином мережі будемо називати мінімальну сукупність ребер, видалення яких розділить мережу на дві підмережі. Кількість ребер перетину називається рангом перетину. Перетини називаються незалежними, якщо вони не містять ті самі ребра. Нехай P1l – деякий шлях виду x1, x2, …,xl у графі G, xi і xj – вхідні в нього вузли, i < j. Очевидно, що частина xi, xi+1,…,xj шляхи P1l, що починається у вузлі xi і закінчується в xj, сама є шляхом графа G. Цей шлях будемо називати (xi, xj) – фрагментом шляху P1l.
Через відсутність прийнятної моделі механізму втрат в мережі і властивій складності розрахунку мережної надійності використовуються часові моделі з дискретною ймовірністю. Тут ми розглянемо найбільш популярну модель. В ній передбачається, що мережні компоненти (вузли і ребра мовою графів) можуть приймати лише два стани: працює або не працює. Стан мережного компонента - випадкова величина, що не залежить від стану інших компонентів (в загальному випадку це може бути і не так). Постановка задачі обчислення надійності: для кожного компонента мережі задана ймовірність того, що він перебуває в робочому стані, і потрібно обчислити міру надійності мережі.
В цьому випадку як показник надійності мережі в цілому можна використовувати ймовірність настання складної події, що полягає у встановленні зв'язків між всіма вузлами із заданої множини, і розраховувати його як відношення суми зважених коефіцієнтів важливості ймовірностей з'єднань пари вузлів.
де H0 – показник надійності всієї мережі, Кi – коефіцієнт важливості i-го з'єднання вузлів (0 Ki 1), Hi – показник надійності i-го з'єднання вузлів.
При проектуванні реальних мереж звичайно відсутня необхідність точного розрахунку надійності мережі. Проектувальникам необхідно лише переконатися в тім, що надійність мережі, з одного боку, не нижче заданої та, з іншого боку, не має економічно необґрунтованого запасу. Інакше кажучи, на практиці досить гарантувати, що дійсне значення надійності H0 перебуває в деяких межах Нтin < Н0 < Нтах. Оцінка надійності мережі із заданою кінцевою точністю дозволить скоротити трудомісткість розрахунків в тим більшій мірі, чим нижче необхідна точність оцінки. Існує методика розрахунку оцінок надійності, причому нижня оцінка Hμ розраховується по сукупності всіх шляхів між вузлами, верхня ж Hσ – по сукупності перетинів. При розрахунку надійності по сукупності шляхів додавання кожного наступного шляху приводить до збільшення надійності, а при розрахунку по сукупності перетинів додавання кожного наступного перетину приводить до зменшення структурної надійності, що створює передумови для двосторонньої оцінки структурної надійності з гарантованою точністю по обмежених наборах шляхів і перетинів. Ця властивість дозволяє регулювати трудомісткість оцінок надійності залежно від заданої точності.
Дійсно, для вирішення задачі досить послідовно переглядати шляхи μ, поки не виконається умова Hμ(m) ≥ Hmin і потім переглядати перетини σ, поки не виконається умова Hσ(r) ≤ Hmax. Тут m, r – число шляхів і перетинів відповідно. Якщо для деякого т виявиться, що Hμ(m) > Hmax, то можна припинити розрахунки і прийняти рішення, що в мережі закладена зайва надмірність, а якщо для деякого r виявиться, що Hσ(r) < Hmin , то це значить, що вимоги до надійності мережі не виконуються. Кількість потребуючого перегляду шляхів т і перетинів r звичайно набагато менше загального числа шляхів n і загального числа перетинів k графа, чим і досягається скорочення трудомісткості оцінки. Одночасно гарантується, що значення показника надійності мережі лежить в заданих межах Hμ(m) < H0 < Hσ(r) .
В такий спосіб для виконання розрахунків необхідний список всіх можливих шляхів і перетинів між заданими вузлами xa і xb. З літератури відомо, що шукана надійність з'єднання Нab залежить від надійності кожного шляху і варіантів їхніх перетинів по загальних ребрах. Якщо враховувати тільки незалежні шляхи, то трудомісткість обчислень значно скорочується. Аналогічна ситуація з незалежними перетинами. Нехай надійність j-го ребра i-го шляху - . Тоді надійність i-го шляху буде дорівнювати:
де mi -ранг шляху.
Якщо всі шляхи незалежні, то ймовірність зв’язності вузлів xa і xb по множині незалежних шляхів можна визначити як
де n – кількість незалежних шляхів між xa і xb.
Оскільки для підвищення точності оцінки необхідно максимізувати , то необхідно максимізувати число незалежних шляхів при одночасній мінімізації їхніх рангів.
Міркуючи аналогічно, неважко встановити, що для збільшення точності верхньої оцінки ймовірності зв’язаності вузлів по множині незалежних перетинів потрібно максимізувати число незалежних перетинів при мінімізації їхніх рангів. Проблема мережної надійності досліджується досить давно. В цей час ясно, що точного рішення навіть для мереж обмеженого розміру ця задача не має. Але можна вже сьогодні, якщо потрібно, зробити оцінку надійності зверху і знизу. Треба, втім, мати на увазі, що навіть це вимагає досить складних розрахунків.