Відмінності між версіями «Функції Беселя цілого порядку»
| (не показані 8 проміжних версій 2 учасників) | |||
| Рядок 1: | Рядок 1: | ||
| − | Рівняння Бесселя виникає під час знаходження рішень рівняння Лапласа і рівняння Гельмгольца в циліндрових і сферичних координатах. Тому функції Бесселя застосовуються при рішенні багатьох задач про розповсюдження хвиль, статичні потенціали тощо, наприклад: | + | '''<font color='Blue' size=3>Рівняння Бесселя </font>''' виникає під час знаходження рішень рівняння Лапласа і рівняння Гельмгольца в циліндрових і сферичних координатах. Тому функції Бесселя застосовуються при рішенні багатьох задач про розповсюдження хвиль, статичні потенціали тощо, наприклад: |
електромагнітні хвилі в циліндровому хвилеводі; | електромагнітні хвилі в циліндровому хвилеводі; | ||
| Рядок 12: | Рядок 12: | ||
| − | '''<font color=' | + | '''<font color='Salmon' size=3>Функції Бесселя цілого порядку. </font>''' |
Функція Бесселя невід'ємного цілого порядку можна отримати як коефіцієнти розвинення в ряд по додатних та від'ємних степенях змінної S функції <math>{e^{\frac{z}{2}(s-\frac{1}{s})}}</math>(ряд Лорана) | Функція Бесселя невід'ємного цілого порядку можна отримати як коефіцієнти розвинення в ряд по додатних та від'ємних степенях змінної S функції <math>{e^{\frac{z}{2}(s-\frac{1}{s})}}</math>(ряд Лорана) | ||
| − | <math>{e^{\frac{z}{2}(s-\frac{1}{s})}}={J_{0}(z)} | + | <math>{e^{\frac{z}{2}(s-\frac{1}{s})}}={J_{0}(z)}+\sum^{\infty}_{m=1}(S^m+(-S)^{-m})^{e^{\frac{z}{2}(s-\frac{1}{s})}}{J_{m}(z)} </math> |
| − | або <math>{\cos(z\mathrm{sin}\, t)={J_{0}(z)}+2\sum^{\infty}_{k=1}{J_{2k}(z)}\mathrm{cos}\, kt}</math> | + | або як коефіціент рядів Фур'є: |
| + | |||
| + | <math>{\cos(z\mathrm{sin}\, t)={J_{0}(z)}+2\sum^{\infty}_{k=1}{J_{2k}(z)}\mathrm{cos}\, kt}</math> | ||
<math>{\sin(z\mathrm{sin}\, t)=2\sum^{\infty}_{k=1}{J_{2k-1}(z)}\sin{(2k-1)}t}</math> | <math>{\sin(z\mathrm{sin}\, t)=2\sum^{\infty}_{k=1}{J_{2k-1}(z)}\sin{(2k-1)}t}</math> | ||
| − | або <math>{e\pm{iz\mathrm{sin}\, t}=\sum^{\infty}_{m=\infty}{J_{m}(z)}e^{- | + | або <math>{e^{\pm{iz\mathrm{sin}}\, t}=\sum^{\infty}_{m=\infty}{J_{m}(z)}e^{-imt}}</math> |
Часткові випадки:<math>{1={J_{0}(z)}+2\sum^{\infty}_{k=1}{J_{2k}(z)}}</math> | Часткові випадки:<math>{1={J_{0}(z)}+2\sum^{\infty}_{k=1}{J_{2k}(z)}}</math> | ||
| − | <math>{z^n=2^n\sum^{\infty}_{k=0}\frac{(m+2k)(n+k-1)}{k!}}</math> | + | <math>{z^n=2^n\sum^{\infty}_{k=0}\frac{(m+2k)(n+k-1)}{k!}{J_{2k+n}}}</math> |
Z беретьсь з множини комплексних чисел. | Z беретьсь з множини комплексних чисел. | ||
| + | |||
| + | [[Файл:600px-BesselJ_plot.svg.png]] '''<font color='Blue' size=3>Бесселя першого роду</font>''' <math>{J_{m}(x)}</math> | ||
| + | |||
| + | |||
| + | [[Файл:BesselY_plot.svg.png]] '<font color='Blue' size=3>Неймана </font>''' <math>{N_{m}(x)}</math> | ||
| + | |||
| + | |||
'''<font color='red' size=3>Умови ортогональності функції Бесселя. </font>''' | '''<font color='red' size=3>Умови ортогональності функції Бесселя. </font>''' | ||
| − | Нехай є нулі <math>{\ | + | Нехай є нулі <math>{\mu_{i}}</math> і <math>{\mu_{k}}</math> функції Бесселя <math>{{J_{m}(x)}}</math>. |
| − | Тоді <math>{\int_0^1{J_{m}}(\ | + | Тоді <math>{\int_0^1{J_{m}}(\mu_{i}x){S_{m}}(\mu_{k}x)tdx:=\begin{cases} 0, \mbox{i}\neq{k} \\ \frac{1}{2}{J^2_{m+1}}({\mu{i}}),i=k, \end{cases}}</math> |
| + | |||
| + | Ряд Фур'є-Бесселя для довільної функції <math>{f(x)}</math> на [0,1] мае вигляд:<math>{f(x)\thicksim \sum^{\infty}_{k=1}{a}{k}{J_{m}}(\mu_{k}x)}</math>. | ||
| + | |||
| + | <math>{{a}{k}=\frac{2}{{J_{m+1}}(\mu_{k})}\int_1^t{t}{f}(x){J_{m}}(\mu_{k}{t})dt}</math>. | ||
| + | |||
| + | |||
| + | [http://alglib.sources.ru/specialfunctions/bessel.php ALGLIB] | ||
| + | |||
| − | + | [[category: Вибрані статті з математичного аналізу]] | |
Поточна версія на 07:22, 21 травня 2010
Рівняння Бесселя виникає під час знаходження рішень рівняння Лапласа і рівняння Гельмгольца в циліндрових і сферичних координатах. Тому функції Бесселя застосовуються при рішенні багатьох задач про розповсюдження хвиль, статичні потенціали тощо, наприклад:
електромагнітні хвилі в циліндровому хвилеводі;
-теплопровідність в циліндрових об'єктах;
-форми коливання тонкої круглої мембрани
-швидкість частинок в циліндрі, що заповнена рідиною і обертається навколо своєї осі.
Функції Бесселя застосовуються і в рішенні інших задач, наприклад, при обробці сигналів.
Функції Бесселя цілого порядку.
Функція Бесселя невід'ємного цілого порядку можна отримати як коефіцієнти розвинення в ряд по додатних та від'ємних степенях змінної S функції Неможливо розібрати вираз (невідома помилка): {e^{\frac{z}{2}(s-\frac{1}{s})}} (ряд Лорана)
Неможливо розібрати вираз (невідома помилка): {e^{\frac{z}{2}(s-\frac{1}{s})}}={J_{0}(z)}+\sum^{\infty}_{m=1}(S^m+(-S)^{-m})^{e^{\frac{z}{2}(s-\frac{1}{s})}}{J_{m}(z)}
або як коефіціент рядів Фур'є:
Неможливо розібрати вираз (невідома помилка): {\cos(z\mathrm{sin}\, t)={J_{0}(z)}+2\sum^{\infty}_{k=1}{J_{2k}(z)}\mathrm{cos}\, kt}
Неможливо розібрати вираз (невідома помилка): {\sin(z\mathrm{sin}\, t)=2\sum^{\infty}_{k=1}{J_{2k-1}(z)}\sin{(2k-1)}t}
або Неможливо розібрати вираз (невідома помилка): {e^{\pm{iz\mathrm{sin}}\, t}=\sum^{\infty}_{m=\infty}{J_{m}(z)}e^{-imt}}
Часткові випадки:Неможливо розібрати вираз (невідома помилка): {1={J_{0}(z)}+2\sum^{\infty}_{k=1}{J_{2k}(z)}}
Неможливо розібрати вираз (невідома помилка): {z^n=2^n\sum^{\infty}_{k=0}\frac{(m+2k)(n+k-1)}{k!}{J_{2k+n}}}
Z беретьсь з множини комплексних чисел.
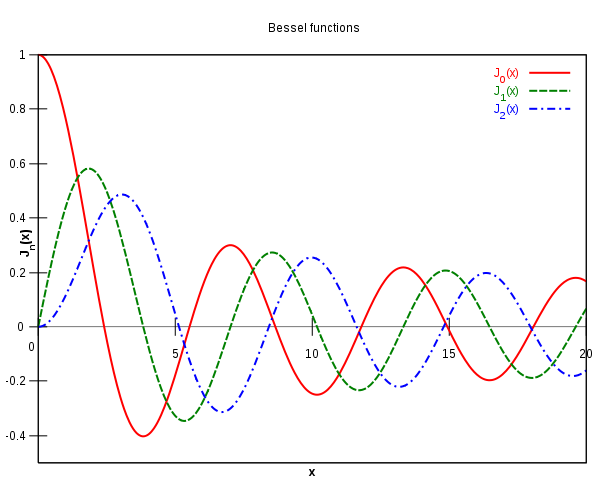Бесселя першого роду Неможливо розібрати вираз (невідома помилка): {J_{m}(x)}
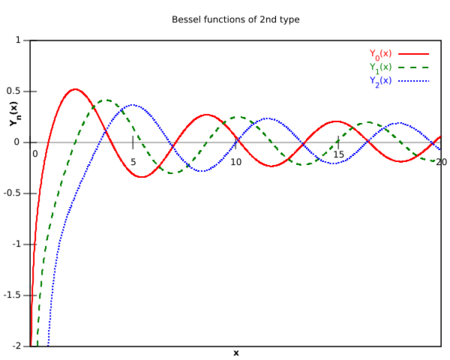'Неймана Неможливо розібрати вираз (невідома помилка): {N_{m}(x)}
Умови ортогональності функції Бесселя.
Нехай є нулі Неможливо розібрати вираз (невідома помилка): {\mu_{i}}
і Неможливо розібрати вираз (невідома помилка): {\mu_{k}}
функції Бесселя Неможливо розібрати вираз (невідома помилка): {{J_{m}(x)}}
. Тоді Неможливо розібрати вираз (невідома помилка): {\int_0^1{J_{m}}(\mu_{i}x){S_{m}}(\mu_{k}x)tdx:=\begin{cases} 0, \mbox{i}\neq{k} \\ \frac{1}{2}{J^2_{m+1}}({\mu{i}}),i=k, \end{cases}}
Ряд Фур'є-Бесселя для довільної функції Неможливо розібрати вираз (невідома помилка): {f(x)}
на [0,1] мае вигляд:Неможливо розібрати вираз (невідома помилка): {f(x)\thicksim \sum^{\infty}_{k=1}{a}{k}{J_{m}}(\mu_{k}x)}
.
Неможливо розібрати вираз (невідома помилка): {{a}{k}=\frac{2}{{J_{m+1}}(\mu_{k})}\int_1^t{t}{f}(x){J_{m}}(\mu_{k}{t})dt} .
