Відмінності між версіями «Циліндричні функції»
Матеріал з Вікі ЦДУ
| (не показано 19 проміжних версій цього учасника) | |||
| Рядок 2: | Рядок 2: | ||
:<math>{J_{m}(z)}=\int_0^\infty {e}^{-t}{t}^{z+1}dt\Rightarrow {I_m(z)}=(\frac{z}{2})^m\sum^{\infty}_{k=1}\frac{(-1)^k}{k!J(m+k+1)} </math> | :<math>{J_{m}(z)}=\int_0^\infty {e}^{-t}{t}^{z+1}dt\Rightarrow {I_m(z)}=(\frac{z}{2})^m\sum^{\infty}_{k=1}\frac{(-1)^k}{k!J(m+k+1)} </math> | ||
:Ще однією циліндричною функцією( розв'язком рівняння Бесcеля) є функція Бесcеля I роду | :Ще однією циліндричною функцією( розв'язком рівняння Бесcеля) є функція Бесcеля I роду | ||
| − | + | ==Функція Неймана (або Бесcеля I роду):== | |
:<math>{N_m(z)}=\frac{1}{sinm\pi}[J_m(z)cos\pi-J_{-m}(z)]</math> якщо <math>m \not\in \mathbf{Z}</math> | :<math>{N_m(z)}=\frac{1}{sinm\pi}[J_m(z)cos\pi-J_{-m}(z)]</math> якщо <math>m \not\in \mathbf{Z}</math> | ||
:<math>{N_m(z)}={(-1)}^mN_{-m}(z)=\frac{2}{\pi}J_m(z)(\ln\frac{z}{2}+c)-\frac{1}{\pi}(\frac{z}{2})^m\sum^{\infty}_{k=1}\frac{(-1)^k}{k!(m+k)!}(\frac{z}{2})^2k(\sum^{k}_{i=1}\frac{1}{i}+\sum^{m+k}_{i=1}{\frac{1}{i}})-{\frac{1}{\pi}}{(\frac{z}{2})^{-m}}\sum^{m-1}_{k=0}\frac{(m-k-1)!}{k!}(\frac{z}{2})^2k</math> | :<math>{N_m(z)}={(-1)}^mN_{-m}(z)=\frac{2}{\pi}J_m(z)(\ln\frac{z}{2}+c)-\frac{1}{\pi}(\frac{z}{2})^m\sum^{\infty}_{k=1}\frac{(-1)^k}{k!(m+k)!}(\frac{z}{2})^2k(\sum^{k}_{i=1}\frac{1}{i}+\sum^{m+k}_{i=1}{\frac{1}{i}})-{\frac{1}{\pi}}{(\frac{z}{2})^{-m}}\sum^{m-1}_{k=0}\frac{(m-k-1)!}{k!}(\frac{z}{2})^2k</math> | ||
| − | :якщо <math>m \not\in \mathbf{Z}</math> <math>c=-\int_0^\infty {e}^{-t}lntdt=0.577216</math>, с - стала Ейлера-Маскероні. | + | :якщо <math>m \not\in \mathbf{Z}</math> <math>c=-\int_0^\infty {e}^{-t}lntdt=0.577216</math>, '''<font color='green'> с - стала Ейлера-Маскероні.</font>''' |
| − | + | ||
| − | : Функція Генкеля I роду: | + | ==='''<font color='blue' size=3> На основі функцій Бесcеля I та II роду можна побудувати іншу пару циліндричних функцій</font>'''=== |
| + | |||
| + | :Функція Генкеля I роду: | ||
:<math>{H_m}^{(1)}(z)=J_{m}(z)+iN_{m}(z)</math> | :<math>{H_m}^{(1)}(z)=J_{m}(z)+iN_{m}(z)</math> | ||
| − | : Функція Генкеля II роду: | + | :Функція Генкеля II роду: |
:<math>{H_m}^{(2)}(z)=J_{m}(z)-iN_{m}(z)</math> | :<math>{H_m}^{(2)}(z)=J_{m}(z)-iN_{m}(z)</math> | ||
:Кожна циліндрична функція <math>~{Z_{m}(z)}</math> порядку m може бути представлена як лінійна комбінація <math>~J_{m}(k)</math> та <math>~N_{m}(k)</math> або лінійними комбінаціями :<math>{H_m}^{(1)}(z)</math> та <math>{H_m}^{(2)}(z)</math> | :Кожна циліндрична функція <math>~{Z_{m}(z)}</math> порядку m може бути представлена як лінійна комбінація <math>~J_{m}(k)</math> та <math>~N_{m}(k)</math> або лінійними комбінаціями :<math>{H_m}^{(1)}(z)</math> та <math>{H_m}^{(2)}(z)</math> | ||
| Рядок 17: | Рядок 19: | ||
:<math>~W({H_m}^{(1)}(z),{H_m}^{(2)}(z))=-\frac{4i}{z\pi} </math> | :<math>~W({H_m}^{(1)}(z),{H_m}^{(2)}(z))=-\frac{4i}{z\pi} </math> | ||
:<math>~W(J_{m}(z),J_{-m}(z))=\frac{-2sinm\pi}{z\pi} </math> при <math>m \in \mathbf{Z}, W=0, J_{m} і J_{-m} - </math>лінійно залежні | :<math>~W(J_{m}(z),J_{-m}(z))=\frac{-2sinm\pi}{z\pi} </math> при <math>m \in \mathbf{Z}, W=0, J_{m} і J_{-m} - </math>лінійно залежні | ||
| − | + | ||
| + | =='''<font color='blue'> Рекурентні співвідношення між функціями Бесселя:</font>'''== | ||
| + | |||
:<math>~Z_{m+1}(z)=\frac{Z_{m}}{z}Z_{m}(z)-Z_{m-1}(z)=</math>(відсутні похідні) <math>~=\frac{m}{z}Z_{m}(z)-\frac{d}{dz}Z_{m}(z)={-z}^m\frac{d}{dz}({z}^{-m}Z_{m}(z)) </math> | :<math>~Z_{m+1}(z)=\frac{Z_{m}}{z}Z_{m}(z)-Z_{m-1}(z)=</math>(відсутні похідні) <math>~=\frac{m}{z}Z_{m}(z)-\frac{d}{dz}Z_{m}(z)={-z}^m\frac{d}{dz}({z}^{-m}Z_{m}(z)) </math> | ||
| − | + | ||
| + | =='''<font color='blue'> Циліндричні функції, порядок яких дорівнює половині непарного цілого числа, виражаються через елементарні функції </font>'''== | ||
| + | |||
:<math>~{J_{\frac{1}{2}}(z)}=\sqrt{\frac{2}{\pi}}\frac{sinz}{\sqrt{z}}</math> | :<math>~{J_{\frac{1}{2}}(z)}=\sqrt{\frac{2}{\pi}}\frac{sinz}{\sqrt{z}}</math> | ||
:<math>~{J_{-{\frac{1}{2}}}(z)}=\sqrt{\frac{2}{\pi}}\frac{cosz}{\sqrt{z}}</math> | :<math>~{J_{-{\frac{1}{2}}}(z)}=\sqrt{\frac{2}{\pi}}\frac{cosz}{\sqrt{z}}</math> | ||
| Рядок 29: | Рядок 35: | ||
:<math>~{H_{\frac{1}{2}}^{(2)}(z)}=-\sqrt{\frac{2}{\pi}}\frac{1}{i}\frac{e^{-iz}}{\sqrt{z}}</math> | :<math>~{H_{\frac{1}{2}}^{(2)}(z)}=-\sqrt{\frac{2}{\pi}}\frac{1}{i}\frac{e^{-iz}}{\sqrt{z}}</math> | ||
:<math>~{H_{\frac{1}{2}}^{(2)}(z)}=\sqrt{\frac{2}{\pi}}\frac{e^{-iz}}{\sqrt{z}}</math> | :<math>~{H_{\frac{1}{2}}^{(2)}(z)}=\sqrt{\frac{2}{\pi}}\frac{e^{-iz}}{\sqrt{z}}</math> | ||
| + | |||
| + | =='''<font color='blue'> Інтегральні представлення функції Бесселя </font>'''== | ||
| + | |||
| + | :<math>~{J_{m}(z)}=\frac{1}{\pi}\int_0^{\frac{\pi}{2}} cos(mt-zsint)dt</math> <math>~m=0,1,2,...</math> | ||
| + | :<math>~{J_{2m}(z)}=\frac{2}{\pi}\int_0^{\frac{\pi}{2}} cos(zsint)cos2mtdt</math> <math>~m=0,1,2,...</math> | ||
| + | :<math>~{J_{2m+1}(z)}=\frac{2}{\pi}\int_0^{\frac{\pi}{2}} sin(zsint)sin(2m+1)tdt</math> <math>~m=0,1,2,...</math> | ||
| + | :<math>~{J_{m}(z)}=\frac{(-1)^{m}}{\pi}\int_0^{\pi} e^{izcost}cosmtdt</math> <math>~m=0,1,2,...</math> | ||
| + | :<math>~{J_{m}(z)}=\frac{(1)^{m}}{2i\pi}(\frac{z}{2})^{m}\oint\limits t^{-t-1}e^{t-\frac{z{2}}{2t}}dt(|argz|<\pi)</math> <math>~m=0,1,2,...</math> | ||
| + | |||
| + | =='''<font color='blue'>Нулі циліндричних функцій </font>'''== | ||
| + | |||
| + | :1. Нулі циліндричних функцій прості, за виключенням, можливо,<math>~z=0</math>. Послідовні додатні або від'ємні дійсні нулі двох лінійних незалежних дійсних циліндричних функцій поряжка m чергуються; <math>~z=0</math> існує один можливий спільний нуль. | ||
| + | :2. Функція :<math>~{J_{m}(z)}</math> має нескінченне число дійсних нулів; для <math>~m>-1</math> всі її нулі дійсні. Для <math>~m=0, \frac{1}{2}, 1, \frac{3}{2}, 2,...u; n=1,2,...,J_{m}(z)uJ_{m+n}(z)</math> не мають спільних нулів. | ||
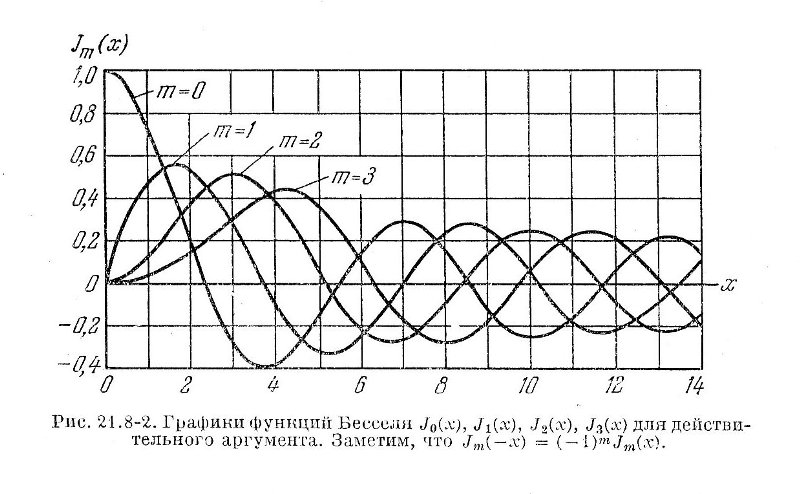
| + | [[Файл:Графіки функції Бесселя.jpg]] | ||
| + | |||
| + | Виконала: [[Користувач:Єсман Ірина Юріївна|Єсман Ірина Юріївна ]] | ||
| + | |||
| + | [[category: Вибрані статті з математичного аналізу]] | ||
Поточна версія на 21:32, 20 травня 2010
Циліндричними функціями - називається розвиток рівняння Бесcеля. У 17 пункті отримано першу циліндричну функцію - функція Бесcеля I роду у вигляді степеневого ряду. Цю функцію можна записати через γ-функцію:
- Неможливо розібрати вираз (невідома помилка): {J_{m}(z)}=\int_0^\infty {e}^{-t}{t}^{z+1}dt\Rightarrow {I_m(z)}=(\frac{z}{2})^m\sum^{\infty}_{k=1}\frac{(-1)^k}{k!J(m+k+1)}
- Ще однією циліндричною функцією( розв'язком рівняння Бесcеля) є функція Бесcеля I роду
Зміст
Функція Неймана (або Бесcеля I роду):
- Неможливо розібрати вираз (невідома помилка): {N_m(z)}=\frac{1}{sinm\pi}[J_m(z)cos\pi-J_{-m}(z)]
якщо Неможливо розібрати вираз (невідома помилка): m \not\in \mathbf{Z}
- Неможливо розібрати вираз (невідома помилка): {N_m(z)}={(-1)}^mN_{-m}(z)=\frac{2}{\pi}J_m(z)(\ln\frac{z}{2}+c)-\frac{1}{\pi}(\frac{z}{2})^m\sum^{\infty}_{k=1}\frac{(-1)^k}{k!(m+k)!}(\frac{z}{2})^2k(\sum^{k}_{i=1}\frac{1}{i}+\sum^{m+k}_{i=1}{\frac{1}{i}})-{\frac{1}{\pi}}{(\frac{z}{2})^{-m}}\sum^{m-1}_{k=0}\frac{(m-k-1)!}{k!}(\frac{z}{2})^2k
- якщо Неможливо розібрати вираз (невідома помилка): m \not\in \mathbf{Z}
Неможливо розібрати вираз (невідома помилка): c=-\int_0^\infty {e}^{-t}lntdt=0.577216
, с - стала Ейлера-Маскероні.
На основі функцій Бесcеля I та II роду можна побудувати іншу пару циліндричних функцій
- Функція Генкеля I роду:
- Неможливо розібрати вираз (невідома помилка): {H_m}^{(1)}(z)=J_{m}(z)+iN_{m}(z)
- Функція Генкеля II роду:
- Неможливо розібрати вираз (невідома помилка): {H_m}^{(2)}(z)=J_{m}(z)-iN_{m}(z)
- Кожна циліндрична функція Неможливо розібрати вираз (невідома помилка): ~{Z_{m}(z)}
порядку m може бути представлена як лінійна комбінація Неможливо розібрати вираз (невідома помилка): ~J_{m}(k)
та Неможливо розібрати вираз (невідома помилка): ~N_{m}(k)
або лінійними комбінаціями :Неможливо розібрати вираз (невідома помилка): {H_m}^{(1)}(z)
та Неможливо розібрати вираз (невідома помилка): {H_m}^{(2)}(z)
- Неможливо розібрати вираз (невідома помилка): ~Z_{m}(z)=aJ_{m}(z)+b\Nu_{m}(z)
- Неможливо розібрати вираз (невідома помилка): ~Z_{m}(z)=\alpha{H_m}^{(1)}(z)+\beta{H_m}^{(2)}(z)
Якобіан (визначник Вронського): Неможливо розібрати вираз (невідома помилка): ~W(J_{m}(z),N_m(z))=\frac{2}{z\pi}
- Неможливо розібрати вираз (невідома помилка): ~W({H_m}^{(1)}(z),{H_m}^{(2)}(z))=-\frac{4i}{z\pi}
- Неможливо розібрати вираз (невідома помилка): ~W(J_{m}(z),J_{-m}(z))=\frac{-2sinm\pi}{z\pi}
при Неможливо розібрати вираз (невідома помилка): m \in \mathbf{Z}, W=0, J_{m} і J_{-m} -
лінійно залежні
Рекурентні співвідношення між функціями Бесселя:
- Неможливо розібрати вираз (невідома помилка): ~Z_{m+1}(z)=\frac{Z_{m}}{z}Z_{m}(z)-Z_{m-1}(z)=
(відсутні похідні) Неможливо розібрати вираз (невідома помилка): ~=\frac{m}{z}Z_{m}(z)-\frac{d}{dz}Z_{m}(z)={-z}^m\frac{d}{dz}({z}^{-m}Z_{m}(z))
Циліндричні функції, порядок яких дорівнює половині непарного цілого числа, виражаються через елементарні функції
- Неможливо розібрати вираз (невідома помилка): ~{J_{\frac{1}{2}}(z)}=\sqrt{\frac{2}{\pi}}\frac{sinz}{\sqrt{z}}
- Неможливо розібрати вираз (невідома помилка): ~{J_{-{\frac{1}{2}}}(z)}=\sqrt{\frac{2}{\pi}}\frac{cosz}{\sqrt{z}}
- Неможливо розібрати вираз (невідома помилка): ~{J_{\frac{3}{2}}(z)}=\sqrt{\frac{2}{\pi}}(-\frac{cosz}{\sqrt{z}}+\frac{sinz}{z\sqrt{z}})
- Неможливо розібрати вираз (невідома помилка): ~{J_{-{\frac{3}{2}}}(z)}=\sqrt{\frac{2}{\pi}}(-\frac{sinz}{\sqrt{z}}-\frac{cosz}{z\sqrt{z}})
- Неможливо розібрати вираз (невідома помилка): ~{J_{k+\frac{1}{2}}(z)}=\sqrt{\frac{2}{\pi}}z^{k+\frac{1}{2}}(-\frac{1}{z}{\frac{d}{dz}})^{k}\frac{sint}{z}
Неможливо розібрати вираз (невідома помилка): ~(k=1,2,...)
- Неможливо розібрати вираз (невідома помилка): ~{H_{\frac{1}{2}}^{(1)}(z)}=\sqrt{\frac{2}{\pi}}\frac{1}{i}\frac{e^{iz}}{\sqrt{z}}
- Неможливо розібрати вираз (невідома помилка): ~{H_{-\frac{1}{2}}^{(1)}(z)}=\sqrt{\frac{2}{\pi}}\frac{e^{iz}}{\sqrt{z}}
- Неможливо розібрати вираз (невідома помилка): ~{H_{\frac{1}{2}}^{(2)}(z)}=-\sqrt{\frac{2}{\pi}}\frac{1}{i}\frac{e^{-iz}}{\sqrt{z}}
- Неможливо розібрати вираз (невідома помилка): ~{H_{\frac{1}{2}}^{(2)}(z)}=\sqrt{\frac{2}{\pi}}\frac{e^{-iz}}{\sqrt{z}}
Інтегральні представлення функції Бесселя
- Неможливо розібрати вираз (невідома помилка): ~{J_{m}(z)}=\frac{1}{\pi}\int_0^{\frac{\pi}{2}} cos(mt-zsint)dt
Неможливо розібрати вираз (невідома помилка): ~m=0,1,2,...
- Неможливо розібрати вираз (невідома помилка): ~{J_{2m}(z)}=\frac{2}{\pi}\int_0^{\frac{\pi}{2}} cos(zsint)cos2mtdt
Неможливо розібрати вираз (невідома помилка): ~m=0,1,2,...
- Неможливо розібрати вираз (невідома помилка): ~{J_{2m+1}(z)}=\frac{2}{\pi}\int_0^{\frac{\pi}{2}} sin(zsint)sin(2m+1)tdt
Неможливо розібрати вираз (невідома помилка): ~m=0,1,2,...
- Неможливо розібрати вираз (невідома помилка): ~{J_{m}(z)}=\frac{(-1)^{m}}{\pi}\int_0^{\pi} e^{izcost}cosmtdt
Неможливо розібрати вираз (невідома помилка): ~m=0,1,2,...
- Неможливо розібрати вираз (невідома помилка): ~{J_{m}(z)}=\frac{(1)^{m}}{2i\pi}(\frac{z}{2})^{m}\oint\limits t^{-t-1}e^{t-\frac{z{2}}{2t}}dt(|argz|<\pi)
Неможливо розібрати вираз (невідома помилка): ~m=0,1,2,...
Нулі циліндричних функцій
- 1. Нулі циліндричних функцій прості, за виключенням, можливо,Неможливо розібрати вираз (невідома помилка): ~z=0
. Послідовні додатні або від'ємні дійсні нулі двох лінійних незалежних дійсних циліндричних функцій поряжка m чергуються; Неможливо розібрати вираз (невідома помилка): ~z=0
існує один можливий спільний нуль.
- 2. Функція :Неможливо розібрати вираз (невідома помилка): ~{J_{m}(z)}
має нескінченне число дійсних нулів; для Неможливо розібрати вираз (невідома помилка): ~m>-1
всі її нулі дійсні. Для Неможливо розібрати вираз (невідома помилка): ~m=0, \frac{1}{2}, 1, \frac{3}{2}, 2,...u; n=1,2,...,J_{m}(z)uJ_{m+n}(z)
не мають спільних нулів.
Виконала: Єсман Ірина Юріївна