Відмінності між версіями «Стаття учня до проекту "Таємниці руху"»
| (не показано одну проміжну версію цього учасника) | |||
| Рядок 1: | Рядок 1: | ||
| − | + | [[Файл:25112.jpg|500px|праворуч]] | |
==Тема проекту: Таємниці руху== | ==Тема проекту: Таємниці руху== | ||
| Рядок 55: | Рядок 55: | ||
1. Возняк Г.М., Гусев В.А. Прикладные задачи на экстремумы. в курсе математики 4 – 8 классов: Пособие для учителей. – М.: Просвещение, 1985. – 144 с. | 1. Возняк Г.М., Гусев В.А. Прикладные задачи на экстремумы. в курсе математики 4 – 8 классов: Пособие для учителей. – М.: Просвещение, 1985. – 144 с. | ||
| + | |||
2. Коваленко В.Г. Дидактические игры на уроках математики. – М.: Просвещение, 1990. – 96 с. | 2. Коваленко В.Г. Дидактические игры на уроках математики. – М.: Просвещение, 1990. – 96 с. | ||
| + | |||
3. Розв’язування геометричних задач у середній школі / За ред. Л.М. Лоповка. – К.: Радянська школа, 1972. – 262 с. | 3. Розв’язування геометричних задач у середній школі / За ред. Л.М. Лоповка. – К.: Радянська школа, 1972. – 262 с. | ||
| + | |||
4. Математика. Точка Торичелли // http://math.hashcode.ru/questions/7197/геометрия-точка-торричелли | 4. Математика. Точка Торичелли // http://math.hashcode.ru/questions/7197/геометрия-точка-торричелли | ||
| + | |||
5. Задача 274. Изучение точек Торричелли // http://www.diofant.ru/problem/823/ | 5. Задача 274. Изучение точек Торричелли // http://www.diofant.ru/problem/823/ | ||
Поточна версія на 14:27, 30 січня 2015
Зміст
Тема проекту: Таємниці руху
Наша команда
"Математики": Софія Іванова, Микола Петренко, Ліля Синиця
Тема дослідження: Поворот
Проблема дослідження:
проектувальникам лінії зв'язку потрібно з'єднати пункти А, В і С. Як побудувати цю лінію, щоб витратити найменшу кількість кабелю?
Гіпотеза дослідження
Ми перефразували задачу наступним чином: потрібно всі три точки з'єднати відрізками так, щоб сума довжин всіх відрізків лінії зв’язку була найменшою.
Випадок 1. Якщо точки А, В і С лежать на одній прямій, то, зрозуміло, мінімальною лінією зв’язку буде відрізок, який з’єднує крайні точки.
Випадок 2. Точки А, В і С не лежать на одній прямій. Софія припустила, що мінімальною лінією зв’язку буде АВ+ВС+АС. У Миколи та Лілі виникли сумніви.
Мета дослідження
Результати дослідження
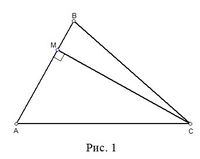
Ми розглянули найкоротшу відстань від точки С до АВ, тобто точку М, яка лежить на прямій АВ, причому СМ перпендикулярне АВ (рис.1). Тоді можна помітити, що АМ+ВМ+СМ<АВ+ВС+АС. Отже потрібно знайти таку точку М, щоб АМ+ВМ+СМ=min.
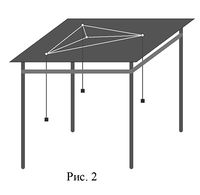
На допомогу нам прийшли фізики. На дерев’яному столі намалювали трикутник, просвердлили у вершинах дірочки, протягнули мотузки та зв’язали їх в одній точці над столом (рис. 2).
Прив’яжемо до вільних кінців гирьки однакової маси та відпустимо. Гирьки будуть намагатися опуститися якомога нижче (точніше, мінімізувати потенційну енергію системи трьох ваг). У найнижчому положенні сили врівноважать одна одну у внутрішній точці М трикутника або притягнуть точку М до однієї з вершин і будуть тягнути її «під стіл». Яка ж умова рівноваги у цьому випадку? Сума векторів однакової довжини дорівнює нулю тоді і тільки тоді, коли вони утворюють один з одним кути величиною 120°. Точку М у цьому випадку називають точкою Торрічеллі. Фізика підказала нам ідею розв’язування цієї задачі, але щоб знайти точку М, повернемося до геометрії. Розглянемо трикутник АВС. Нехай М – шукана точка, тоді АМ+ВМ+СМ=min. 1). Застосувавши поворот навколо точки А, отримаємо: точка В переходить в точку В1, точка М переходить в точку М1. Тоді АВ = АВ1, АМ = АМ1 = ММ1. Таким чином відрізок ВМ переходить у відрізок В1М1, тоді ВМ = В1М1. 2). Розглянемо АМ + ВМ + СМ = ММ1 + В1М1 +СМ ≥ В1С, тоді точки М і М1 належать відрізку В1С. 3). Застосувавши поворот навколо точки С, отримаємо: точка В переходить в точку В2, точка М переходить в точку М2. Тоді відрізок ВМ переходить у відрізок В2М2, тому ВМ = В2М2. 4). Таким чином, АМ + ВМ + СМ = АМ + В2М2 +ММ2 ≥ АВ2 точки М і М2 належать відрізку АВ2, отже відрізки В1С і АВ2 перетинаються в точці М.
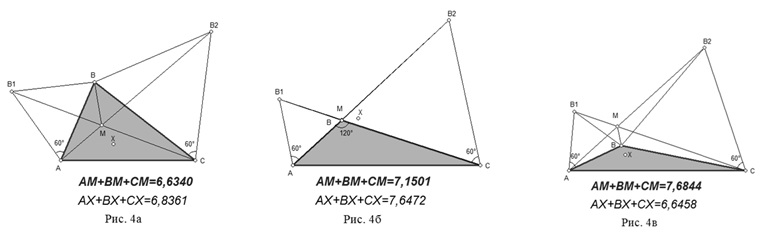
Виникає запитання: де буде знаходитися точка М, в залежності від величин кутів трикутника, тобто якщо: • кожен з кутів трикутника менший 120°; • один з кутів трикутника дорівнює 120°; • один з кутів трикутника більший від 120°.
Інформатики в програмному середовищі DG побудували динамічну модель до цієї задачі.
За допомогою цієї моделі ми разом дослідили кожен з випадків та зробили висновок:висновок, що коли у трикутника величина одного з кутів більша або дорівнює 120°, то точка Торрічеллі співпадає з вершиною цього кута.
Висновки
Ми впоралися з поставленим завданням завдяки згуртованій співпраці всередині нашої групи та з групами "Інформатики" і "Фізики".
Корисні ресурси
1. Возняк Г.М., Гусев В.А. Прикладные задачи на экстремумы. в курсе математики 4 – 8 классов: Пособие для учителей. – М.: Просвещение, 1985. – 144 с.
2. Коваленко В.Г. Дидактические игры на уроках математики. – М.: Просвещение, 1990. – 96 с.
3. Розв’язування геометричних задач у середній школі / За ред. Л.М. Лоповка. – К.: Радянська школа, 1972. – 262 с.
4. Математика. Точка Торичелли // http://math.hashcode.ru/questions/7197/геометрия-точка-торричелли
5. Задача 274. Изучение точек Торричелли // http://www.diofant.ru/problem/823/
Сторінка проекту Назва проекту
Кіровоградський державний педагогічний університет імені Володимира Винниченка