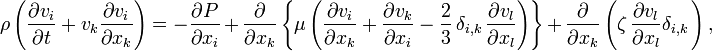Відмінності між версіями «Рівняння Нав'є-Стокса»
Serge (обговорення • внесок) (→Застосування) |
|||
| (не показана одна проміжна версія ще одного учасника) | |||
| Рядок 6: | Рядок 6: | ||
В векторному виді для нестисливої рідини вони записуються в такий спосіб: | В векторному виді для нестисливої рідини вони записуються в такий спосіб: | ||
| − | < | + | <br> |
[[Image:Riv1.png]] | [[Image:Riv1.png]] | ||
| Рядок 64: | Рядок 64: | ||
Варіації рівняння Нав'є - Стокса використовуються для опису руху повітряних мас атмосфери, зокрема , при формуванні прогнозу погоди. Для опису реальних течій у різних технічних пристроях прийнятну точність чисельного рішення можна одержати тільки при такій розрахунковій сітці, чарунки якої менше самого дрібного вихру. Це вимагає дуже великих витрат розрахункового часу на сучасних комп'ютерах. Тому були створені різні моделі турбулентності, що спрощують розрахунок реальних потоків. | Варіації рівняння Нав'є - Стокса використовуються для опису руху повітряних мас атмосфери, зокрема , при формуванні прогнозу погоди. Для опису реальних течій у різних технічних пристроях прийнятну точність чисельного рішення можна одержати тільки при такій розрахунковій сітці, чарунки якої менше самого дрібного вихру. Це вимагає дуже великих витрат розрахункового часу на сучасних комп'ютерах. Тому були створені різні моделі турбулентності, що спрощують розрахунок реальних потоків. | ||
<br> | <br> | ||
| − | |||
| − | |||
Поточна версія на 16:14, 20 травня 2010
Рівняння Нав'є́ — Сто́кса — система диференціальних рівнянь у частинних похідних, що описує рух і теплопередачу в'язкої н'ютонової рідини. Рівняння Нав'є-Стокса являються одними з найважливіших у гідродинаміці й застосовуються в математичному моделюванні багатьох природних явищ і технічних задач. Названі по імені французького фізика Луї Нав'є й британського математика Джорджа Стокса.
Система складається з двох рівнянь:
- рівняння руху,
- рівняння нерозривності.
В векторному виді для нестисливої рідини вони записуються в такий спосіб:
![]()
де ![]() — оператор Гамільтона, Δ — оператор Лапласа, t — час, ν — коефіцієнт кінематичної в'язкості, ρ — щільність, p — тиск,
— оператор Гамільтона, Δ — оператор Лапласа, t — час, ν — коефіцієнт кінематичної в'язкості, ρ — щільність, p — тиск, ![]() — векторне поле швидкостей,
— векторне поле швидкостей, ![]() — векторне поле масових сил. Невідомі p і V являються функціями часу t і координати
— векторне поле масових сил. Невідомі p і V являються функціями часу t і координати ![]() , де
, де ![]() , n = 2,3 — плоска або тривимірна область, у якій рухається рідина. Звичайно в систему рівнянь Нав'є́ — Стокса додають крайові й початкові умови, наприклад
, n = 2,3 — плоска або тривимірна область, у якій рухається рідина. Звичайно в систему рівнянь Нав'є́ — Стокса додають крайові й початкові умови, наприклад
Іноді в систему рівнянь Нав'є́ — Стокса додатково включають рівняння теплопровідності й рівняння стану.
При урахуванні стискальності рівняння Нав'є́ — Стокса приймає наступний вид:
де μ — коефіцієнт динамічної в'язкості, ζ — «друга в'язкість».
Аналіз та розв'язування рівнянь
В аналізі розв'язань рівнянь полягає суть однієї з відкритих проблем, за вирішення яких Математичний інститут Клея призначив премію в 1 млн доларів США. Необхідно довести або спростувати існування глобального гладкого рішення задачі Коші для тривимірних рівнянь Нав'є́ - Стокса. Знаходження загального розв'язання системи Нав'є́ - Стокса для просторового або плоского потоку ускладнюється тим, що воно нелінійне й сильно залежить від початкових і граничних умов.
Також ряд комерційних фірм, наприклад Боинг, призначили свої премії.
Дотепер розв'язання цих рівнянь знайдені лише в деяких окремих випадках. У цей час існує кілька ситуацій (обумовлених простою геометрією), які вирішені в аналітичному виді. В інших випадках використовується чисельне моделювання.
Деякі точні розв'язання:
- Стаціонарні течії в простих каналах (течія Пуазейля, течія Тейлора - Куетта та ін.)
- Солітони й нелінійні хвилі. Звичайний солітон може бути рішенням системи при дуже складних граничних умовах. Уперше він спостерігався експериментально в каналі інженером Худобою Расселом.
- Рішення, яке існує кінцевий час (так звані режими із загостренням, blow-up). Капнувши краплю на поверхню води, можна спостерігати сплеск, який існує кінцевий час, як і кільцевий вихор ядерного вибуху. Гіпотеза про це висунута Jean Leray в 1933 р. Він припустив, що в рідині турбулентність (хаос) утворюється завдяки утворенню точок або вихрової нитки, на якій деякий компонент швидкості стає нескінченною.
- Звукові коливання. При малій амплітуді хвиль вони також стають рішенням. Нелінійні члени рівняння можна відкинути, тому що вони не впливають на рішення. Рішенням є гармонійні функції синуса або косинуса, тобто звукові коливання, які ми чуємо.
Основні властивості системи Нав'є — Стокса
- При перевищенні числа Рейнольдса вище деякого критичного числа, аналітичне точне рішення для просторового або плоского потоку мають хаотичний вигляд (так звана турбулентність). В окремому випадку, воно пов'язане з теорією Фейгенбаума або іншими сценаріями перехід до хаосу. При зменшенні числа Рейнольдса нижче критичного, рішення знову приймає не хаотичний вид.
- Виняткова чутливість до зміни коефіцієнтів рівняння при турбулентному режимі: при зміні числа Re на 0,05 % рішення зовсім відрізняються друг від друга.
- Існує думка (Бударин В.А. Аналіз прихованих властивостей системи Нав'є - Стокса//Тез. докл. 6 Мінськ. межд.форум, ИТМО.- 2008 - т.1.- С.75-76), що дане рівняння являється наближеним. Це обґрунтовується використанням при виводі рівняння Нав'є - Стокса лінійного рівняння для знаходження тиску p, як функції його нелінійних компонентів. Така позиція говорить про існування різних значень числа Рейнольдса (для різних часткових задач), у межах якого лінійний закон осуреднення коректний.
Застосування
Одним із застосувань системи рівнянь Нав'є - Стокса являється опис течій у мантії Землі ("проблема динамо").
Варіації рівняння Нав'є - Стокса використовуються для опису руху повітряних мас атмосфери, зокрема , при формуванні прогнозу погоди. Для опису реальних течій у різних технічних пристроях прийнятну точність чисельного рішення можна одержати тільки при такій розрахунковій сітці, чарунки якої менше самого дрібного вихру. Це вимагає дуже великих витрат розрахункового часу на сучасних комп'ютерах. Тому були створені різні моделі турбулентності, що спрощують розрахунок реальних потоків.