|
|
| Рядок 1: |
Рядок 1: |
| − | | + | Типи алгоритмів |
| − | В алгоритмах команди записуються один за одним у певному порядку. Виконуються вони не обов'язково в записаній послідовності: залежно від порядку виконання команд можна виділити три типи алгоритмів:
| + | Призначення блоків випливає з їхніх назв. Блоки з’єднують лініями, які описують послідовність виконання команди. Ці лінії називаються лініями потоків передавання інформації. Природні напрями потоків зверху-вниз і зліва направо. Якщо напрямок потоку інший то лінія повинна мати стрілку. |
| | + | Типи алгоритмів |
| | + | Є 4-ри типи алгоритмів: |
| | + | -прості; |
| | + | -розгалужені; |
| | + | -циклічні; |
| | + | -універсальні; |
| | + | |
| | | | |
| − | • лінійні алгоритми;
| + | <center>'''Лінійні алгоритми (прості)'''</center> [[Файл:Bbb.jpg|350px|right]] |
| − | | + | |
| − | • алгоритми з розгалуженнями;
| + | |
| − | | + | |
| − | • алгоритми з повтореннями.
| + | |
| | | | |
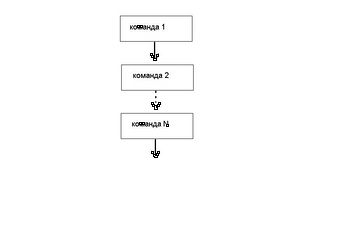
| | + | Алгоритм, у якому команди виконуються в порядку їх запису, тобто послідовно один за одним, називається лінійним. |
| | | | |
| | | | |
| − | <center>'''Лінійні алгоритми'''</center> [[Файл:Bbb.jpg|350px|right]]
| |
| − |
| |
| − |
| |
| − | Алгоритм, у якому команди виконуються в порядку їх запису, тобто послідовно один за одним, називається лінійним.
| |
| − |
| |
| − | Наприклад, лінійним є наступний алгоритм посадки дерева:
| |
| − |
| |
| − | 1) викопати в землі ямку;
| |
| − |
| |
| − | 2) вилучити в ямку саджанець;
| |
| − |
| |
| − | 3) засипати ямку із саджанцем землею;
| |
| − |
| |
| − | 4) полити саджанець водою.
| |
| − |
| |
| − |
| |
| | <center>'''Алгоритми з розгалуженнями'''</center> [[Файл:Iges.jpg|350px|right]] | | <center>'''Алгоритми з розгалуженнями'''</center> [[Файл:Iges.jpg|350px|right]] |
| | | | |
| − | Ситуації, коли заздалегідь відома послідовність необхідних дій, зустрічаються вкрай рідко. У житті часто доводиться ухвалювати рішення залежно від обстановки. Якщо йде дощ, ми беремо парасоль і надягаємо плащ; якщо пекуче, надягаємо легкий одяг. Зустрічаються й більш складні умови вибору, У деяких випадках від обраного рішення залежить подальша доля людини.
| |
| − |
| |
| − | Логікові ухвалення рішення можна описати так:
| |
| − |
| |
| − | ЯКЩО ТО ІНАКШЕ
| |
| − |
| |
| − | ''Приклади:''
| |
| − |
| |
| − | • ЯКЩО прагнеш бути здоровий, ТО загартовуйся, ІНАКШЕ валяйся весь день на дивані;
| |
| − |
| |
| − | • ЯКЩО низько ластівки літають, ТО буде дощ, ІНАКШЕ дощу не буде;
| |
| − |
| |
| − | • ЯКЩО уроки виучені, ТО йди гуляти, ІНАКШЕ вчи уроки.
| |
| − |
| |
| − | У деяких випадках можуть бути відсутні;
| |
| − |
| |
| − | ЯКЩО ТО
| |
| − |
| |
| − | ''Приклад:''
| |
| − |
| |
| − | • ЯКЩО назвався груздем, ТО полізай у кузов.
| |
| − |
| |
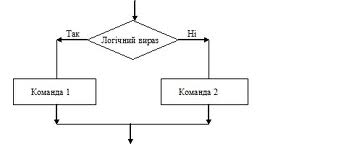
| − | Форма організації дій, при якій залежно від виконання деякої умови відбувається одна або інша послідовність кроків, називається розгалуженням.
| |
| − |
| |
| − | Зобразимо б виді блок-схеми послідовність дій учня 6 класу Мухіна Васі, яку він уявляє собі так: «Якщо Павлик будинку, будемо вирішувати завдання по математиці. А якщо ні, то слід подзвонити Марині й разом готовити доповідь по біології. Якщо ж Марини немає будинку, то треба сісти за твір.»
| |
| − |
| |
| − |
| |
| | | | |
| | <center>'''Алгоритми з повтореннями'''</center> [[Файл:Загруже.jpg|350px|right]] | | <center>'''Алгоритми з повтореннями'''</center> [[Файл:Загруже.jpg|350px|right]] |
| | + | |
| | | | |
| − |
| + | Універсальні алгоритми – це такі які містять в собі вище перечисленні такі алгоритми. |
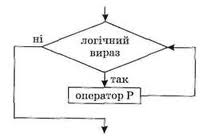
| − | На практиці часто зустрічаються завдання, у яких одне або кілька дій буває необхідно повторити кілька раз, поки дотримується деяке заздалегідь установлене умова.
| + | |
| − | | + | |
| − | Форма організації дій, при якій виконання однієї й тієї ж послідовності команд повторюється, поки виконується деяке заздалегідь установлене умова, називається циклом (повторенням).
| + | |
| − | | + | |
| − | Алгоритм, що містить цикли, називається циклічним алгоритмом або алгоритмом з повтореннями.
| + | |
| − | | + | |
| − | Ситуація, при якій виконання циклу ніколи не закінчується, називається зацикленням. Слід розробляти алгоритми, що не допускають таких ситуацій.
| + | |
| − | | + | |
| − | Розглянемо приклад з математики.
| + | |
| − | | + | |
| − | Натуральне число називають простим, якщо воно має тільки два дільники: одиницю й саме це число .
| + | |
| − | | + | |
| − | 2, 3, 5, 7 — прості числа; 4, 6, 8 — ні. В III столітті до нашої ери грецький математик Ератосфен запропонував наступний алгоритм для знаходження всіх простих чисел, менших заданого числа n;
| + | |
| − | | + | |
| − | 1) виписати всі натуральні числа від 1 до n;
| + | |
| − | | + | |
| − | 2) викреслити 1;
| + | |
| − | | + | |
| − | 3) підкреслити найменше з невідмічених чисел;
| + | |
| − | | + | |
| − | 4) викреслити всі числа, кратні підкресленому на попередньому кроці;
| + | |
| − | | + | |
| − | 5) якщо в списку є невідмічені числа, то перейти до кроку 3, а якщо ні, то всі підкреслені числа — прості.
| + | |
| − | | + | |
| − | Це циклічний алгоритм. При його виконанні повторення кроків 3-5 відбувається, поки у вихідному списку залишаються невідмічені числа.
| + | |
Алгоритм, у якому команди виконуються в порядку їх запису, тобто послідовно один за одним, називається лінійним.